Matlab主成分分析在社会科学中的应用：舆情分析与社会趋势预测的利器

# 1. 主成分分析（PCA）基础**

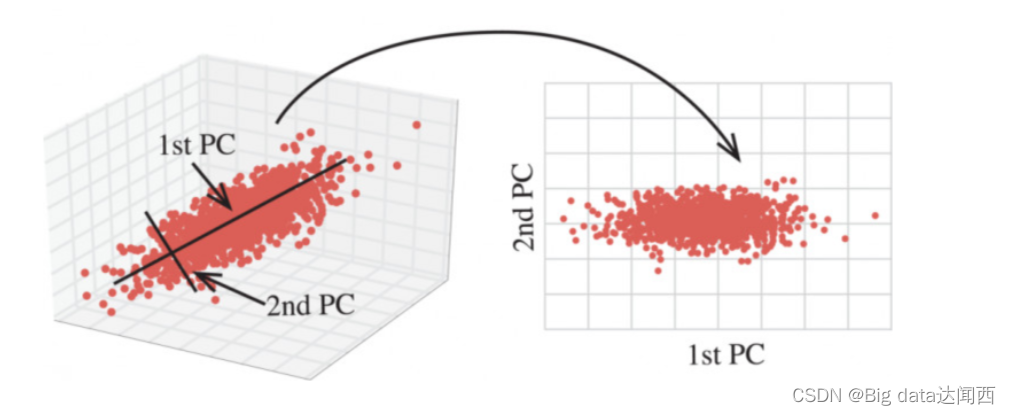
主成分分析（PCA）是一种降维技术，用于将高维数据投影到低维空间中，同时保留原始数据中的最大方差。PCA 的基本原理是通过线性变换将原始数据转换为一组正交基，这些基称为主成分。主成分的方差从最大到最小排列，前几个主成分通常包含了原始数据中大部分的信息。

PCA 算法的步骤如下：

1. 对原始数据进行中心化，即减去每个特征的均值。
2. 计算协方差矩阵或相关矩阵。
3. 对协方差矩阵或相关矩阵进行特征值分解。
4. 将特征值从大到小排序，并取前 k 个特征值对应的特征向量作为主成分。
5. 将原始数据投影到主成分上，得到降维后的数据。

# 2. PCA在舆情分析中的应用

PCA在舆情分析中发挥着至关重要的作用，它可以有效地对舆情数据进行降维和聚类，从而提取出舆情事件的关键特征和发展趋势。

### 2.1 舆情数据的预处理和特征提取

舆情数据通常包含大量文本信息，需要进行预处理和特征提取才能应用PCA进行降维和聚类。

#### 2.1.1 文本预处理技术

文本预处理是舆情分析中必不可少的步骤，它包括以下操作：

- **分词：**将文本中的句子和段落拆分为单个词语。
- **去停用词：**去除一些常见的无意义词语，如"的"、"了"等。
- **词干提取：**将词语还原为其基本形式，如"running"还原为"run"。
- **词性标注：**识别词语的词性，如名词、动词、形容词等。

#### 2.1.2 特征提取方法

特征提取是将预处理后的文本数据转换为适合PCA降维的数值特征的过程。常用的特征提取方法包括：

- **词频-逆向文档频率（TF-IDF）：**计算每个词语在文档中出现的频率和在整个语料库中出现的频率的比值，以衡量词语的重要性。
- **词嵌入：**将词语映射到一个高维向量空间中，每个维度代表词语的语义特征。
- **主题模型：**将文本数据分解为一系列主题，每个主题由一组相关的词语组成。

### 2.2 PCA在舆情分析中的降维和聚类

#### 2.2.1 PCA降维原理

PCA是一种线性降维技术，它通过寻找数据中方差最大的方向来将高维数据投影到低维空间中。在舆情分析中，PCA可以将高维的舆情特征数据投影到低维空间中，从而提取出舆情事件的关键特征和趋势。

#### 2.2.2 聚类算法在舆情分析中的应用

聚类算法可以将舆情数据中的相似样本分组到不同的簇中。在舆情分析中，聚类算法可以用于识别舆情事件的不同类型、发现舆论领袖和划分舆论阵营。

import numpy as np
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans

# 加载舆情数据
data = np.loadtxt("舆情数据.txt", delimiter=",")

# 应用PCA降维
pca = PCA(n_components=2)
data_reduced = pca.fit_transform(data)

# 应用KMeans聚类
kmeans = KMeans(n_clusters=3)
clust