揭开Matlab主成分分析与PCA的神秘面纱：降维算法大揭秘

# 1. Matlab主成分分析（PCA）简介

**1.1 PCA概述**

主成分分析（PCA）是一种广泛应用于降维和特征提取的统计技术。它通过线性变换将高维数据投影到低维空间，同时保留原始数据的最大方差。PCA在数据可视化、模式识别、数据压缩和异常检测等领域有着广泛的应用。

**1.2 PCA的优点**

PCA的主要优点包括：

* **降维：**PCA可以有效地减少数据维度，简化数据处理和分析。
* **特征提取：**PCA提取的数据主成分代表了原始数据的关键特征，可以用于特征选择和分类。
* **数据可视化：**PCA可以将高维数据投影到低维空间，便于数据可视化和模式识别。

# 2. PCA理论基础

### 2.1 降维与主成分分析

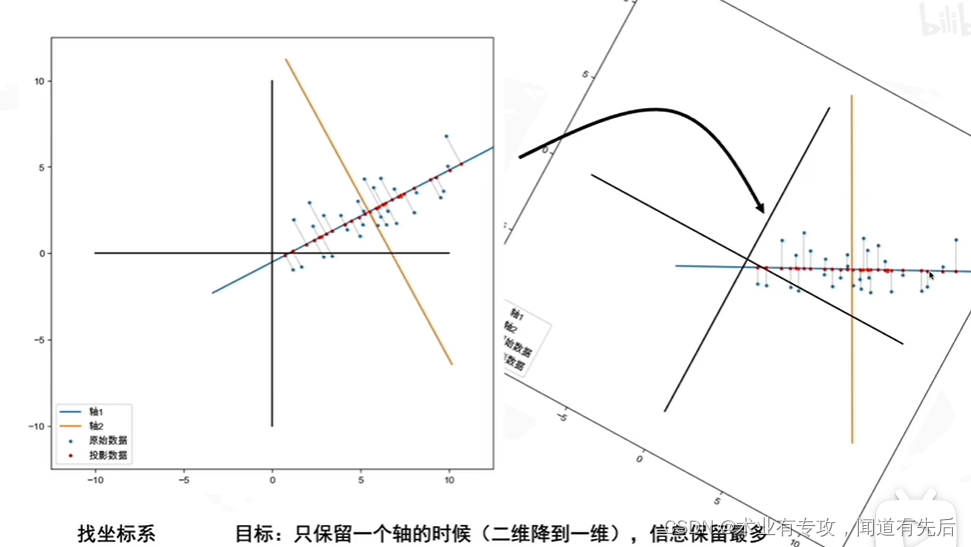
**降维**

降维是一种数据处理技术，其目的是将高维数据投影到低维空间中，同时保留原始数据中最重要的信息。降维可以减少数据的复杂性，提高计算效率，并改善数据的可视化。

**主成分分析（PCA）**

PCA是一种降维技术，它通过寻找数据中方差最大的方向来投影数据。这些方向称为主成分，它们代表了数据中最大的可变性。PCA的目标是将数据投影到由主成分构成的低维空间中，同时最大化投影数据的方差。

### 2.2 PCA算法原理

PCA算法的步骤如下：

1. **数据标准化：**对数据进行标准化，使其均值为0，方差为1。这确保了每个特征在PCA过程中具有相同的权重。
2. **计算协方差矩阵：**计算数据协方差矩阵，其中元素表示不同特征之间的协方差。
3. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. **选择主成分：**选择特征值最大的特征向量作为主成分。主成分的数量由所需的降维程度决定。
5. **数据投影：**将数据投影到由主成分构成的低维空间中。

### 2.3 PCA的数学表述

PCA的数学表述如下：

给定一个数据矩阵X，其维度为m x n，其中m为样本数，n为特征数。

**协方差矩阵：**

C = 1 / (m - 1) * X^T * X

**特征值分解：**

C * V = V * D

其中：

* C是协方差矩阵
* V是特征向量矩阵
* D是对角矩阵，包含特征值

**主成分：**

主成分是特征向量矩阵V中的列向量。

**数据投影：**

Y = X * V

其中：

* Y是投影后的数据
* X是原始数据
* V是特征向量矩阵

# 3.1 数据预处理与标准化

在进行PCA分析之前，数据预处理是至关重要的，它可以提高算法的准确性和鲁棒性。数据预处理主要包括以下步骤：

**1. 缺失值处理**

缺失值的存在会影响PCA的分析结果。对于缺失值，可以采用以下处理方法：

- **删除法：**直接删除包含缺失值的样本或特征。
- **插补法：**使用统计方法（如均值、中位数或众数）或机器学习方法（如k近邻）对缺失值进行插补。

**2. 异常值处理**

异常值是指与其他数据点明显不同的极端值。异常值的存在会扭曲PCA的结果。对于异常值，可以采用以下处理方法：

- **删除法：**直接删除异常值。
- **Winsorization：**将异常值替换为离散箱的边界值。
- **标准化：**将异常值缩放或转换到与其他数据点相同的范围内。

**3. 标准化**

标准化是将数据转换为具有相同均值和标准差的过程。标准化可以消除不同特征之间的量纲差异，使PCA算法能够公平地处理所有特征。

标准化的公式如下：

x_std = (x - mean(x)) / std(x)

其中：

- `x` 是原始数据
- `