Matlab主成分分析在能源领域的应用：能源需求预测与优化的利器

# 1. 主成分分析概述**

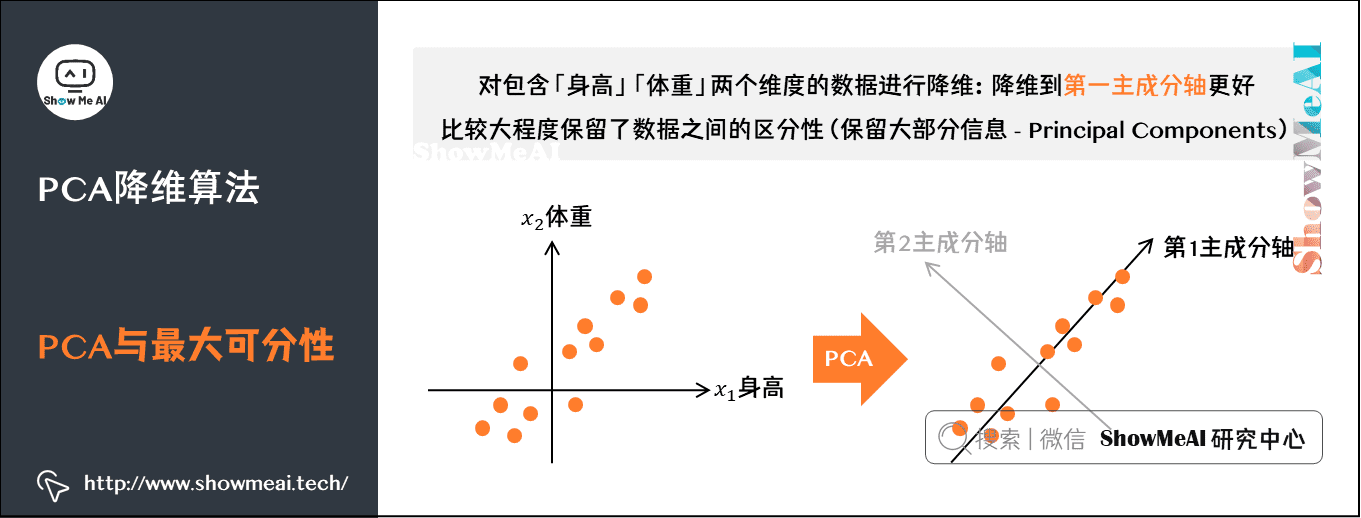
主成分分析（PCA）是一种统计技术，用于将高维数据降维，同时保留数据中的最大方差。它通过将原始变量线性组合成一组新的正交变量（主成分）来实现这一点，这些变量按方差从大到小排列。

PCA 的主要优点在于它可以简化数据，同时保留其最重要的特征。这使得它成为数据可视化、模式识别和预测建模的宝贵工具。在能源领域，PCA 已被广泛应用于需求预测、优化和资源评估等方面。

# 2. 主成分分析在能源需求预测中的应用

### 2.1 能源需求预测的挑战

能源需求预测对于能源规划、政策制定和投资决策至关重要。然而，能源需求预测面临着诸多挑战：

- **数据复杂性：**能源需求数据往往庞大且复杂，包含多种因素，如经济增长、人口变化、技术进步和天气条件。
- **非线性关系：**能源需求与影响因素之间通常存在非线性关系，这使得传统预测模型难以准确捕捉。
- **不确定性：**能源需求受多种不确定因素的影响，如经济波动、政策变化和自然灾害，这增加了预测的难度。

### 2.2 主成分分析在能源需求预测中的原理和方法

主成分分析（PCA）是一种降维技术，可以将高维数据转换为低维数据，同时保留原始数据的关键信息。在能源需求预测中，PCA可以用于：

- **识别关键影响因素：**PCA可以识别影响能源需求的主要变量，并将其组合成更少数量的主成分。
- **消除冗余：**PCA可以去除变量之间的冗余，简化预测模型，提高预测精度。
- **提高可解释性：**PCA产生的主成分往往具有物理意义，便于解释和分析。

PCA在能源需求预测中的应用步骤如下：

1. **数据预处理：**对能源需求数据进行标准化或归一化，确保变量具有可比性。
2. **协方差矩阵计算：**计算能源需求数据协方差矩阵，反映变量之间的相关性。
3. **特征值和特征向量分解：**对协方差矩阵进行特征值和特征向量分解，得到主成分。
4. **主成分选择：**根据特征值或累积方差贡献率，选择保留的主成分数量。
5. **预测模型构建：**使用主成分作为输入变量，构建预测模型，如回归模型或神经网络模型。

### 2.3 主成分分析在能源需求预测中的实践案例

**案例：中国能源需求预测**

研究人员使用PCA对中国2000-2019年的能源需求数据进行分析。结果表明，前三个主成分解释了85%以上的方差，反映了经济增长、人口变化和技术进步对能源需求的影响。基于主成分的预测模型比传统模型具有更高的精度和可解释性。

**代码块：**

import numpy as np
from sklearn.decomposition import PCA

# 数据预处理
data = pd.read_csv('energy_demand.csv')
data = (data - data.mean())