Matlab主成分分析在医学领域的应用：疾病诊断与预后分析的利器

# 1. Matlab主成分分析（PCA）概述

主成分分析（PCA）是一种广泛应用于数据分析和降维的统计技术。在Matlab中，可以使用`pca`函数进行PCA分析。`pca`函数的语法如下：

[coeff,score,latent,tsquared,explained,mu] = pca(X, 'NumComponents', n)

其中，`X`是输入数据矩阵，`n`指定要提取的主成分数。`coeff`是主成分系数，`score`是主成分得分，`latent`是主成分方差，`tsquared`是Hotelling's T²统计量，`explained`是主成分解释的方差百分比，`mu`是输入数据的均值。

# 2. PCA在医学领域的应用理论基础

### 2.1 PCA的数学原理和算法

**PCA的数学原理**

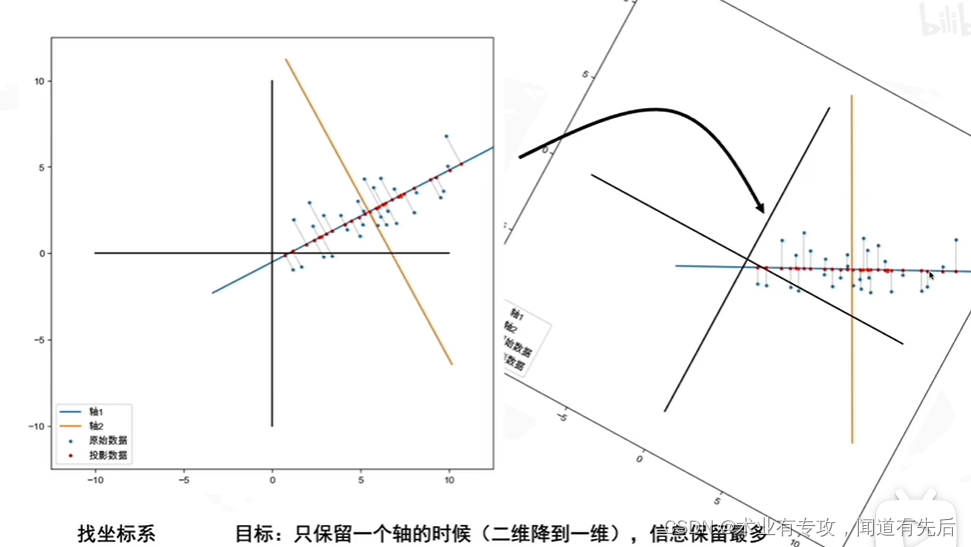
PCA是一种线性变换，将高维数据投影到低维空间中，同时最大化投影数据的方差。其数学原理如下：

设有n个样本，每个样本有m个特征，则原始数据矩阵X为n×m矩阵。PCA的目标是找到一个正交变换矩阵P，将X投影到k维子空间中，使得投影数据的方差最大化。

投影矩阵P的第i列对应于第i个主成分，主成分是原始特征的线性组合。主成分的方差等于投影数据在该主成分方向上的方差。

**PCA的算法**

PCA的算法主要分为以下步骤：

1. 对数据矩阵X进行中心化，即减去每个特征的均值。
2. 计算协方差矩阵C。
3. 对协方差矩阵C进行特征值分解，得到特征值λ和特征向量v。
4. 选择前k个特征值对应的特征向量，组成投影矩阵P。
5. 将原始数据X投影到子空间中，得到降维后的数据矩阵Y。

### 2.2 PCA在医学数据降维中的作用

PCA在医学数据降维中具有以下作用：

**数据可视化**

PCA可以将高维医学数据投影到低维空间中，方便可视化和分析。例如，在癌症研究中，PCA可以将高维基因表达数据投影到二维或三维空间中，帮助研究人员识别不同癌症类型的模式。

**特征提取**

PCA可以提取出数据中最重要的特征，这些特征可以用来构建分类或预测模型。例如，在疾病诊断中，PCA可以提取出与疾病相关的特征，帮助医生进行疾病分类和识别。

**降噪**

PCA可以去除数据中的噪声和冗余信息，提高数据的信噪比。例如，在医学影像分析中，PCA可以去除影像中的噪声，提高影像的质量。

**代码块：PCA降维示例**

import numpy as np
from sklearn.decomposition import PCA

# 原始数据矩阵
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 中心化数据
X_centered = X - np.mean(X, axis=0)

# 计算协方差矩阵
C = np.cov(X_centered)

# 特征值分解
eig_vals, eig_vecs = np.linalg.eig(C)

# 选择前2个主成分
P = eig_vecs[:, :2]

# 降维
X_reduced = np.dot(X_centered, P)

# 输出降维后的数据
print(X_reduced)

**逻辑分析：**

这段代码演示了PCA降维的过程。首先，将原始数据中心化，然后计算协方差矩阵。接着，对协方差矩阵进行特征值分解，得到特征值和特征向量。最后，选择前两个主成分对应的特征向量组成投影矩阵，并将原始数据投影到子空间中，得到降维后的数据。

# 3.1 疾病诊断中的数据预处理

在疾病诊断中，PCA的应用离不开数据预处理这一关键步骤。数据预处理的目的是将原始医学数据转化为适合PCA分析的格式，以提高分析的准确性和可靠性。