图数据结构与存储对Java最短路径算法的影响分析

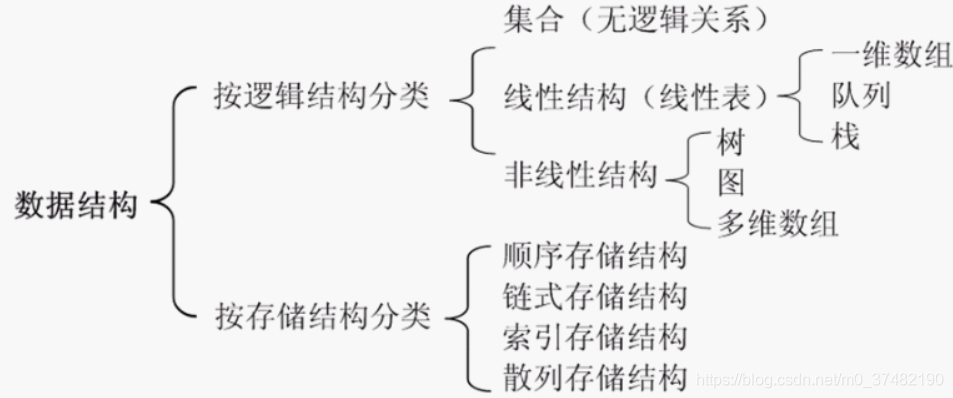
# 1. 图数据结构的基础知识

图是一种强大的数据结构，广泛应用于各种算法和数据组织中，特别适用于表示和处理网络和复杂关系。它由节点（或顶点）和边（或连接）组成，能够描述实体间的多种关系。

## 图的定义和术语

图（G）由两个集合组成：顶点的有限非空集合V(G)和顶点之间关系的边的集合E(G)。顶点通常用字母V表示，边用字母E表示。如果图中顶点之间存在边，则称这两个顶点是相邻的，与顶点V相邻的顶点集合称为V的邻域，用N(V)表示。

## 图的分类

按照边的特性，图可以被分类为无向图和有向图；按照边是否带权值，可以被分类为无权图和有权图；按照顶点之间是否有路径相连，可以被分类为连通图和非连通图。理解这些基础概念，对于后续进行图的操作和算法分析至关重要。

通过逐步深入以上内容，我们为接下来探讨图的存储方式及其算法性能影响打下了坚实的基础。

# 2. 图的存储方式及其对算法性能的影响

### 2.1 常见的图存储方法

图作为一种用来表达实体间关系的数据结构，其存储方式的选取对算法的性能有直接的影响。常见的图存储方法有两种：邻接矩阵和邻接表。不同的存储方法各有优势和适用场景，因此在具体应用中需要根据实际需求进行选择。

#### 2.1.1 邻接矩阵

邻接矩阵是一个二维数组，用于存储图中所有顶点之间的连接关系。对于无向图，其邻接矩阵是对称的；对于有向图，邻接矩阵则可能是非对称的。矩阵中的元素通常使用布尔值或整数来表示连接关系的存在与否或边的权重。

public class Graph {
    private final int[][] adjacencyMatrix;
    private final int verticesCount;

    public Graph(int verticesCount) {
        this.verticesCount = verticesCount;
        adjacencyMatrix = new int[verticesCount][verticesCount];
    }

    public void addEdge(int source, int destination, int weight) {
        adjacencyMatrix[source][destination] = weight;
        adjacencyMatrix[destination][source] = weight; // For undirected graph
    }
}

在上述代码中，`addEdge` 方法将两个顶点之间的边及其权重添加到邻接矩阵中。在无向图中，只要有一条边连接两个顶点，则矩阵的两个对称位置都需要更新。

#### 2.1.2 邻接表

邻接表是另一种图的存储方式，它使用链表或数组的数组来存储每条边的信息。每个顶点对应一个链表，链表中存储的是相邻顶点的列表。相较于邻接矩阵，邻接表在表示稀疏图时可以节省大量空间。

public class Graph {
    private final LinkedList<Integer>[] adjacencyList;
    private final int verticesCount;

    @SuppressWarnings("unchecked")
    public Graph(int verticesCount) {
        this.verticesCount = verticesCount;
        adjacencyList = new LinkedList[verticesCount];
        for (int i = 0; i < verticesCount; ++i)
            adjacencyList[i] = new LinkedList<>();
    }

    public void addEdge(int source, int destination, int weight) {
        adjacencyList[source].add(new Edge(destination, weight));
        if (source != destination) { // For undirected graph
            adjacencyList[destination].add(new Edge(source, weight));
        }
    }

    class Edge {
        int vertex;
        int weight;

        Edge(int vertex, int weight) {
            this.vertex = vertex;
            this.weight = weight;
        }
    }
}

上述代码定义了一个邻接表表示法，并提供了添加边的方法。`Edge` 类用来存储边的目标顶点和权重信息。

### 2.2 存储方式对图算法性能的影响

图的存储方式会直接影响图算法的性能，主要体现在时间和空间复杂度上。

#### 2.2.1 时间复杂度分析

使用邻接矩阵时，访问任意顶点的所有邻接顶点的时间复杂度是 O(V)，其中 V 是顶点的数量。对于稀疏图，这意味着有很多时间会被浪费在访问不存在的边（即访问数组中的零值）上。

使用邻接表时，时间复杂度取决于链表的平均长度，即邻接顶点的数量。在稀疏图中，邻接表通常可以提供更快的访问速度，因为链表中的元素数量较少。

#### 2.2.2 空间复杂度分析

邻接矩阵的空间复杂度是 O(V^2)，因为需要为每对顶点存储一个条目。即使是在完全不相连的图中，也需要存储 V^2 个空的条目。

邻接表的空间复杂度是 O(V + E)，其中 E 是边的数量。对于稀疏图，这种存储方式可以节省大量空间，因为它只需要存储实际存在的边。

### 2.3 案例分析：不同存储方法在实际应用中的选择

在实际应用中，根据图的大小和密集程度，选择合适的存储方法可以显著提升算法性能。

#### 2.3.1 小规模图的存储选择

对于小规模图，存储方法的选择可能对性能影响不大，但使用邻接表可以为将来可能的扩展留出空间。例如，在社交网络中，用户的好友关系通常以邻接表的形式存储，因为大多数用户的好友数量远小于总用户数，即图是稀疏的。

#### 2.3.2 大规模图的存储选择

对于大规模图，存储方式的选择对性能和资源消耗影响显著。例如，在大规模网络路由中，邻接矩阵可能导致极大的内存消耗，此时使用邻接表或压缩存储方法会更加高效。

### 总结

图的存储方式对图数据结构算法性能有显著影响。邻接矩阵在表示稠密图时表现良好，空间和时间复杂度高，而邻接表在稀疏图中更为有效率。在选择存储方式时，需考虑图的规模、稠密度以及算法需求，以实现最优的性能表现。在本章节中，我们通过理论分析和代码示例，对邻接矩阵和邻接表的实现和适用性进行了深入探讨。接下来的章节中，我们将深入Java中的图数据结构实现，探索更多高级操作和算法实现。

# 3. ```
# 第三章：Java中实现图数据结构的方法

在本章节中，我们将深入探讨Java语言中实现图数据结构的方法。这一部分的内容将会涉及图的基本构建元素，包括节点和边的类设计，以及图的表示方法。同时，本章节还将覆盖图算法框架的实现，包括图遍历框架和搜索算法的实现，最后探讨Java中图的高级操作实现，如最短路径算法的接口定义和辅助数据结构的设计。

## 使用Java构建图的基本类

### 图的节点类和边类的设计

构建图的基本单元是节点（Vertex）和边（Edge）。节点通常包含一个唯一的标识符以及可能与之相关联的任何其他信息。边表示节点之间的关系，通常包括一个起点、一个终点，以及可能的权重。

**代码块示例：**

public class Vertex {
    private String id;
    private String label;

    public Vertex(String id, String label) {
        this.id = id;
        this.label = label;
    }

    // Getters and setters
}

public class Edge {
    private Vertex source;
    private Vertex destination;
    private double weight;

    public Edge(Vertex source, Vertex destination, double weight) {
        this.source = source;
        this.destination = destination;
        this.weight = weight;
    }

    // Getters and setters
}

**参数说明：**
- `Vertex`: 节点类，包含节点的id和标签。
- `Edge`: 边类，包含起点、终点以及权重。

### 图的表示方法

图可以通过多种方式来表示。最常见的有两种：邻接矩阵和邻接表。每种表示方法都有其优势和不足，选择哪种方法取决于图的特性以及算法的需求。

**邻接矩阵**

在邻接矩阵表示中，图