Java双层循环最短路径算法：原理与实践

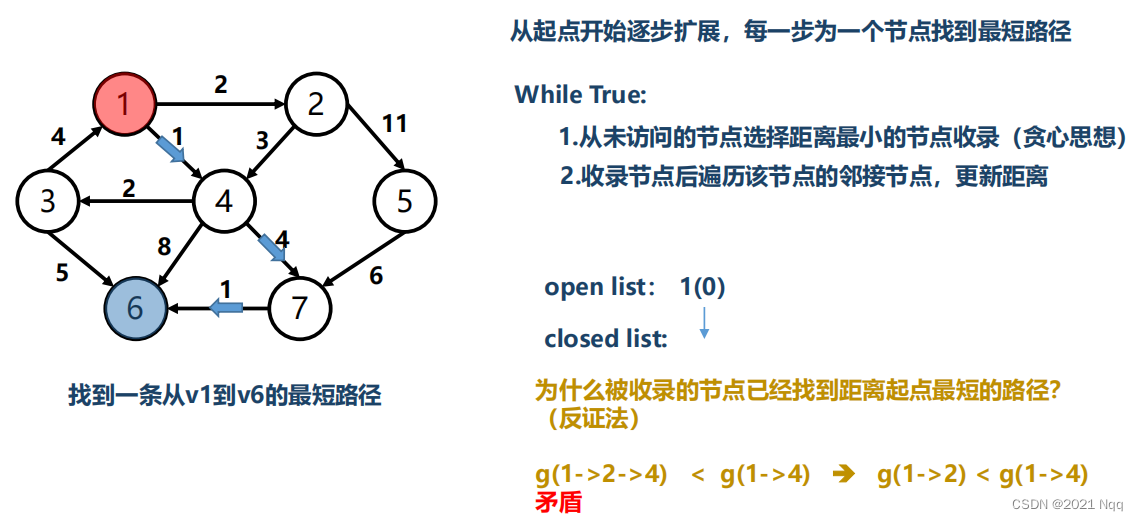
# 1. 双层循环算法概述

## 1.1 双层循环算法简介
双层循环算法是计算机科学中的一种基础算法，它通过嵌套循环的方式遍历数据结构中的元素，以实现特定的逻辑处理。这种算法在处理矩阵、图搜索和最短路径等问题时特别有效。

## 1.2 双层循环与最短路径问题
在最短路径问题中，双层循环算法通常用于实现经典算法，如Floyd-Warshall算法，该算法能够找到给定图中所有顶点对之间的最短路径。通过两层循环的组合，可以逐步构建出每对顶点间的最短路径。

## 1.3 算法的适用场景
双层循环算法适用于需要多重迭代处理的场景，例如在模拟、预测以及优化问题中。它的通用性和易理解性，使得它成为了算法教学和软件开发中不可或缺的一部分。

// 示例：使用双层循环计算两个数的最大公约数
public int gcd(int a, int b) {
    while(b != 0) {
        int temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}

本章概括了双层循环算法的基本概念和它在最短路径问题中的应用，为后续深入探讨最短路径算法提供了理论基础。

# 2. 最短路径算法的理论基础

## 2.1 图论与路径搜索

### 2.1.1 图的基本概念

在图论中，图是由顶点（也称为节点）和连接顶点的边组成的数据结构。图可以是有向的，也可以是无向的，这取决于边的方向性。在有向图中，边表示从一个顶点指向另一个顶点的单向连接；而在无向图中，边则表示顶点之间的双向连接。图可以用来模拟各种实际场景，如交通网络、社交网络、计算机网络等。

### 2.1.2 路径和距离的定义

路径是指在图中从一个顶点到另一个顶点经过的一系列边和顶点。路径的长度是路径上所有边的权重之和。最短路径问题就是在图中找到两个顶点之间路径长度最短的路径。路径的长度可以通过边的权重来衡量，如果图是无权重的，那么路径长度就是经过的边的数量。

### 2.1.3 有向图和无向图的差异

有向图和无向图的差异在于边的方向性，这影响了最短路径的搜索方式。在有向图中，我们需要考虑边的方向，而无向图则没有这个问题。有向图中可能存在某些顶点无法到达其他顶点的情况，而在无向图中，除非有孤立顶点，否则任意两个顶点都是相互可达的。

### 2.1.4 权重和距离的测量

在加权图中，边具有权重，表示通过这条边的“距离”或“成本”。最短路径算法的目标是在加权图中找到两个顶点之间的最小权重和路径。权重可以代表不同的意义，比如距离、时间、成本等。对于无权重图，路径的长度通常就是边的数量。

### 2.1.5 不同类型图的最短路径问题

不同类型图的最短路径问题存在差异。在加权图中，我们需要寻找权重和最小的路径；在无权重图中，我们需要寻找边的数量最少的路径。图还可以是有向无环图(DAG)，在这种图中，不存在从一个顶点到另一个顶点的环路，这简化了最短路径问题的解决。

## 2.2 最短路径问题的分类

### 2.2.1 单源最短路径问题

单源最短路径问题关注的是从一个特定的起点到所有其他顶点的最短路径。这可以使用Dijkstra算法或Bellman-Ford算法等经典算法解决。Dijkstra算法在没有负权边的图中效率较高，而Bellman-Ford算法则可以处理带有负权边的图。

### 2.2.2 所有顶点对最短路径问题

所有顶点对最短路径问题需要找出图中任意两点间的最短路径。这可以通过Floyd-Warshall算法实现，该算法通过动态规划的方式，逐步构建所有顶点对之间的最短路径。该算法的时间复杂度为O(n^3)，适用于顶点数较少的图。

### 2.2.3 特殊图的最短路径问题

在某些特殊类型的图中，最短路径问题可能有更加高效的解决方案。例如，在平面图中，可以使用欧几里得最短路径算法。在树状结构图中，问题可以转化为简单的递归或迭代搜索。

## 2.3 双层循环算法的原理

### 2.3.1 算法描述

双层循环算法是一种暴力解法，通过两层循环遍历所有可能的路径选择，计算出任意两点间的最短路径。对于每个顶点，算法检查通过其他所有顶点作为中转点的路径长度，以此来确定最短路径。

### 2.3.2 算法的时间复杂度分析

双层循环算法的时间复杂度为O(n^3)，其中n是顶点的数量。在最坏情况下，需要计算n*(n-1)/2条路径，并对每条路径执行长度计算，导致了高昂的计算成本。

### 2.3.3 双层循环算法的空间复杂度分析

空间复杂度方面，双层循环算法主要依赖于存储路径长度的二维数组，空间复杂度为O(n^2)。这意味着算法需要一个n×n的数组来存储每对顶点之间的最短路径长度。

双层循环算法虽然简单直观，但通常不是解决最短路径问题的最优方法。它的效率较低，尤其在顶点数量较多的图中，需要考虑更为高效的算法，比如Dijkstra算法、Bellman-Ford算法或者Floyd-Warshall算法。

### 双层循环算法的代码示例

以下是双层循环算法的伪代码，描述了其基本逻辑：

function all_pairs_shortest_paths(graph G):
    n = number of vertices in G
    distance = n x n matrix where distance[i][j] is the length of the shortest path from vertex i to vertex j
    for each vertex v in G:
        for i from 0 to n-1:
            for j from 0 to n-1:
                distance[i][j] = weight of edge (i, j)
                if i == j:
                    distance[i][j] = 0
                if edge (i, j) doesn't exist:
                    distance[i][j] = INFINITY
    for k from 0 to n-1:
        for i from 0 to n-1:
            for j from 0 to n-1:
                if distance[i][j] > distance[i][k] + distance[k][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]
    return distance

### 双层循环算法的性能优化

虽然双层循环算法的时间复杂度较高，但在特定场景下，我们可以通过以下优化策略来提升效率：

#### *.*.*.* 避免冗余计算

为了避免重复计算相同的路径，可以利用一个布尔数组来标记是否已经计算过某对顶点间的最短路径。

#### *.*.*.* 使用邻接矩阵优化空间

由于双层循环算法依赖于矩阵来存储路径长度，可以直接使用邻接矩阵来表示图。这样可以避免在每次迭代中计算顶点间的边的存在性。

双层循环算法在理论研究和教学中仍然具有其价值，但在实际应用中，更高效的算法通常是更佳的选择。通过理解这种基础方法，我们能够更好地欣赏并理解其他更高级的最短路径算法的优势。

# 3. Java实现双层循环算法

## 3.1 双层循环算法的数据结构设计
在本章节中，我们将深入探讨如何利用Java实现双层循环算法，首先需要对数据结构进行详细设计，以便为算法提供准确的图数据表示。

### 3.1.1 图的表示方法

图可以使用不同的数据结构表示，其中包括邻接矩阵和邻接表。在双层循环算法中，由于需要快速访问任意两个顶点之间的距离，邻接矩阵是更优的选择。邻接矩阵是一个二维数组，其中的元素表示图中两个顶点之间的权重。如果两个顶点之间没有直接的连接，则对应的权重设为一个非常大的数，通常使用整型的最大值表示。

### 3.1.2 权重和邻接矩阵的构建

int[][] adjacencyMatrix = new int[maxVertices][maxVertices];

// 初始化矩阵为无穷大
for (int i = 0; i < maxVertices; i++) {
    for (int j = 0; j < maxVertices; j++) {
        adjacencyMatrix[i][j] = Integer.MAX_VALUE;
    }
}