Java图论与最短路径入门：基础与实战攻略

# 1. 图论基础与Java实现概述

图论是数学的一个分支，它主要研究顶点（或节点）以及连接顶点的边的集合。图论提供了一种强大的抽象工具，用于建模各种现实世界的问题，比如社交网络、道路网络、电路等。在计算机科学领域，图论同样扮演着至关重要的角色，它在算法设计、网络分析、数据结构等领域都有广泛应用。

Java作为一种面向对象的编程语言，其数据类型和丰富的类库支持对图结构和算法的自然表示。使用Java实现图论算法不仅能深化对算法理论的理解，同时也能提高编程技能，特别是在对象管理和内存优化方面。

本章将对图论的基本概念进行介绍，并简要概述如何使用Java来实现图论相关的算法。从图的定义到如何在Java中表示图，再到具体实现图的基本操作，本章将为读者打下坚实的基础。这将为后文深入探讨不同类型的图遍历算法、最短路径算法以及图论在实际问题中的应用奠定基础。

# 2. 图的表示和数据结构

## 2.1 图论中的基本概念

### 2.1.1 图的定义和类型

在图论中，一个图（Graph）是由顶点（Vertices）的集合和顶点之间边（Edges）的集合组成的数据结构。边可以是有向的，也可以是无向的。有向边表示方向性，而无向边表示顶点之间的双向关系。

图可以分为几种类型：

- 无向图（Undirected Graph）：边不区分方向，比如社交网络中的朋友关系。
- 有向图（Directed Graph）：边有明确的方向，比如网页的超链接指向。
- 加权图（Weighted Graph）：边被赋予了一个权值，表示连接顶点的“代价”。
- 非加权图（Unweighted Graph）：边不带权值，通常表示顶点之间存在或不存在关系。

### 2.1.2 顶点、边、路径和环

顶点是图的基本构成单位，可以是抽象概念，如城市、人等。

边是顶点之间的连接线，可以是无向的（表示两者之间存在双向关系），也可以是有向的（表示方向性）。边可以是简单的（两个顶点间最多只有一条边）或多重的（两个顶点间可以有多条边）。

路径是一系列顶点通过一系列边相连的序列。路径的长度可以由经过的边的数量来衡量。

环（Cycle）是指一条路径的起始顶点和终止顶点是同一个顶点的特殊路径，且路径上的其他顶点都不重复出现。

## 2.2 图的Java表示方法

### 2.2.1 邻接矩阵

邻接矩阵是一种图的表示方法，它利用二维数组来表示图中的边。如果顶点i和顶点j之间存在一条边，则在邻接矩阵中的位置(i, j)和(j, i)上标记为1（或权值），否则为0。对于无向图，邻接矩阵是对称的。

int[][] adjacentMatrix = {
    {0, 1, 0, 0},
    {1, 0, 1, 1},
    {0, 1, 0, 1},
    {0, 1, 1, 0}
};

### 2.2.2 邻接表

邻接表使用链表或数组列表来表示顶点的相邻顶点列表，通常使用`HashMap`实现，其中键是顶点，值是与该顶点相邻的顶点列表。

import java.util.HashMap;
import java.util.Map;

Map<Integer, List<Integer>> adjacentList = new HashMap<>();
adjacentList.put(0, Arrays.asList(1));
adjacentList.put(1, Arrays.asList(0, 2, 3));
adjacentList.put(2, Arrays.asList(1, 3));
adjacentList.put(3, Arrays.asList(1, 2));

### 2.2.3 阵列列表和邻接映射

阵列列表是一个简化版的邻接表，适用于顶点编号连续且从0开始的情况。它用一个一维数组来存储所有顶点的邻接表。

邻接映射是邻接表的一种变体，它使用两个字典，一个字典记录顶点到其邻接顶点的映射，另一个字典记录顶点到其出边权值的映射。

下表展示了邻接矩阵和邻接表在表示同一个图时的差异：

| 图的表示方法 | 邻接矩阵 | 邻接表 |
|--------------|----------|--------|
| 描述 | 二维数组，边的存在用1或权值表示，不存在用0表示 | 用HashMap实现，顶点为键，与顶点相邻的顶点列表为值 |
| 空间复杂度 | O(V^2)，适用于顶点数较少的稠密图 | O(V + E)，适用于顶点数多边数少的稀疏图 |
| 优点 | 实现简单，检索两条特定顶点是否相邻的时间复杂度为O(1) | 空间利用率高，适合稀疏图的表示 |
| 缺点 | 空间利用率低，对稀疏图来说比较浪费 | 检索两条特定顶点是否相邻的时间复杂度为O(V) |

接下来，我们将讨论图的遍历算法，深入理解如何使用Java进行图的深度优先搜索（DFS）和广度优先搜索（BFS）遍历。

# 3. 图的遍历算法

在深入理解图论的基础知识和图的表示方法之后，接下来我们将探讨图的遍历算法。图的遍历算法是理解和分析图结构的重要手段，它允许我们访问图中每一个顶点，以便进行进一步的处理或分析。在此章节中，我们将重点学习两种基本的图遍历算法：深度优先搜索（DFS）和广度优先搜索（BFS），以及它们在解决实际问题中的应用。

## 3.1 深度优先搜索（DFS）

### 3.1.1 DFS的原理和实现

深度优先搜索是一种用于图的遍历或搜索树的算法。它尽可能深地搜索图的分支，直到路径的末端，然后回溯并探索下一条路径。

为了实现深度优先搜索，通常使用递归或栈数据结构。以下是DFS的实现流程：

1. 从图中的某个顶点v开始。
2. 标记顶点v为已访问。
3. 对于v的每一个未访问的邻接顶点w，递归调用DFS函数。

下面是使用Java实现DFS的一个简单示例：

import java.util.*;

public class Graph {
    private int V;   // 图的顶点数
    private LinkedList<Integer> adj[]; // 邻接表

    // DFS的递归实现
    public void DFSUtil(int v, boolean visited[]) {
        // 当前节点标记为已访问
        visited[v] = true;
        System.out.print(v + " ");

        // 访问所有未访问的邻接顶点
        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    public Graph(int v) {
        this.V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    // 添加边
    public void addEdge(int v, int w) {
        adj[v].add(w);
    }

    // DFS遍历
    public void DFS(int v) {
        // 默认所有顶点未访问
        boolean visited[] = new boolean[V];

        // 调用递归辅助函数，遍历所有顶点
        DFSUtil(v, visited);
    }

    public static void main(String args[]) {
        Graph g = new Graph(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println("深度优先遍历（从顶点2开始）:");
        g.DFS(2);
    }
}

上述代码创建了一个包含四个顶点的图，并且定义了边的连接。之后，我们从顶点2开始进行深度优先搜索，并打印出访问顶点的顺序。

### 3.1.2 应用DFS解决实际问题

DFS算法不仅在图的遍历中发挥作用，而且在解决实际问题时也有广泛应用。例如，它常用于解决诸如迷宫求解、拓扑排序、查找连通分量、检测环以及网络爬虫中网页的深度优先遍历等问题。

在迷宫求解中，DFS可以用来寻找一条从起点到终点的路径，通过不断尝试不同的路径分支直到找到出口。在计算机网络中，DFS可以用于拓扑排序，根据节点的依赖关系对项目进行排序。

此外，DFS还能用来检测图中是否存在环。在有向图中，如果在DFS过程中访问的节点被再次访问，则说明存在环。这个特性可以用于例如对依赖关系进行循环依赖检查。

## 3.2 广度优先搜索（BFS）

### 3.2.1 BFS的原理和实现

广度优先搜索是一种遍历或搜索树或图的算法。它从根节点开始，逐层向外扩展，直到所有节点都被访问。

BFS通常使用队列数据结构来实现。下面是BFS实现的步骤：

1. 创建一个队列，并将根节点入队。
2. 当队列不为空时，进行以下步骤：
a. 队头元素出队，并将其标记为已访问。
b. 将队头元素的所有未访问的邻接节点入队。

以下是使用Java实现BFS的一个示例代码：

import java.util.*;

public class Graph {
    private int V;   // 图的顶点数
    private LinkedList<Integer> adj[]; // 邻接表

    // BFS遍历从给定顶点v开始
    public void BFS(int v) {
        // 标记所有顶点为未访问
        boolean visited[] = new boolean[V];
        // 创建一个队列用于BFS
        LinkedList<Integer> queue = new LinkedList<Integer>();

        // 标记当前节点为已访问并入队
        visited[v] = true;
        queue.add(v);

        while (queue.size() != 0) {
            // 出队一个顶点并打印
            v = queue.poll();
            System.out.print(v + " ");

            // 获取所有邻接顶点
            Iterator<Integer> i = adj[v].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n]) {
                    visited[n] = true;
                    queue.add(n);
                }
            }
        }
    }

    // ... Graph类的其他方法与DFS相同，此处略过 ...
    public static void main(String args[]) {
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println("广度优先遍历（从顶点2开始）:");
        g.BFS(2);
    }
}

### 3.2.2 应用BFS解决实际问题

BFS在实际问题中的应用也十分广泛。例如，在社交网络分析中，可以使用BFS算法来找出用户之间的最短关系链路，帮助分析信息的传播路径。在游戏设计中，BFS常用于路径查找，以寻找最短路径到达目标点。

在计算机网络领域中，BFS可用于网络故障检测，遍历所有节点以确定哪些节点无法访问。在最短路径问题中，BFS用于未加权图中寻找两个顶点之间的最短路径，因为最先访问到的目标节点必然是最短路径上的节点。

BFS的层级遍历特性还使得它在层次化的数据结构分析中非常有用，比如在决策树和层次化聚类中。此外，BFS由于其特点，也常被用于各种优化算法中，比如用于优化搜索空间以避免不必要的计算。

通过本章节的介绍，我们了解了深度优先搜索（DFS）和广度优先搜索（BFS）的原理和具体实现，以及它们在解决实际问题中的应用。深度优先搜索适用于深入探索图结构，而广度优先搜索则适用于快速找到从起始点出发的最短路径。在下一章节中，我们将继续探索图论中最为重要的算法之一：最短路径算法。

# 4. 最短路径算法理论与实现

## 4.1 最短路径问题概述

### 4.1.1 问题定义与应用场景

最短路径问题是图论中一个著名的经典问题，它涉及在加权图中找到两个顶点之间的最小权重路径。对于某些应用场景来说，这个概念可能是一个城市间的最短路线，或者是在网络中传输数据包的最快路由。在这些情境中，效率和成本是主要的考虑因素。

在定义最短路径问题时，我们通常会考虑以下几点：

- **有向图**与**无向图**：有向图的边是有方向的，必须按照特定方向前进；无向图则可以双向通行。
- **带权图**与**非带权图**：带权图中的边有相对应的权重或成本。
- **单源最短路径问题**：给定图中的一个顶点作为源点，找到该点到图中所有其他点的最短路径。
- **多源最短路径问题**：找到图中所有顶点对之间的最短路径。

最短路径算法广泛应用于多个领域，例如：

- **城市导航系统**，计算从一个地点到另一个地点的最短道路。
- **网络通信**，确定数据包通过网络从一个节点到另一个节点的最快路径。
- **社交网络分析**，比如寻找网络中两个用户之间传播信息的最短路径。
- **生物信息学**，分析蛋白质网络的路径。

### 4.1.2 算法性能比较

在选择最短路径算法时，需要考虑几个关键的性能指标，包括时间复杂度、空间复杂度以及特定场景的适用性。比较流行的算法包括Dijkstra算法和Bellman-Ford算法，它们各自在不同场景下有所优势和限制。

- **Dijkstra算法**：适用于没有负权重边的图。它的时间复杂度为O(V^2)或O(E + VlogV)，其中V是顶点数，E是边数。该算法的空间复杂度为O(V)。
- **Bellman-Ford算法**：能够处理带有负权重边的图，且可以在图中存在负权重循环的情况下进行检测。它的时间复杂度为O(VE)，空间复杂度同样为O(V)。

通常，如果确定图中没有负权重边，则Dijkstra算法将是一个更优的选择，因为它的运行速度快。但如果图中存在负权重边，Bellman-Ford算法将是必须使用的。

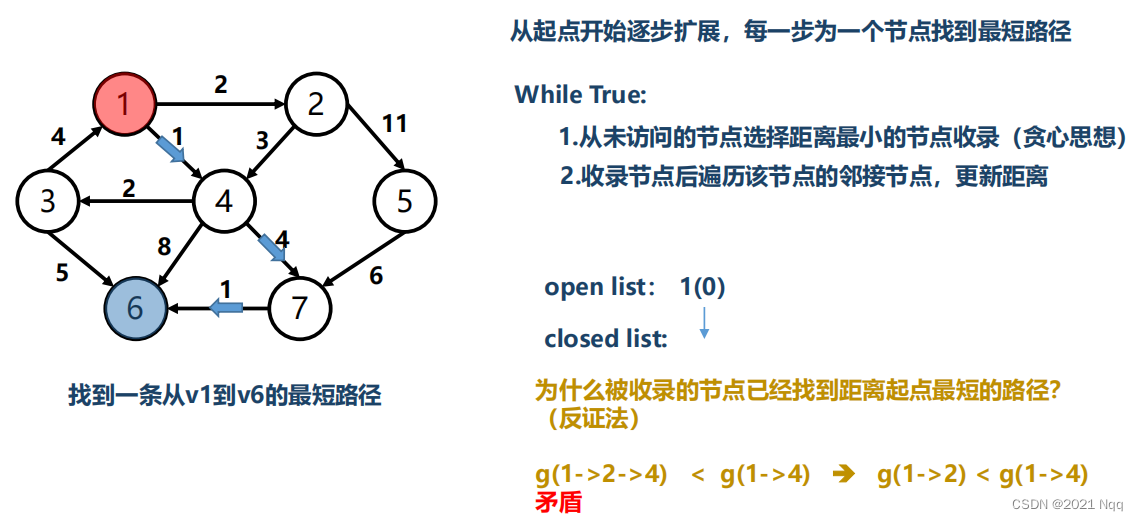
## 4.2 Dijkstra算法原理与Java实现

### 4.2.1 算法原理

Dijkstra算法利用贪心策略，从源点开始逐步将最近的未访问顶点作为下一个访问点，并更新与这些顶点相邻的顶点到源点的最短距离。算法结束时，我们得到从源点到图中所有其他顶点的最短路径。

算法步骤如下：

1. 初始化所有顶点到源点的距离为无穷大，除了源点自己为零。
2. 创建一个未访问顶点集合。
3. 选择距离源点最近的一个未访问顶点。
4. 更新与该顶点相邻的未访问顶点的最短路径值。
5. 将该顶点标记为已访问，并从未访问集合中移除。
6. 如果所有顶点都被访问，或者未访问顶点集合为空，则算法结束。
7. 重复步骤3到6，直到找到目标顶点的最短路径或所有顶点都被访问。

### 4.2.2 代码实现与优化

下面是一个Dijkstra算法的Java实现示例：

import java.util.Arrays;

public class DijkstraAlgorithm {

    // A utility function to find the vertex with minimum distance value, from
    // the set of vertices not yet included in shortest path tree
    private static int minDistance(int[] dist, boolean[] sptSet, int V) {
        int min = Integer.MAX_VALUE, minIndex = -1;

        for (int v = 0; v < V; v++)
            if (sptSet[v] == false && dist[v] <= min)
                min = dist[v], minIndex = v;

        return minIndex;
    }

    // Function that implements Dijkstra's single source shortest path algorithm
    // for a graph represented using adjacency matrix representation
    public void dijkstra(int[][] graph, int src) {
        int V = graph.length;
        int[] dist = new int[V]; // The output array. dist[i] will hold the shortest
                                 // distance from src to i

        boolean[] spt