【Java面试必备：数据结构在回文判断中的应用】：巧解面试题

# 1. 数据结构与回文判断的概念

## 理解数据结构基础
在计算机科学中，数据结构是存储、组织数据的方式，它旨在提高数据的处理效率。数据结构可以分为基本数据结构和复杂数据结构。基本数据结构包括数组、链表、栈、队列等，而复杂数据结构则涉及树、图、哈希表、字典树等。

## 回文判断的定义
回文是一个正读和反读都相同的字符串或数字序列。在数据结构中，回文判断是一个常见的问题，它的目的是为了确定一个序列是否为回文。无论是字符串、数字、链表还是数组，都可能需要进行回文判断。

## 数据结构与回文判断的联系
不同的数据结构提供了不同的方式来实现回文判断。例如，数组和字符串通过索引访问元素，而链表、栈、队列则需要遍历元素。理解这些基本的数据结构，对于设计高效的回文判断算法至关重要。接下来的章节将具体探讨如何利用不同的数据结构来实现回文判断，以及相关算法的设计与优化。

# 2. 基本数据结构在回文判断中的应用

## 2.1 字符串和数组基础

### 2.1.1 字符串与数组的特性

字符串是由字符组成的数组，它是一个线性表数据结构，用于存储一系列字符。字符串和数组都是由元素组成，这些元素在内存中是连续存放的。数组可以包含任意类型的数据，而字符串是数组的一个特例，只能包含字符数据。

字符串和数组的基本操作包括遍历、查找、插入、删除、排序等。在回文判断中，这些操作被用来分析字符串的对称性。数组或字符串的元素可以通过索引来访问和修改，这为回文判断提供了一种便利的方式。

### 2.1.2 字符串与数组的常用操作

字符串与数组的常用操作，如：

- `length()` 或 `sizeof()`：获取数组或字符串的长度。
- `at(index)` 或 `charAt(index)`：根据索引访问元素。
- `append(value)` 或 `push(value)`：在数组末尾添加元素。
- `insert(index, value)`：在指定位置插入元素。
- `deleteAt(index)` 或 `pop()`：删除指定位置的元素。

在回文判断中，最核心的操作是检查字符串或数组是否从前往后读和从后往前读是一致的。

### 代码块与逻辑分析

def is_palindrome(s):
    return s == s[::-1]  # Python切片操作，s[::-1]将返回一个反转后的字符串

这个Python函数`is_palindrome`接收一个字符串`s`，并返回一个布尔值，指示该字符串是否是回文。代码中`[::-1]`利用了Python切片操作的特性，它能够高效地将字符串反转，并比较原字符串与反转后的字符串是否相同。

### 2.2 链表结构的回文判断

#### 2.2.1 链表的概念及应用场景

链表是一种线性数据结构，由一系列节点组成。每个节点包含数据和指向下一个节点的指针。链表不像数组那样需要连续的内存空间，这使得链表在插入和删除操作中更加高效。

链表在实际编程中常用于实现栈、队列、哈希表以及其它复杂的数据结构。链表的灵活性使其成为处理动态数据的理想选择。

#### 2.2.2 链表实现回文判断的算法思路

判断链表是否为回文需要考虑空间复杂度的限制。一种有效的算法思路是先将链表内容复制到数组中，然后使用双指针方法来比较数组两端的元素。如果在遍历过程中两端的元素始终相等，则链表是回文。

#### 2.2.3 链表回文判断的代码实现

struct Node {
    int data;
    struct Node *next;
};

bool isPalindrome(struct Node* head) {
    if (head == NULL || head->next == NULL)
        return true;

    // Step 1: Reverse the second half of the list
    struct Node *slow = head, *fast = head, *prev = NULL;
    while (fast && fast->next) {
        prev = slow;
        slow = slow->next;
        fast = fast->next->next;
    }
    prev->next = NULL;  // Cut the list at the middle

    // Step 2: Reverse the second half of the list
    struct Node *firstHalf = head;
    struct Node *secondHalf = reverseList(slow);

    // Step 3: Check if the first and second halfs are identical
    while (secondHalf) {
        if (firstHalf->data != secondHalf->data)
            return false;
        firstHalf = firstHalf->next;
        secondHalf = secondHalf->next;
    }
    return true;
}

### 2.3 栈和队列结构的回文判断

#### 2.3.1 栈与队列的基本原理

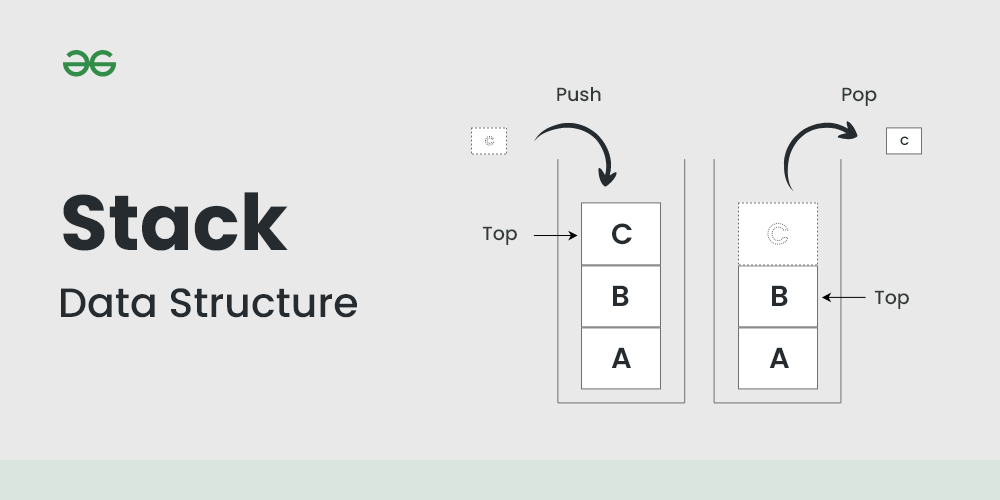
栈是一种后进先出（LIFO）的数据结构，只能在一端进行插入和删除操作。栈的操作主要有两个：`push`（添加元素到栈顶）和`pop`（移除栈顶元素）。队列则是一种先进先出（FIFO）的数据结构，允许在两端进行操作，分别是`enqueue`（添加元素到队尾）和`dequeue`（从队首移除元素）。

#### 2.3.2 利用栈进行回文判断

回文判断可以通过将字符串的一半字符依次推入栈中，然后依次弹出栈顶元素与另一半的字符进行比较。如果所有字符都匹配，则说明该字符串是回文。

#### 2.3.3 利用队列进行回文判断

与栈不同，队列要求两部分字符串同时处理。可以将一半的字符添加到队列中，然后用队列进行两次出队操作，并与另一半进行比较。需要注意的是，队列不具备栈那样的后进先出特性，因此这个方法需要额外的逻辑来处理字符串的后半部分。

## 表格展示

在进行回文判断时，我们可能会使用到以下数据结构及其特点，下面是一个对比表格：

| 数据结构 | 特点 | 优点 | 缺点 | 回文判断适用场景 |
| --- | --- | --- | --- | --- |
| 数组/字符串 | 连续内存空间，可通过索引直接访问 | 访问速度快 | 不易动态调整大小 | 简单直接的回文判断 |
| 链表 | 不需要连续内存空间，灵活的动态调整 | 插入删除效率高 | 难以随机访问 | 需要频繁增删的回文判断 |
| 栈 | 后进先出 | 实现简单，适用场景多 | 只能从一端操作 | 用于回文判断的辅助结构 |
| 队列 | 先进先出 | 遵循实际排队逻辑 | 无法反向操作 | 与栈结合使用进行回文判断 |

以上表格简单展示了在回文判断中常用的数据结构及其适用场景，强调了它们在不同情况下的优缺点，帮助读者根据具体情况选择合适的数据结构。

# 3. 复杂数据结构与高级回文判断策略

在探讨了基本数据结构在回文判断中的应用后，我们将进一步深入复杂数据结构与高级回文判断策略的研究。复杂数据结构如树、哈希表和字典树(Trie)等，为回文判断提供了更为灵活和高效的手段。本章将介绍这些结构在回文判断中的应用，解析其背后的原理和实际应用中的技巧。

## 3.1 树结构与回文判断

### 3.1.1 二叉树基础及其遍历方法

二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。理解二叉树的构建和遍历方法是掌握二叉树在回文判断中应用的基础。

在二叉树的遍历中，我们主要关注三种基本方式：前序遍历、中序遍历和后序遍历。前序遍历是先访问根节点，再递归地进行前序遍历左子树，然后递归地进行前序遍历右子树。中序遍历和后序遍历的原理类似，区别在于访问根节点的时机。

# 以下为一个简单的二叉树节点类和前序遍历方法的实现示例
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def preorder_traversal(root):
    if not root:
        return []
    return [root.val] + preorder_traversal(root.left) + preorder_traversal(root.right)

在上述代码中，我们首先定义了一个二叉树节点类`TreeNode`，然后实现了前序遍历的方法`preorder_traversal`。此方法递归地访问根节点并分别递归遍历左子树和右子树。

### 3.1.2 利用二叉树结构进行回文判断

利用二叉树进行回文判断，通常是将字符串或者数组转换为某种特定的树结构，如二叉搜索树（BST）或者平衡二叉树（如AVL树或红黑树）。然后利用树的特性来判断字符串或序列是否为回文。

例如，在BST中，如果左右子树都满足回文特性且根节点值等于中心点，则该BST满足回文。需要注意的是，并非所有的二叉树结构都适合用来进行回文判断，通常需要根据具体的回文定义选择合适的树结构。

### 3.1.3 利用二叉树进行回文判断的代码实现

下面给出一个利用二叉树实现回文判断的代码示例：

# 以下是一个利用二叉树进行回文判断的示例代码
cl