【回归问题中的AdaBoost】：理论与实现的完美结合

# 1. 回归问题中的AdaBoost基本概念

AdaBoost（Adaptive Boosting）是机器学习领域中一个非常重要的集成学习算法，尤其擅长处理分类问题。但在本章节中，我们将聚焦于AdaBoost在回归问题中的应用。回归问题是指预测一个连续值输出，如温度、股价等，与分类问题不同的是，回归问题的输出不是离散的标签。

## 1.1 AdaBoost在回归问题中的作用

在回归问题中，AdaBoost通过迭代的方式构建一系列的回归模型，通常以决策树为基学习器，然后将它们组合起来，形成一个强回归器。每一轮迭代都会对前一轮的错误进行“适应性”强化，给予那些难于预测的数据更大的权重。

## 1.2 AdaBoost与传统回归方法的区别

不同于传统的回归分析方法（如线性回归或岭回归），AdaBoost不是寻求全局最优的参数解，而是通过弱回归器的叠加来改善预测性能，特别是当问题难以用单一模型解决时，这种方法特别有效。

本章的目的是让读者对AdaBoost在回归问题中的角色和功能有一个初步的认识，为深入探索其理论基础和实现细节打下基础。

# 2. AdaBoost算法的理论基础

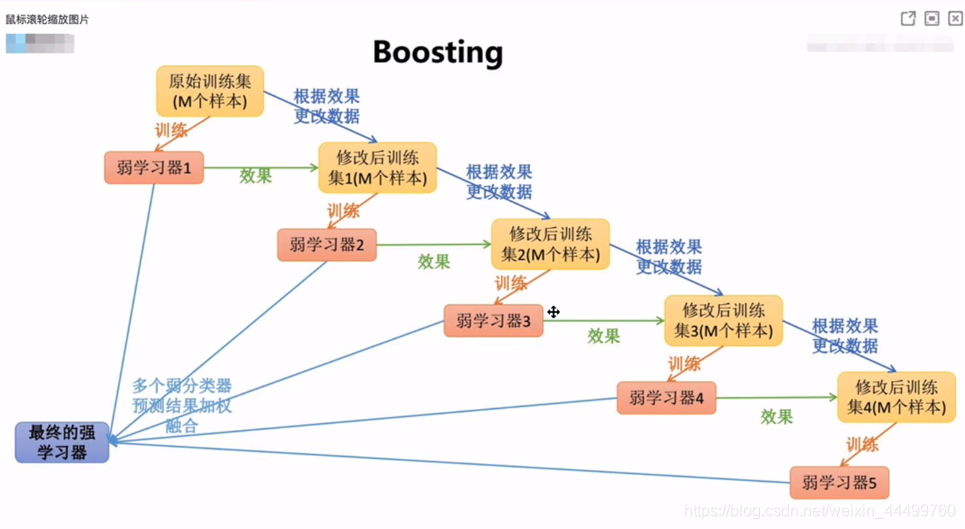
## 2.1 Boosting方法概述

### 2.1.1 Boosting原理简介

Boosting是一种集成学习方法，它通过构建并结合多个分类器来解决单一模型可能存在的偏差和方差问题。与随机森林等并行集成方法不同，Boosting采用的是串行集成，每一个新的分类器都是在上一个分类器的错误基础上进行训练，以此来弥补前者的不足。AdaBoost是Boosting算法中最著名的一个成员，它通过调整样本权重来重点训练那些被前一个模型错误分类的样例。

### 2.1.2 Boosting方法的类型与发展

Boosting的发展历程中，一些重要的算法包括AdaBoost、梯度提升树（Gradient Boosting Trees）和XGBoost等。AdaBoost是最原始的Boosting算法，它通过改变样本权重的方式实现，而梯度提升树通过优化损失函数的梯度来实现模型的提升。XGBoost在梯度提升树的基础上进一步优化了算法性能，引入了正则项和高效的并行计算，成为当前机器学习竞赛中常用的模型之一。

## 2.2 AdaBoost算法原理

### 2.2.1 AdaBoost的工作机制

AdaBoost的工作机制是通过迭代地训练一系列的弱学习器，每次迭代都会根据弱学习器的表现来调整训练数据集的权重。在每一轮迭代中，被错误分类的样本权重增加，而被正确分类的样本权重减少。随后，基于更新后的权重分布，选择一个新的弱学习器进行训练。这个过程重复进行，直到达到预设的迭代次数或者弱学习器的性能不再有显著提升。

### 2.2.2 损失函数与权重更新

在AdaBoost中，损失函数通常用指数损失函数来衡量模型的预测误差，其形式为：
\[ L(y,f(x)) = e^{-y \cdot f(x)} \]
其中，\(y\) 表示真实标签，\(f(x)\) 表示预测值。权重更新的策略是指数函数的负梯度方向，即给定样本权重 \(w_i\) 的更新规则为：
\[ w_i^{(t)} = w_i^{(t-1)} \cdot e^{\alpha_t \cdot y_i \cdot f_t(x_i)} \]
其中，\( \alpha_t \) 表示在第 \(t\) 轮迭代中弱学习器的权重，\(f_t(x_i)\) 表示第 \(t\) 轮弱学习器的预测值，而 \(y_i\) 是样本的真实标签。

## 2.3 AdaBoost的优化与扩展

### 2.3.1 AdaBoost的变种

AdaBoost的变种包括但不限于SAMME（stagewise additive modeling using a multi-class exponential loss function）和SAMME.R。SAMME是针对多分类问题的AdaBoost改进版，而SAMME.R则是其改进中的随机版本，采用随机子空间方法来进一步提升模型的泛化能力。这些变种尝试通过不同的策略来改进原始AdaBoost在某些问题上的不足。

### 2.3.2 算法性能的理论界限

理论分析显示，当弱学习器的表现略好于随机猜测时（即误差率小于50%），AdaBoost模型可以被提升到任意高的性能上限。然而，当弱学习器的表现退化到随机猜测水平时，AdaBoost算法可能会出现过拟合现象。因此，在实践中，选择一个表现良好的弱学习器是非常重要的。

接下来，我们将深入探讨AdaBoost算法的实现细节，以及如何通过代码实现这一强大的算法，并讨论在实现过程中遇到的关键问题和解决方案。

# 3. AdaBoost算法的实现细节

#### 3.1 算法流程与代码框架

##### 3.1.1 AdaBoost的伪代码分析

AdaBoost算法的核心思想是通过组合多个弱学习器来构建一个强学习器。以下是算法的伪代码实现，它描述了如何利用迭代的方式逐步构建出一个强大的分类器。

初始化权重分布D1(i)=1/N, i=1,2,...,N
对于m=1,2,...,M：
    1. 使用Dm训练弱学习器h_m(x)
    2. 计算h_m(x)的错误率ε_m
    3. 计算α_m=1/2*ln((1-ε_m)/ε_m)，即模型权重
    4. 更新权重分布Dm+1(i)=Dm(i)*exp(-α_m*y_i*h_m(x_i))/Z_m
    Z_m是规范化因子，确保Dm+1为一个分布
返回最终的强学习器F(x)=sign(Σα_m*h_m(x))

在伪代码中，`α_m` 是学习器的权重，反映了该学习器在整体分类器中的重要性。权重的更新是基于模型的错误率，错误率越低，权重越大。权重分布`D_m`的更新则通过指数函数，给予正确分类的样本较低的权重，错误分类的样本较高的权重，从而使得下一个学习器能够关注上一个学习器误分类的样本。

##### 3.1.2 算法参数设置与调试

在实际应用中，我们需要注意以下几个关键参数的设置与调试：

- **迭代次数M**：决定了最终模型的复杂度。过小会导致模型欠拟合，过大可能引起过拟合。
- **弱学习器类型**：可以是决策树、感知机等。不同的弱学习器影响最终模型的性能。
- **学习率α**：控制弱学习器对最终模型的贡献度。较小的学习率有利于模型稳定，但需要更多的迭代次数。
- **权重更新方式**：通常使用指数函数，但也可以尝试其他形式的更新。

通常，需要通过交叉验证和网格搜索等方法对这些参数进行优化，找到一个适应于具体数据集的最优解。

#### 3.2 弱学习器的选择与集成

##### 3.2.1 决策树作为弱学习器

在AdaBoost中，决策树是最常用的弱学习器之一。这是因为决策树易于理解，且在小规模数据集上能够迅速捕捉到数据的关键特征。单个决策树被称为决策桩（Decision Stump）。

单层决策树的实现通常非常简单：

from sklearn.tree import DecisionTreeClassifier

# 创建决策桩
dtree = DecisionTreeClassifier(max_depth=1)

对于决策树作为弱学习器的实现，我们需要迭代地训练每个树，并根据权重更新来关注那些之前模型预测错误的样本。

##### 3.2.2 其他弱学习器的集成策略

除了决策树，AdaBoost也可以集成其他类型的弱学习器，例如线性回归、支持向量机、神经网络等。集成策略需要根据弱学习器的特性和问题类型进行合理选择。

在集成神经网络的情况下，每一轮迭代中训练的神经网络可以被看作是弱学习器，其输出经过加权后形成最终的强学习器。

from keras.models import Sequential
from keras.layers import Dense

# 创建单层神经网络
model = Sequential()
model.add(Dense(10, input_dim=input_shape, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

神经网络的权重更新将遵循AdaBoost的权重更新规则，通过适当的损失函数确保弱学习器能够专注于前一轮模型预测错误的样本。

#### 3.3 实现中的关键问题与解决方案

##### 3.3.1 过拟合问题与避免方法

过拟合是指模型在训练数据上表现良好，但是在未见过的数据上表现较差的现象。在AdaBoost中，因为模型依赖于多个弱学习器，所以有较高的过拟合风险。

为避免过拟合，我们可以采取以下策略：

- 限制迭代次数M，避免模型过度复杂。
- 采用更为简单的弱学习器，比如较浅的决策树。
- 引入正则化项或惩罚项，对模型进行约束。