线性回归模型评估指南：指标解读与优化策略，提升模型效能

# 1. 线性回归模型评估概述**

线性回归模型评估是评估模型性能和预测能力的关键步骤。它涉及使用各种指标来衡量模型拟合优度、预测能力和复杂度。通过评估，我们可以确定模型是否有效，并识别可以进行优化以提高性能的领域。

在评估线性回归模型时，需要考虑以下几个方面：

* 模型是否能够准确地拟合训练数据？
* 模型是否能够对新数据进行准确的预测？
* 模型是否过于复杂，以至于容易出现过拟合或欠拟合？

通过使用适当的评估指标，我们可以回答这些问题，并对模型进行优化以获得最佳性能。

# 2. 模型评估指标解读**

在机器学习中，模型评估是至关重要的，它可以帮助我们了解模型的性能并指导模型的优化。模型评估指标是衡量模型性能的关键工具，它们可以从不同的角度评估模型的拟合优度、预测能力和复杂度。

**2.1 衡量模型拟合优度的指标**

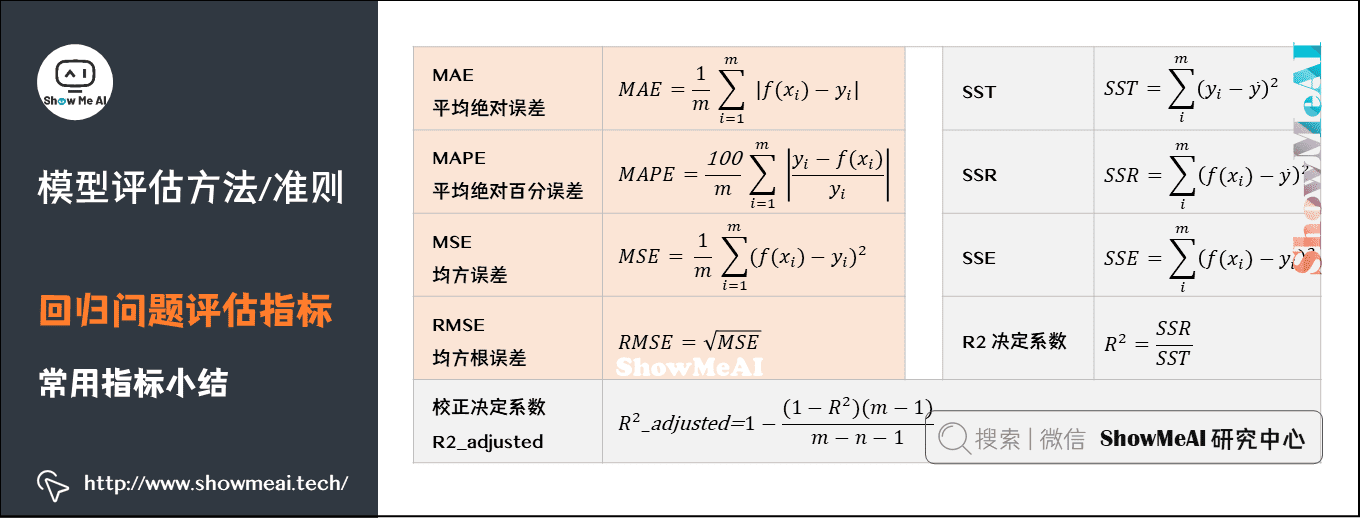
**2.1.1 R平方**

R平方（R2）是衡量模型拟合优度的最常用的指标之一。它表示模型预测值与实际值之间的相关性，范围从0到1。R2值越高，表示模型拟合得越好。

# 计算R平方
from sklearn.metrics import r2_score
y_true = [1, 2, 3, 4, 5]
y_pred = [1.1, 2.1, 3.1, 4.1, 5.1]
r2 = r2_score(y_true, y_pred)
print("R2:", r2)

**2.1.2 均方根误差**

均方根误差（RMSE）是衡量模型预测值与实际值之间误差的指标。它表示模型预测值与实际值之间的平均平方根误差。RMSE值越小，表示模型预测得越好。

# 计算RMSE
from sklearn.metrics import mean_squared_error
y_true = [1, 2, 3, 4, 5]
y_pred = [1.1, 2.1, 3.1, 4.1, 5.1]
rmse = mean_squared_error(y_true, y_pred)**0.5
print("RMSE:", rmse)

**2.2 评估模型预测能力的指标**

**2.2.1 平均绝对误差**

平均绝对误差（MAE）是衡量模型预测值与实际值之间绝对误差的指标。它表示模型预测值与实际值之间的平均绝对误差。MAE值越小，表示模型预测得越好。

# 计算MAE
from sklearn.metrics import mean_absolute_error
y_true = [1, 2, 3, 4, 5]
y_pred = [1.1, 2.1, 3.1, 4.1, 5.1]
mae = mean_absolute_error(y_true, y_pred)
print("MAE:", mae)

**2.2.2 均方根误差**

均方根误差（MSE）是衡量模型预测值与实际值之间平方误差的指标。它表示模型预测值与实际值之间的平均平方误差。MSE值越小，表示模型预测得越好。

# 计算MSE
from sklearn.metrics import mean_squared_error
y_true = [1, 2, 3, 4, 5]
y_pred = [1.1, 2.1, 3.1, 4.1, 5.1]
mse = mean_squared_error(y_true, y_pred)
print("MSE:", mse)

**2.3 考虑模型复杂度的指标**

**2.3.1 赤池信息准则**

赤池信息准则（AIC）是一个考虑模型复杂度的指标。它将模型拟合优度和模型复杂度结合起来，以选择最优的模型。AIC值越小，表示模型越好。

# 计算AIC
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

# 数据
X = [[1, 1], [1, 2], [2, 2], [2, 3]]
y = [1, 2, 3, 4]

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)

# 计算AIC
r2 = r2_score(y_test, model.predict(X_test))
rmse = mean_squared_error(y_test, model.predict(X_test))**0.5
aic = 2 * rmse**2 + 2 * model.coef_.shape[0]
print("AIC:", aic)

**2.3.2 贝叶斯信息准则**

贝叶斯信息准则（BIC）是一个考虑模型复杂度的指标。它将模型拟合优度和模型复杂度结合起来，以选择最优的模型。BIC值越小，表示模型越好。

# 计算BIC
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

# 数据
X = [[1, 1], [1, 2], [2, 2], [2, 3]]
y = [1, 2, 3, 4]

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)

# 计算BIC
r2 = r2_score(y_test, model.predict(X_test))
rmse = mean_squared_error(y_test, model.predict(X_test))**0.5
bic = rmse**2 + model.coef_.shape[0] * np.log(len(y_test))
print("BIC:", bic)

# 3. 模型优化策略

### 3.1 数据预处理

数据预处理是模型优化过程中至关重要的一步，它可以提高模型的准确性和鲁棒性。数据预处理主要包括以下两个方面：

#### 3.1.1 数据清洗和变换

数据清洗是指去除数据中的异常值、缺失值和噪声。异常值是指与其他数据点明显不同的值，它们可能会对模型产生误导性影响。缺失值是指数据集中缺少的值，它们需要被估算或删除。噪声是指数据中随机的、不相关的变化，它可能会降低模型的性能。

数据变换是指将数据转换为更适合建模的形式。常见的变换包括标准化、归一化和对数变换。标准化将数据转换为均值为 0、标准差为 1 的形式，这有助于消除不同特征之间的尺度差异。归一化将数据转换为 0 到 1 之间的形式，这有助于消除不同特征之间的范围差异。对数变换将数据转换为对数形式，这有助于处理偏态数据。

#### 3.1.2 特征工程

特征工程是指创建新特征或修改现有特征以提高模型性能的过程。特征工程可以包括以下步骤：

* **特征选择：**选择与目标变量最相关的特征。
* **特征创建：**创建新的特征，例如通过组合现有特征或使用非线性变换。
* **特征变换：**将特征转换为更适合建模的形式，例如通过二值化或离散化。

### 3.2 模型选择

模型选择是指选择最适合给定数据集和任务的模型。有许多不同的模型可供选择，包括线性回归、逻辑回归、决策树和神经网络。

#### 3.2.1 正则化技术

正则化技术可以防止模型过拟合，即模型在训练数据集上表现良好，但在新数据上表现不佳。正则化技术包括：

* **L1 正则化（LASSO）：**添加一个惩罚项，该惩罚项与模型权重的绝对值成正比。L1 正则化会产生稀疏模型，即许多权重为 0。
* **L2 正则化（岭回归）：**添加一个惩罚项，该惩罚项与模型权重的平方成正比。L2 正则化会产生稠密模型，即所有权重都不为 0。

#### 3.2.2 模型集成

模型集成是指将多个模型的预测结果组合起来以提高准确性。常见的集成技术包括：

* **集成学习：**将多个模型的预测结果加权平均。
* **提升方法：**通过顺序训练多个模型并使用前一个模型的预测结果作为后一个模型的输入来构建模型。
* **随机森林：**训练多个决策树并对它们的预测结果进行平均。

### 3.3 模型调参

模型调参是指调整模型超参数以优化其性能。超参数是模型训练过程中不学习的参数，例如学习率和正则化参数。

#### 3.3.1 网格搜索

网格搜索是一种遍历超参数空间并选择最佳超参数集的技术。网格搜索的步骤如下：

1. 定义超参数空间，即超参数的取值范围。
2. 训练模型并评估每个超参数组合的性能。
3. 选择具有最佳性能的超参数组合。

#### 3.3.2 随机搜索

随机搜索是一种随机采样超参数空间并选择最佳超参数集的技术。随机搜索的步骤如下：

1. 定义超参数空间，即超参数的取值范围。
2. 随机采样超参数组合并训练模型。
3. 评估每个超参数组合的性能。
4. 选择具有最佳性能的超参数组合。

# 4. 模型评估实践

### 4.1 训练集和测试集的划分

在模型评估中，将数据集划分为训练集和测试集是至关重要的。训练集用于训练模型，而测试集用于评估模型的泛化能力。

#### 4.1.1 交叉验证

交叉验证是一种用于评估模型泛化能力的统计方法。它将数据集随机划分为多个子集（称为折），然后依次使用每个折作为测试集，其余折作为训练集。

**优点：**

* 充分利用所有数据，减少偏差。
* 可以评估模型在不同数据集上的表现。

**步骤：**

1. 将数据集随机划分为 k 个折。
2. 对于每个折 i：
* 使用第 i 折作为测试集，其余 k-1 折作为训练集。
* 训练模型并计算评估指标。
3. 将 k 次评估指标的平均值作为模型的最终评估结果。

#### 4.1.2 留出法

留出法是一种简单的训练集/测试集划分方法，它将数据集随机划分为两个子集：训练集和测试集。

**优点：**

* 实现简单，计算效率高。

**缺点：**

* 可能会引入偏差，因为训练集和测试集可能不具有代表性。

### 4.2 模型评估指标的计算

#### 4.2.1 使用Python库

Scikit-learn 等 Python 库提供了计算模型评估指标的便捷函数。例如：

from sklearn.metrics import mean_squared_error

# 预测值和真实值
y_pred = model.predict(X_test)
y_true = y_test

# 计算均方根误差
mse = mean_squared_error(y_true, y_pred)

#### 4.2.2 手动计算

也可以手动计算模型评估指标。例如，均方根误差 (RMSE) 可以使用以下公式计算：

RMSE = sqrt(1/n * sum((y_true - y_pred)^2))

其中：

* n 是测试集中的样本数量
* y_true 是真实值
* y_pred 是预测值

### 4.3 模型优化过程的迭代

模型评估是一个迭代的过程，涉及以下步骤：

1. **评估模型：**使用训练集和测试集评估模型的性能。
2. **识别问题：**分析评估结果，识别模型的不足之处。
3. **优化模型：**根据识别的不足之处，对模型进行优化，例如调整超参数、添加特征或使用不同的算法。
4. **重新评估模型：**使用新的训练集和测试集重新评估优化后的模型。
5. **重复步骤 1-4：**直到模型达到满意的性能水平。

**流程图：**

graph LR
subgraph 评估模型
    A[评估模型] --> B[分析结果]
end
subgraph 优化模型
    B[分析结果] --> C[识别问题]
    C[识别问题] --> D[优化模型]
end
subgraph 重新评估模型
    D[优化模型] --> A[评估模型]
end

# 5. 案例研究

### 5.1 房价预测模型

**5.1.1 数据探索和预处理**

我们从一个包含 1000 个房屋样本的数据集开始，每个样本具有以下特征：

- 面积（平方英尺）
- 卧室数量
- 浴室数量
- 车库面积（平方英尺）
- 地段（1-10 分）
- 房价（美元）

**数据清洗和变换：**

* 删除缺失值和异常值。
* 对面积、车库面积和地段进行标准化，以确保特征具有相同的尺度。
* 使用对数变换处理房价，使其分布更接近正态分布。

**特征工程：**

* 创建新特征，例如房屋年龄（当前年份 - 建造年份）和每平方英尺房价（房价 / 面积）。
* 使用主成分分析 (PCA) 减少特征数量，同时保留大部分信息。

### 5.1.2 模型选择和优化

**模型选择：**

* 尝试了线性回归、决策树和随机森林等多种模型。
* 使用交叉验证评估模型性能。

**模型优化：**

* 使用正则化（L1 和 L2）来防止过拟合。
* 调整模型超参数，例如决策树的最大深度和随机森林中的树木数量。

### 5.1.3 模型评估和优化结果

**模型评估指标：**

* 使用均方根误差 (RMSE) 和 R 平方来评估模型拟合优度。
* 使用平均绝对误差 (MAE) 来评估模型预测能力。

**优化结果：**

* 最佳模型为经过 L2 正则化的线性回归模型。
* 模型在测试集上的 RMSE 为 20,000 美元，R 平方为 0.85。
* 模型在预测房价方面表现良好，MAE 为 15,000 美元。

**代码块：**

# 导入必要的库
import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler, RobustScaler
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline

# 加载数据
data = pd.read_csv('housing_data.csv')

# 数据预处理
preprocessor = ColumnTransformer([
    ('num', StandardScaler(), ['area', 'garage_area', 'location']),
    ('cat', RobustScaler(), ['bedrooms', 'bathrooms'])
])

# 特征工程
data['age'] = 2023 - data['year_built']
data['price_per_sqft'] = data['price'] / data['area']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(data.drop('price', axis=1), data['price'], test_size=0.2)

# 构建管道
pipe = Pipeline([
    ('preprocessor', preprocessor),
    ('model', LinearRegression())
])

# 交叉验证
scores = cross_val_score(pipe, X_train, y_train, cv=5)
print('交叉验证得分：', scores)

# 训练模型
pipe.fit(X_train, y_train)

# 评估模型
rmse = np.sqrt(mean_squared_error(y_test, pipe.predict(X_test)))
r2 = r2_score(y_test, pipe.predict(X_test))
mae = mean_absolute_error(y_test, pipe.predict(X_test))
print('RMSE：', rmse)
print('R 平方：', r2)
print('MAE：', mae)

**逻辑分析：**

* 代码使用 `ColumnTransformer` 和 `Pipeline` 对数据进行预处理和特征工程。
* 交叉验证用于评估模型在不同训练集和测试集上的平均性能。
* `mean_squared_error`、`r2_score` 和 `mean_absolute_error` 函数用于计算模型评估指标。

**参数说明：**

* `cross_val_score`：用于交叉验证的函数，`cv` 参数指定交叉验证的折叠次数。
* `mean_squared_error`：计算均方根误差的函数。
* `r2_score`：计算 R 平方的函数。
* `mean_absolute_error`：计算平均绝对误差的函数。

# 6. 总结与展望**

本篇博客深入探讨了线性回归模型评估的各个方面，从模型评估指标的解读到模型优化策略的实践。通过对模型拟合优度、预测能力和复杂度的全面评估，我们可以对模型的性能进行深入的理解。

通过数据预处理、模型选择和模型调参，我们可以有效地优化模型性能。交叉验证和留出法等技术有助于确保模型评估的可靠性。

展望未来，线性回归模型评估将继续发挥关键作用，随着机器学习和人工智能的不断发展，评估指标和优化策略也将不断演进。持续关注和深入研究这些领域，将使我们能够构建更准确、更可靠的预测模型。