线性回归算法全攻略：从原理到应用，让你预测无忧

# 1. 线性回归算法概述**

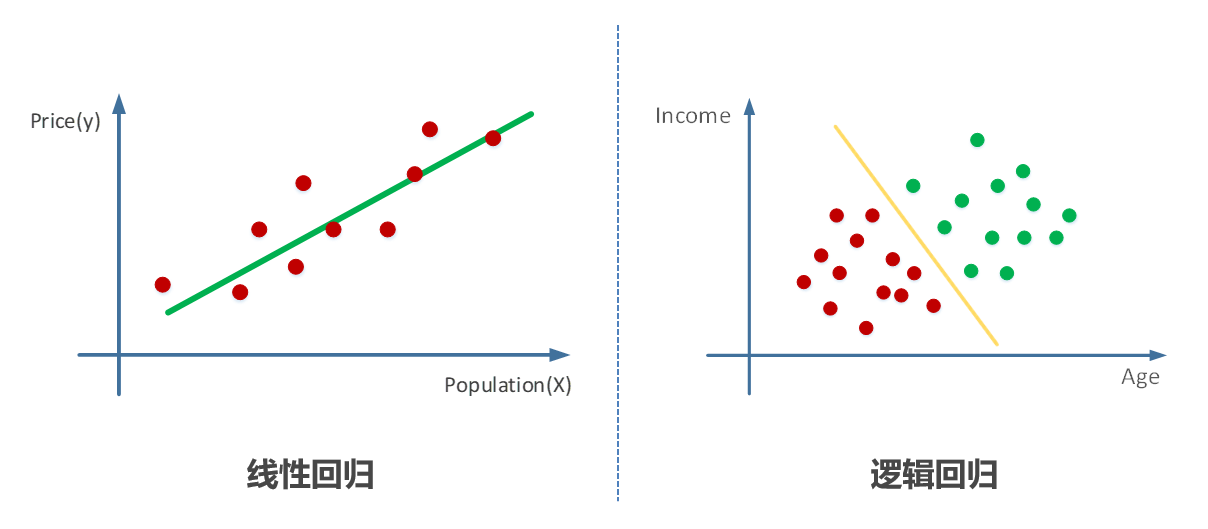
线性回归是一种监督机器学习算法，用于预测连续型目标变量。它假设目标变量与自变量之间存在线性关系。线性回归算法旨在找到一条最佳拟合直线，使得预测值与真实值之间的误差最小。

线性回归算法的优点包括：

- **易于理解和实现：**线性回归算法的原理简单明了，易于理解和实现。
- **计算效率高：**线性回归算法的计算复杂度较低，训练和预测速度快。
- **鲁棒性好：**线性回归算法对异常值和噪声数据具有较好的鲁棒性。

# 2. 线性回归算法原理

### 2.1 线性模型与最小二乘法

线性回归算法是一种监督学习算法，用于预测连续值的目标变量。其基本假设是目标变量与自变量之间存在线性关系，即：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y：目标变量
* x1, x2, ..., xn：自变量
* β0, β1, ..., βn：线性回归模型的系数
* ε：误差项，表示观测值与模型预测值之间的差异

最小二乘法是线性回归算法中常用的优化方法，其目标是找到一组系数 β0, β1, ..., βn，使误差项 ε 的平方和最小。通过求解以下方程组，可以得到最优系数：

(X'X)β = X'y

其中：

* X：自变量的矩阵
* X'：X 的转置矩阵
* y：目标变量的向量

### 2.2 线性回归方程的推导

线性回归方程的推导基于最小二乘法原理。假设我们有 n 个观测值，每个观测值包含 m 个自变量和一个目标变量。我们可以将观测值表示为以下矩阵形式：

X = [x11 x12 ... x1m
     x21 x22 ... x2m
     ...  ...  ...  ...
     xn1 xn2 ... xnm]

y = [y1
     y2
     ...
     yn]

其中：

* X 是一个 n x m 的矩阵，包含自变量的值
* y 是一个 n x 1 的向量，包含目标变量的值

线性回归方程可以表示为：

y = Xβ + ε

其中：

* β 是一个 m x 1 的向量，包含线性回归模型的系数
* ε 是一个 n x 1 的向量，包含误差项

最小二乘法的目标是找到 β，使 ε'ε 最小。通过求解以下方程组，可以得到最优系数 β：

(X'X)β = X'y

求解该方程组，可以得到：

β = (X'X)^-1X'y

其中：

* (X'X)^-1 是 X'X 的逆矩阵

### 2.3 正则化和过拟合

正则化是一种技术，用于防止线性回归模型过拟合。过拟合是指模型在训练数据集上表现良好，但在新数据上表现不佳的情况。正则化通过向损失函数添加一个惩罚项来实现，该惩罚项与模型系数的大小成正比。

常用的正则化方法有：

* L1 正则化：惩罚模型系数的绝对值
* L2 正则化：惩罚模型系数的平方

正则化参数 λ 控制惩罚的强度。λ 越大，对模型系数的惩罚越大，模型越不容易过拟合。

# 3. 线性回归算法实践

### 3.1 数据准备与探索性分析

在开始构建线性回归模型之前，数据准备和探索性分析至关重要。这些步骤有助于了解数据的特征，识别异常值，并为模型选择提供信息。

**数据准备**

* **收集数据：**从相关来源收集与预测目标相关的变量数据。
* **数据清洗：**处理缺失值、异常值和错误数据，以确保数据的完整性和可靠性。
* **特征工程：**根据业务知识和统计技术，创建新特征或转换现有特征，以提高模型性能。

**探索性分析**

* **可视化数据：**使用散点图、直方图和箱线图等可视化技术探索变量之间的关系，识别异常值和数据分布。
* **计算统计量：**计算变量的均值、中位数、标准差和相关系数，以了解数据的中心趋势、离散程度和相关性。
* **识别异常值：**使用统计技术（如 Grubbs 检验）或可视化方法（如箱线图）识别异常值，并考虑将其删除或转换。

### 3.2 模型训练与评估

**模型训练**

* **选择模型：**根据数据的特征和预测目标选择合适的线性回归模型，例如普通最小二乘法 (OLS) 或岭回归。
* **训练模型：**使用训练数据集训练模型，优化模型参数以最小化损失函数（如均方误差）。
* **超参数调优：**调整模型的超参数（如正则化参数），以提高模型性能。

**模型评估**

* **训练集评估：**使用训练数据集评估模型的性能，以避免过拟合。
* **验证集评估：**使用验证数据集评估模型的泛化能力，即在未见数据上的表现。
* **评估指标：**使用均方根误差 (RMSE)、平均绝对误差 (MAE) 和 R² 等指标评估模型的性能。

### 3.3 模型部署与应用

**模型部署**

* **选择部署平台：**选择合适的平台（如云服务或本地服务器）来部署模型。
* **集成模型：**将模型集成到应用程序或系统中，以提供预测功能。
* **监控模型：**定期监控模型的性能，并根据需要进行重新训练或调整。

**模型应用**

* **预测：**使用模型对新数据进行预测，并根据预测结果做出决策。
* **决策支持：**将模型结果纳入决策过程中，以提高决策的准确性和效率。
* **优化：**使用模型来优化业务流程，例如库存管理或客户细分。

# 4. 线性回归算法进阶

### 4.1 多元线性回归

**定义**

多元线性回归是一种扩展的线性回归算法，它允许使用多个自变量来预测一个因变量。与简单的线性回归不同，多元线性回归模型的方程形式为：

y = b0 + b1x1 + b2x2 + ... + bnxn

其中：

* y 是因变量
* x1、x2、...、xn 是自变量
* b0、b1、...、bn 是模型系数

**优点**

多元线性回归的主要优点包括：

* **提高预测精度：**使用多个自变量可以捕获更复杂的关系，从而提高预测精度。
* **识别重要变量：**通过分析模型系数，可以确定对因变量影响最大的自变量。
* **解释力更强：**多元线性回归模型可以提供对预测结果的更深入解释。

**缺点**

多元线性回归也有一些缺点：

* **过拟合风险：**随着自变量数量的增加，过拟合的风险也会增加。
* **解释性较差：**当自变量数量较多时，模型方程可能难以解释。
* **计算复杂度：**多元线性回归模型的计算比简单线性回归模型更复杂。

### 4.2 非线性回归

**定义**

非线性回归是一种线性回归算法的扩展，它允许因变量和自变量之间存在非线性关系。非线性回归模型的方程形式可以是任意形式，例如：

y = a * exp(b * x)
y = a + b * log(x)
y = a * x^2 + b * x + c

**优点**

非线性回归的主要优点包括：

* **处理非线性关系：**非线性回归模型可以捕获因变量和自变量之间复杂的非线性关系。
* **提高预测精度：**对于非线性数据，非线性回归模型可以提供比线性回归模型更高的预测精度。

**缺点**

非线性回归也有一些缺点：

* **计算复杂度：**非线性回归模型的计算比线性回归模型更复杂。
* **过拟合风险：**非线性回归模型更容易过拟合，需要仔细选择模型复杂度。
* **解释性较差：**非线性回归模型的方程形式可能难以解释。

### 4.3 模型选择与交叉验证

**模型选择**

模型选择是选择最优模型的过程，以在预测精度和模型复杂度之间取得平衡。模型选择方法包括：

* **赤池信息准则 (AIC)：**AIC 是一种衡量模型复杂度和拟合优度的指标。AIC 值越低，模型越好。
* **贝叶斯信息准则 (BIC)：**BIC 是一种类似于 AIC 的指标，但它对模型复杂度的惩罚更大。
* **交叉验证：**交叉验证是一种评估模型泛化能力的方法。它将数据集分成多个子集，并使用其中一个子集进行训练，而使用其他子集进行验证。

**交叉验证**

交叉验证是一种评估模型泛化能力的方法。它涉及以下步骤：

1. 将数据集分成 k 个子集。
2. 对于每个子集 i：
* 使用其他 k-1 个子集训练模型。
* 使用子集 i 验证模型。
3. 计算模型在所有 k 个子集上的平均验证误差。

交叉验证可以帮助防止过拟合，并提供模型泛化能力的更可靠估计。

# 5. 线性回归算法在实际应用中的案例

### 5.1 房价预测

**场景描述：**

房价预测是线性回归算法最常见的应用之一。通过收集房子的特征信息（如面积、卧室数量、地理位置等），我们可以建立一个线性回归模型来预测房子的价格。

**数据准备：**

房价预测需要收集大量房子的历史销售数据，包括面积、卧室数量、地理位置等特征信息。这些数据可以从房地产网站或政府机构获取。

**模型训练：**

收集数据后，我们可以使用线性回归算法训练模型。训练过程包括：

1. **数据预处理：**对数据进行归一化或标准化，以消除特征之间的量纲差异。
2. **特征选择：**选择与房价相关性较高的特征，以提高模型的预测准确性。
3. **模型拟合：**使用最小二乘法或其他优化算法拟合线性回归方程。

**模型评估：**

模型训练完成后，我们需要评估模型的性能。常用的评估指标包括：

* **均方误差 (MSE)：**衡量预测值与实际值之间的平均平方差。
* **均方根误差 (RMSE)：**MSE 的平方根，表示预测误差的平均幅度。
* **决定系数 (R2)：**衡量模型解释数据变异程度的指标，取值范围为 0 到 1，1 表示模型完美拟合。

**模型部署：**

评估完成后，我们可以将模型部署到生产环境中，用于预测新房子的价格。

### 5.2 股票价格预测

**场景描述：**

股票价格预测是另一个常见的线性回归应用。通过收集股票的历史价格数据和影响价格的因素（如经济指标、公司业绩等），我们可以建立一个线性回归模型来预测股票的未来价格。

**数据准备：**

股票价格预测需要收集大量股票的历史价格数据，以及影响价格的因素数据。这些数据可以从金融数据网站或公司财报中获取。

**模型训练：**

与房价预测类似，股票价格预测也需要经过数据预处理、特征选择和模型拟合的过程。

**模型评估：**

股票价格预测的评估指标与房价预测类似，包括 MSE、RMSE 和 R2。此外，还可以使用其他指标，如：

* **夏普比率：**衡量模型预测收益与风险的比率。
* **最大回撤：**衡量模型预测收益的最大损失幅度。

**模型部署：**

评估完成后，我们可以将模型部署到生产环境中，用于预测股票的未来价格，辅助投资决策。

### 5.3 销售额预测

**场景描述：**

销售额预测是线性回归算法在商业领域的应用。通过收集销售历史数据和影响销售的因素（如广告支出、市场趋势等），我们可以建立一个线性回归模型来预测未来的销售额。

**数据准备：**

销售额预测需要收集大量销售历史数据，以及影响销售的因素数据。这些数据可以从公司内部数据库或外部市场研究机构获取。

**模型训练：**

销售额预测的模型训练过程与房价预测和股票价格预测类似。

**模型评估：**

销售额预测的评估指标包括 MSE、RMSE 和 R2。此外，还可以使用其他指标，如：

* **平均绝对百分比误差 (MAPE)：**衡量预测值与实际值之间的平均绝对误差百分比。
* **平均预测误差 (MPE)：**衡量预测值与实际值之间的平均误差。

**模型部署：**

评估完成后，我们可以将模型部署到生产环境中，用于预测未来的销售额，辅助业务决策。

# 6. 线性回归算法的局限性和未来发展

线性回归算法虽然是一种强大的预测工具，但它也存在一些局限性，需要我们注意：

### 局限性

- **线性假设：**线性回归假设数据之间的关系是线性的，但现实世界中许多数据并不满足线性关系。
- **过拟合：**当模型过于复杂时，可能会出现过拟合现象，即模型在训练集上表现良好，但在新数据上表现不佳。
- **外推：**线性回归模型只能在输入特征空间内进行预测，超出该范围的预测可能不准确。
- **鲁棒性差：**线性回归对异常值和噪声数据敏感，这些数据可能会影响模型的性能。

### 未来发展

为了克服这些局限性，研究人员正在探索以下方向：

- **非线性回归：**开发更灵活的模型来处理非线性关系，例如决策树、神经网络等。
- **正则化技术：**改进正则化方法以减少过拟合，例如 L1 正则化、L2 正则化等。
- **模型选择：**研究更有效的模型选择方法，例如交叉验证、贝叶斯信息准则 (BIC) 等。
- **鲁棒回归：**开发对异常值和噪声数据更鲁棒的回归算法，例如 M 型估计、L1 正则化回归等。

随着机器学习领域的不断发展，线性回归算法也将不断演进，以解决更复杂的问题，提供更准确的预测。