CDF实战指南：从概率计算到随机变量建模

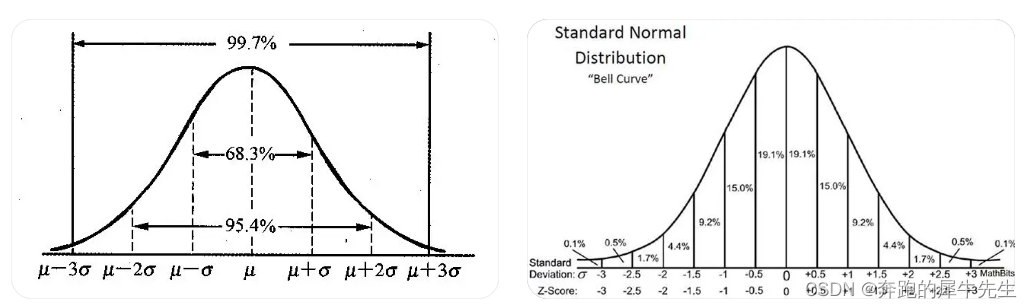
# 1. 概率论基础

概率论是随机变量建模的基础。它提供了计算事件发生可能性的数学框架。

### 1.1 事件与概率

事件是样本空间中一个子集。概率是事件发生的可能性，取值范围为 [0, 1]。概率为 0 表示事件不可能发生，概率为 1 表示事件必然发生。

### 1.2 概率公理

概率论建立在以下公理之上：

- **非负性：**每个事件的概率都大于或等于 0。
- **规范性：**样本空间的概率为 1。
- **可加性：**两个互斥事件的概率等于这两个事件概率之和。

# 2. 随机变量建模

随机变量是概率论中的基本概念，它描述了具有随机性的现象。随机变量建模是将随机现象用数学模型表示的过程，以便对其进行分析和预测。

### 2.1 离散型随机变量

#### 2.1.1 概率质量函数

离散型随机变量是指取值范围为有限或可数无限集合的随机变量。其概率分布由概率质量函数（PMF）描述，表示为：

P(X = x) = f(x)

其中：

* `X` 是随机变量
* `x` 是随机变量的取值
* `f(x)` 是概率质量函数

概率质量函数满足以下性质：

* `f(x) ≥ 0`，对于所有 `x`
* `Σf(x) = 1`，对于所有 `x`

#### 2.1.2 期望值和方差

离散型随机变量的期望值和方差定义如下：

* **期望值（均值）：**

E(X) = Σx * f(x)

* **方差：**

Var(X) = Σ(x - E(X))^2 * f(x)

期望值表示随机变量的平均值，方差表示随机变量分布的离散程度。

### 2.2 连续型随机变量

#### 2.2.1 概率密度函数

连续型随机变量是指取值范围为连续集合的随机变量。其概率分布由概率密度函数（PDF）描述，表示为：

f(x)

其中：

* `X` 是随机变量
* `x` 是随机变量的取值
* `f(x)` 是概率密度函数

概率密度函数满足以下性质：

* `f(x) ≥ 0`，对于所有 `x`
* `∫f(x)dx = 1`，对于所有 `x`

#### 2.2.2 期望值和方差

连续型随机变量的期望值和方差定义如下：

* **期望值（均值）：**

E(X) = ∫x * f(x)dx

* **方差：**

Var(X) = ∫(x - E(X))^2 * f(x)dx

期望值和方差的含义与离散型随机变量相同。

**代码示例：**

# 离散型随机变量
import numpy as np

# 概率质量函数
pmf = np.array([0.2, 0.3, 0.4, 0.1])

# 取值
x = np.array([1, 2, 3, 4])

# 期望值
mean = np.sum(x * pmf)
print("期望值：", mean)

# 方差
variance = np.sum((x - mean)**2 * pmf)
print("方差：", variance)

# 连续型随机变量
from scipy.stats import norm

# 概率密度函数
pdf = norm.pdf

# 期望值
mean = norm.mean()
print("期望值：", mean)

# 方差
variance = norm.var()
print("方差：", variance)

**Mermaid 流程图：**

graph LR
subgraph 离散型随机变量
    A[概率质量函数] --> B[期望值]
    A[概率质量函数] --> C[方差]
end
subgraph 连续型随机变量
    D[概率密度函数] --> E[期望值]
    D[概率密度函数] --> F[方差]
end

# 3. CDF的计算

CDF（累积分布函数）是概率论中一个重要的概念，它描述了随机变量在某个特定值以下或等于该值的概率。在本章节中，我们将讨论如何计算离散型和连续型随机变量的CDF。

### 3.1 离散型随机变量的CDF

对于离散型随机变量，其CDF可以通过以下公式计算：

F(x) = P(X ≤ x) = ∑_{k=0}^x p(x_k)

其中：

- `F(x)` 是随机变量 `X` 在 `x` 处的CDF
- `p(x_k)` 是随机变量 `X` 取值为 `x_k` 的概率

例如，考虑一个掷骰子的实验，其中随机变量 `X` 表示骰子掷出的点数。该随机变量的概率质量函数为：

p(x) = 1/6, x = 1, 2, 3, 4, 5, 6

则该随机变量的CDF为：

F(x) = P(X ≤ x) = ∑_{k=0}^x p(x_k) = 
{
    0, x < 1
    1/6, x = 1
    2/6, x = 2
    3/6, x = 3
    4/6, x = 4
    5/6, x = 5
    1, x ≥ 6
}

### 3.2 连续型随机变量的CDF

对于连续型随机变量，其CDF可以通过以下公式计算：

F(x) = P(X ≤ x) = ∫_{-∞}^x f(t) dt

其中：

- `F(x)` 是随机变量 `X` 在 `x` 处的CDF
- `f(x)` 是随机变量 `X` 的概率密度函数

例如，考虑一个正态分布的随机变量 `X`，其概率密度函数为：

f(x) = (1/√(2πσ^2)) * e^(-(x-μ)^2/(2σ^2))

其中：

- `μ` 是正态分布的均值
- `σ` 是正态分布的标准差

则该随机变量的CDF为：

F(x) = P(X ≤ x) = ∫_{-∞}^x f(t) dt = (1/2) * (1 + erf((x-μ)/(√(2)σ)))

其中：

- `erf(x)` 是误差函数

通过计算CDF，我们可以确定随机变量在某个特定值以下或等于该值的概率。这对于概率计算、随机变量的分布分析和统计推断等应用非常重要。

# 4. CDF的应用**

**4.1 概率计算**

CDF的主要应用之一是概率计算。给定一个随机变量X的CDF F(x)，我们可以计算X落在特定区间内的概率。例如，要计算X落在区间[a, b]内的概率，我们可以使用以下公式：

P(a ≤ X ≤ b) = F(b) - F(a)

**代码块：**

import numpy as np

# 离散型随机变量的概率计算
def discrete_probability(x, pmf):
    """
    计算离散型随机变量X在x处取值的概率。

    参数：
        x: 随机变量X的取值
        pmf: 概率质量函数

    返回：
        X在x处取值的概率
    """
    if x not in pmf:
        return 0
    else:
        return pmf[x]

# 连续型随机变量的概率计算
def continuous_probability(x, pdf):
    """
    计算连续型随机变量X在x处取值的概率密度。

    参数：
        x: 随机变量X的取值
        pdf: 概率密度函数

    返回：
        X在x处取值的概率密度
    """
    return pdf(x)

**逻辑分析：**

* `discrete_probability`函数用于计算离散型随机变量的概率。它检查给定的值是否在概率质量函数中，如果是，则返回该值对应的概率，否则返回0。
* `continuous_probability`函数用于计算连续型随机变量的概率密度。它直接返回给定值对应的概率密度。

**4.2 随机变量的分布**

CDF还可以用来描述随机变量的分布。分布函数的形状和特性可以提供有关随机变量行为的重要信息。例如，正态分布的CDF呈钟形，表示随机变量的值通常集中在平均值附近。

**4.3 统计推断**

CDF在统计推断中也发挥着重要作用。我们可以使用CDF来计算置信区间和假设检验的p值。例如，我们可以使用CDF来计算给定样本均值落在特定区间内的概率，从而判断样本均值是否与总体均值有显着差异。

**代码块：**

import scipy.stats as stats

# 计算置信区间
def confidence_interval(sample_mean, sample_std, sample_size, alpha=0.05):
    """
    计算给定样本均值、样本标准差和样本大小的置信区间。

    参数：
        sample_mean: 样本均值
        sample_std: 样本标准差
        sample_size: 样本大小
        alpha: 置信水平（默认值为0.05）

    返回：
        置信区间
    """
    z_score = stats.norm.ppf(1 - alpha / 2)
    margin_of_error = z_score * sample_std / np.sqrt(sample_size)
    lower_bound = sample_mean - margin_of_error
    upper_bound = sample_mean + margin_of_error
    return lower_bound, upper_bound

# 计算假设检验的p值
def hypothesis_test(sample_mean, population_mean, sample_std, sample_size, alternative="two-sided"):
    """
    计算给定样本均值、总体均值、样本标准差和样本大小的假设检验的p值。

    参数：
        sample_mean: 样本均值
        population_mean: 总体均值
        sample_std: 样本标准差
        sample_size: 样本大小
        alternative: 备择假设（"two-sided"、"less"或"greater"）

    返回：
        假设检验的p值
    """
    t_score = (sample_mean - population_mean) / (sample_std / np.sqrt(sample_size))
    if alternative == "two-sided":
        p_value = 2 * stats.t.cdf(-abs(t_score), sample_size - 1)
    elif alternative == "less":
        p_value = stats.t.cdf(t_score, sample_size - 1)
    elif alternative == "greater":
        p_value = 1 - stats.t.cdf(t_score, sample_size - 1)
    return p_value

**逻辑分析：**

* `confidence_interval`函数用于计算置信区间。它使用正态分布的百分位数来计算置信区间的上下限。
* `hypothesis_test`函数用于计算假设检验的p值。它使用学生t分布来计算p值，并根据备择假设选择不同的计算方法。

# 5. CDF的建模**

CDF的建模是指根据给定的数据或知识，建立一个能够描述随机变量分布的概率分布函数。CDF的建模方法主要有以下三种：

**5.1 经验分布函数**

经验分布函数（EDF）是根据给定的数据样本估计出的概率分布函数。EDF的计算公式如下：

F(x) = (1/n) * ∑_{i=1}^{n} I(X_i <= x)

其中：

* F(x) 是经验分布函数
* n 是样本容量
* X_i 是样本中的第 i 个数据点
* I(X_i <= x) 是指示函数，当 X_i <= x 时为 1，否则为 0

EDF 的优点是简单易用，不需要假设随机变量的分布类型。但是，EDF 的缺点是它对样本容量非常敏感，当样本容量较小时，EDF 可能不准确。

**5.2 参数分布函数**

参数分布函数是假设随机变量服从某种已知的分布类型，然后根据给定的数据估计分布的参数。常用的参数分布函数包括正态分布、指数分布、泊松分布等。

参数分布函数的计算公式因分布类型而异。例如，正态分布的参数分布函数如下：

f(x) = (1 / (σ * √(2π))) * exp(-(x - μ)^2 / (2σ^2))

其中：

* f(x) 是正态分布的概率密度函数
* μ 是正态分布的均值
* σ 是正态分布的标准差

参数分布函数的优点是它可以对随机变量的分布进行准确的描述。但是，参数分布函数的缺点是它需要假设随机变量的分布类型，如果假设错误，则建模结果可能会不准确。

**5.3 贝叶斯分布函数**

贝叶斯分布函数是基于贝叶斯定理建立的概率分布函数。贝叶斯定理的公式如下：

P(A | B) = P(B | A) * P(A) / P(B)

其中：

* P(A | B) 是在已知事件 B 发生的情况下，事件 A 发生的概率
* P(B | A) 是在已知事件 A 发生的情况下，事件 B 发生的概率
* P(A) 是事件 A 的先验概率
* P(B) 是事件 B 的概率

贝叶斯分布函数的优点是它可以结合先验知识和数据信息来估计随机变量的分布。但是，贝叶斯分布函数的缺点是它需要指定先验分布，如果先验分布选择不当，则建模结果可能会不准确。