【股市预测实战】：LSTM模型的理论基础与应用演练

# 1. 股市预测的理论基础

在资本市场中，股市预测一直是一个充满挑战的课题。投资者和分析师寻求通过各种方法来预测股票价格的走势，以期获得超额收益。然而，股市价格受到众多因素的影响，包括经济数据、公司财报、政策调整、市场情绪等，这使得股市预测变得异常复杂。从理论角度来看，股市价格变动可以被看作是一个时间序列问题，即每一个新的价格点都是基于历史价格信息及其他可能的解释变量得出的。

股市预测理论基础的关键在于理解市场行为的模式和规律。这些模式可能包括趋势、周期性波动、季节性变化等，而规律则是指市场参与者行为的可预测性。为了捕捉这些模式和规律，投资者和研究人员通常会采用统计学和机器学习的技术，而近年来，深度学习特别是LSTM（长短期记忆网络）因其在时间序列预测方面的优越性能，成为了一个非常热门的研究方向。

然而，股市预测并非万无一失，市场是高度动态和不确定的。这意味着，尽管我们可以通过技术分析和统计方法来预测价格趋势，但预测的准确性始终存在限制。因此，在利用股市预测模型辅助投资决策时，需要具备对风险的充分认识和谨慎的态度。

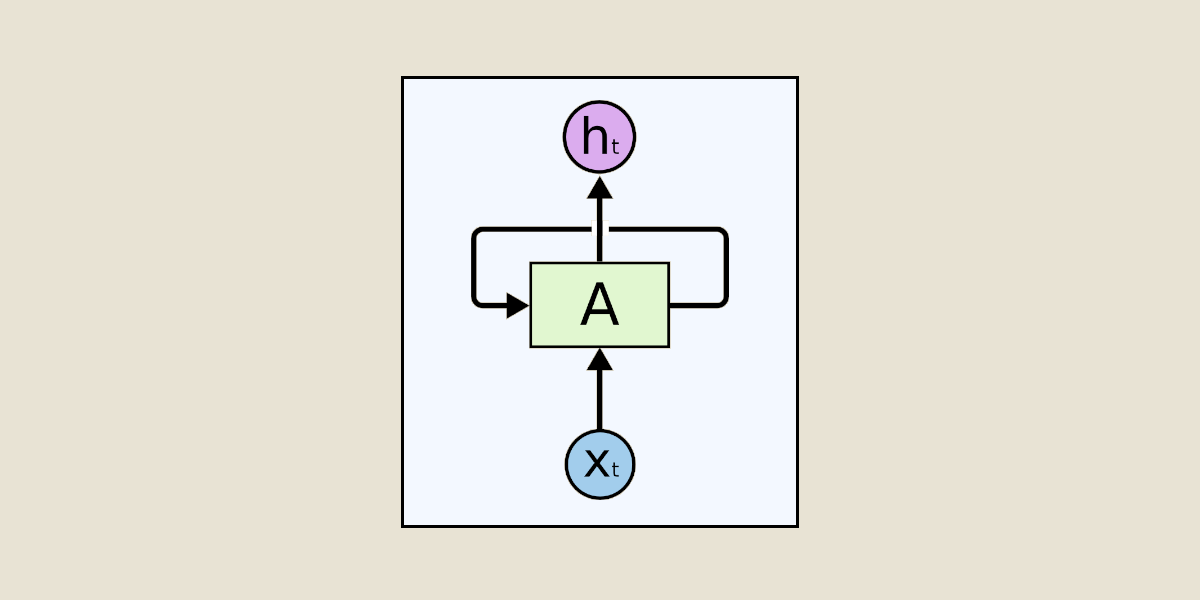
# 2. LSTM模型的原理与结构

### 2.1 LSTM模型的概念解析

#### 2.1.1 循环神经网络(RNN)简介

循环神经网络（Recurrent Neural Networks, RNNs）是一种专为处理序列数据设计的神经网络。它不同于传统的前馈神经网络，能够处理任意长度的输入序列。RNN的网络结构中包含循环，允许信息从一个步骤传递到下一个步骤，这样的设计使得网络能够记忆先前的信息，并在当前步骤中利用这些信息。

RNN的一个关键特性是它具有隐藏状态（hidden state），这个状态在序列的不同时间步之间传递，类似于短期记忆。RNN在理论上可以对任意长的序列数据建模，但实际上它在处理长距离依赖关系时存在困难，如梯度消失或梯度爆炸问题。

#### 2.1.2 LSTM的创新点和优势

长短期记忆网络（Long Short-Term Memory，LSTM）是对传统RNN的一种改进。它通过引入一种复杂的“门”结构来调节信息流，从而解决了传统RNN在长序列上训练时遇到的难题。LSTM的核心在于它能够有效地捕捉长距离依赖关系，这使得它在许多序列处理任务上表现优越。

LSTM的创新点主要体现在以下几个“门”结构：
- 输入门（input gate）：负责控制新输入信息的加入。
- 遗忘门（forget gate）：决定保留或丢弃某些信息。
- 输出门（output gate）：决定输出哪些信息。

这些门通过训练学习何时开放或关闭，允许信息流入或流出，有效地解决了梯度消失的问题，并且能够长期保持信息。

### 2.2 LSTM的工作机制

#### 2.2.* 单元状态和门控机制

LSTM网络的每一层包含多个隐藏状态（通常表示为h_t），以及一个单元状态（通常表示为c_t）。单元状态在整个序列中传递，它携带了网络从序列中学习到的信息。门控机制是通过“门”结构对单元状态进行更新。

- 输入门决定哪些新信息应该被更新到单元状态。
- 遗忘门确定哪些旧信息需要从单元状态中丢弃。
- 输出门控制哪些信息将被输出到网络的隐藏状态，之后用于预测或进一步的计算。

这种设计使得LSTM能够在长期序列中保持信息，同时也有选择地忽略不重要的信息，保证了网络的长期记忆能力和过滤噪音的能力。

# 以下代码展示了使用Keras构建LSTM模型的一个简单例子
from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(timesteps, input_dim)))
model.add(LSTM(50, return_sequences=False))
model.add(Dense(1))
***pile(optimizer='adam', loss='mean_squared_error')

#### 2.2.2 时间步长的处理过程

LSTM网络通过时间步长的循环迭代处理序列数据。在每个时间步，网络读取输入序列的一部分，并基于当前的输入和前一个隐藏状态来计算新的隐藏状态。单元状态在时间步长间被传递，并根据门控机制进行更新。

在时间步长的处理过程中，遗忘门首先会确定在单元状态中需要“忘记”的信息。接着，输入门会决定新的输入信息中的哪些部分应该被加入到单元状态中。最后，输出门会决定哪些信息将被用于当前时间步的输出。

#### 2.2.3 梯度消失和梯度爆炸问题

梯度消失和梯度爆炸是深度学习中的两个主要问题。梯度消失会导致网络权重更新非常缓慢，导致网络难以学习长期依赖关系；梯度爆炸则会导致权重更新过大，网络可能会发散。

LSTM通过其门控机制减少了梯度消失问题，因为它允许梯度通过网络流动不受阻碍。然而，当数据具有高度相关的长期依赖性时，梯度仍然可能爆炸。为此，可以采用梯度裁剪（gradient clipping）或权重正则化（如L2正则化）来缓解这个问题。

### 2.3 LSTM模型的数学基础

#### 2.3.1 前向传播和反向传播算法

LSTM的前向传播过程中，网络根据当前时间步的输入数据以及前一时间步的隐藏状态和单元状态，经过门控机制后计算出当前时间步的隐藏状态和单元状态。这构成了网络对输入序列的内部表达。

LSTM的反向传播通过时间（Backpropagation Through Time, BPTT）算法对整个序列进行处理。在BPTT中，误差梯度将沿着时间步反向传播，用于更新网络的权重。这是通过链式法则来实现的，逐层计算每一步的误差梯度，并对权重进行更新。

# 以下是一个简单的LSTM网络训练过程的伪代码
for epoch in range(num_epochs):
    for X, y in training_data:
        # X是输入序列，y是目标数据
        model.forward(X)  # 前向传播
        loss = loss_function(model.output, y)  # 计算损失
        model.backward(loss)  # 反向传播
        model.update_weights()  # 更新权重

#### 2.3.2 损失函数和优化器的选择

在训练LSTM模型时，选择合适的损失函数和优化器至关重要。损失函数用于评估模型预测值与真实值之间的差异，常见的损失函数包括均方误差（MSE）和交叉熵损失。

优化器则负责调整模型的权重，以最小化损失函数的值。常见的优化算法包括随机梯度下降（SGD）、Adam优化器、RMSprop等。不同的优化器有不同的优势，例如Adam优化器结合了RMSprop和动量（Momentum）的思想，能够在训练中自适应地调整学习率，并且对梯度进行校正。

选择优化器时需要考虑其稳定性和对特定问题的适应性。在实践中，Adam优化器因为其良好的性能和易用性，通常是训练深度学习模型的首选。

# 以下是一个使用Keras进行模型编译的例子，展示了损失函数和优化器的选择
***pile(
    optimizer='adam',  # 选择优化器
    loss='mean_squared_error'  # 选择损失函数
)

在下一章节中，我们将进一步讨