【从RNN到LSTM】：递归神经网络的演变与创新突破

# 1. 递归神经网络(RNN)基础

在理解复杂的机器学习模型之前，我们首先需要从最基础的概念开始。递归神经网络（Recurrent Neural Network，简称RNN）是一种深度学习网络，特别适合处理序列数据。RNN的设计让网络具有记忆功能，使其在处理数据时能够考虑之前的信息，这对于时间序列分析、语言模型等任务至关重要。

## 1.1 RNN的基本概念

RNN之所以得名，是因为它在处理序列数据时采用的是循环的方式，每个时间步的输出都会作为下一个时间步的输入之一。这意味着网络可以从以往的经历中学习，并利用这些信息影响后续决策。RNN的这种设计在理论上赋予了它处理任意长度序列的能力。

## 1.2 RNN在序列处理中的应用

RNN的应用场景非常广泛，它不仅可以用于语音识别、自然语言处理等领域，还可以用于机器翻译、图像描述等复杂的任务。例如，在语音识别中，RNN能够根据上下文中的声音模式来识别单词；在自然语言处理中，RNN可以用于预测下一个词的出现。

接下来的章节将深入探讨RNN的工作原理和架构，并了解其数学基础、训练技巧，以及在实践中遇到的优化和挑战。

# 2. RNN的理论架构与发展

## 2.1 RNN的工作原理

### 2.1.1 RNN的时间序列处理

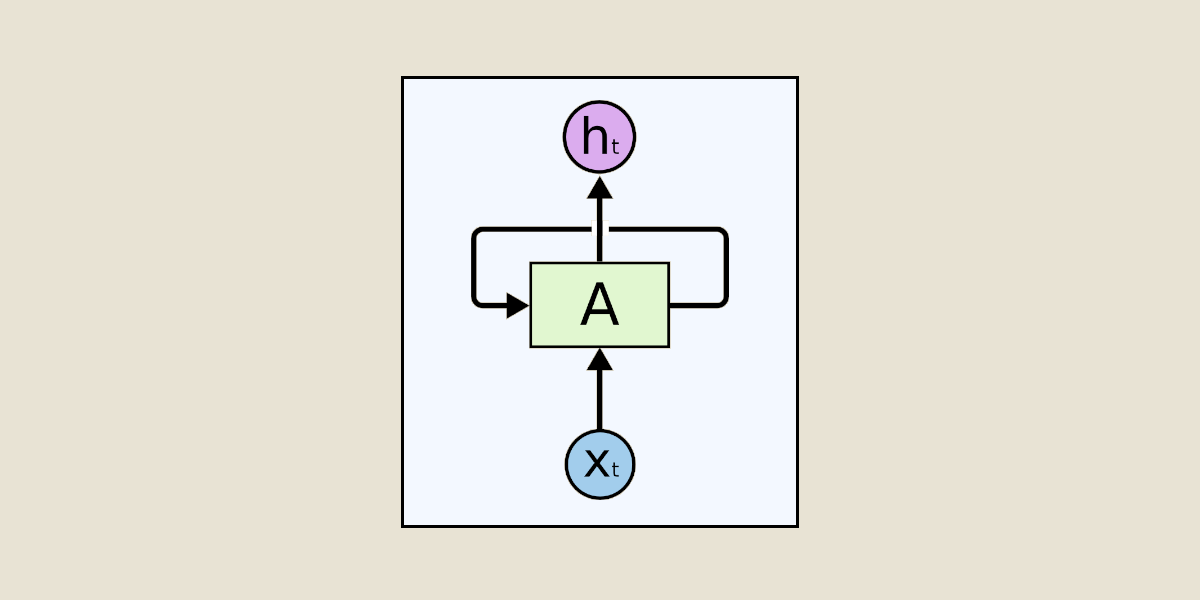
递归神经网络（RNN）是一种专门处理序列数据的神经网络，能够利用其内部的循环机制来处理任意长度的序列。不同于传统全连接神经网络只能处理固定大小的输入，RNN通过在时间上展开能够处理序列数据。每个时间步接受当前的输入以及前一时间步的隐藏状态作为输入，并产生当前时间步的隐藏状态和输出。

这种设计使得RNN特别适合于自然语言处理和时间序列分析等领域，比如语言模型、机器翻译、语音识别等。时间序列处理是RNN的重要应用之一，无论是文本中的单词序列还是时间序列中的观测数据，RNN都能够利用其隐藏层状态来进行信息的整合和预测。

### 2.1.2 循环与反馈机制

RNN的核心在于它的循环和反馈机制，循环允许信息在时间步间流动，反馈则使得网络能够从其自身的输出中学习，从而形成反馈循环。RNN的这种结构可以看作是同一个神经网络在不同时间步的复制，这些复制网络共享权重参数，但拥有不同的输入和状态。

在训练过程中，梯度通过时间反向传播（Backpropagation Through Time, BPTT），这个过程中梯度必须在时间步之间流动，可能导致梯度消失或梯度爆炸的问题。梯度消失问题使得网络难以学习到长期依赖关系，而梯度爆炸则可能导致权重更新过大，使得网络难以稳定训练。

## 2.2 RNN的数学基础

### 2.2.1 权重矩阵与激活函数

在RNN的数学模型中，权重矩阵是连接前一状态和当前状态以及输入和当前状态的重要组成部分。权重矩阵的作用相当于一个参数化的转换，将输入和前一状态的信息进行线性变换，而激活函数则负责引入非线性因素，使得RNN能够学习复杂的模式。

对于每个时间步，RNN的计算可以表示为以下形式：

h_t = f(W * h_{t-1} + U * x_t + b)

其中 `h_t` 是当前时间步的隐藏状态，`h_{t-1}` 是前一时间步的隐藏状态，`x_t` 是当前时间步的输入，`W` 和 `U` 是权重矩阵，`b` 是偏置项，而 `f` 是激活函数，比如双曲正切（tanh）或ReLU函数。

### 2.2.2 梯度消失和梯度爆炸问题

梯度消失问题通常是由于激活函数在输入较大时饱和导致的导数非常小，这使得在BPTT过程中梯度随着反向传播逐渐衰减，导致RNN在学习过程中难以捕捉到长距离的依赖关系。另一方面，梯度爆炸问题通常是由于梯度在反向传播过程中被放大，导致权重更新不稳定，可能会引起模型训练的发散。

为了解决这些问题，研究人员提出了多种策略，例如使用ReLU及其变种作为激活函数，以及使用梯度剪切、权重正则化和改进的优化算法（如Adam优化器）。

## 2.3 RNN的训练技巧

### 2.3.1 序列长度的处理方法

处理不同长度的序列是RNN训练中常见的问题。一种常用的方法是使用填充（padding）和掩码（masking）技术，它们可以保证不同长度的序列能够被统一地处理。填充是指在较短的序列末尾添加特定值（如0）来补齐到与其他序列相同的长度。掩码则是在计算损失时避免将填充部分考虑进去。

### 2.3.2 权重初始化策略

权重的初始化方法对模型的训练速度和收敛性有重要影响。对于RNN，合适的初始化方法可以缓解梯度消失和梯度爆炸问题。常见的权重初始化策略包括Xavier初始化（也称为Glorot初始化）和He初始化。Xavier初始化可以使得权重在初始化时保持较小的方差，而He初始化则用于ReLU激活函数，有助于减少梯度消失。

### 2.3.3 正则化技术的应用

正则化技术，如L1和L2正则化，可以防止模型过拟合，提高模型的泛化能力。对于RNN，还可以使用dropout技术作为正则化的一种形式。在RNN中，dropout可以通过在每个时间步随机丢弃一部分神经元来防止模型对特定时间步的输入过度依赖。

### 代码块示例

import numpy as np

def simple_rnn_cell(input, prev_hidden, Wx, Wh, b):
    """
    Simple RNN Cell implementation
    input: the input vector (shape: [input_size])
    prev_hidden: the previous hidden state (shape: [hidden_size])
    Wx: input-to-hidden weights (shape: [input_size, hidden_size])
    Wh: hidden-to-hidden weights (shape: [hidden_size, hidden_size])
    b: bias vector (shape: [hidden_size])
    """
    hidden = np.tanh(np.dot(Wx, input) + np.dot(Wh, prev_hidden) + b)
    return hidden

# Example weights and bias initialization
input_size = 10
hidden_size = 20
Wx = np.random.randn(hidden_size, input_size) * 0.01  # small random numbers
Wh = np.random.randn(hidden_size, hidden_size) * 0.01
b = np.zeros((hidden_size,))

# Example usage
input_vector = np.random.randn(input_size)
prev_hidden_state = n