优化模型性能：MATLAB中的随机森林特征工程，释放数据潜力

# 1. MATLAB中的随机森林简介**

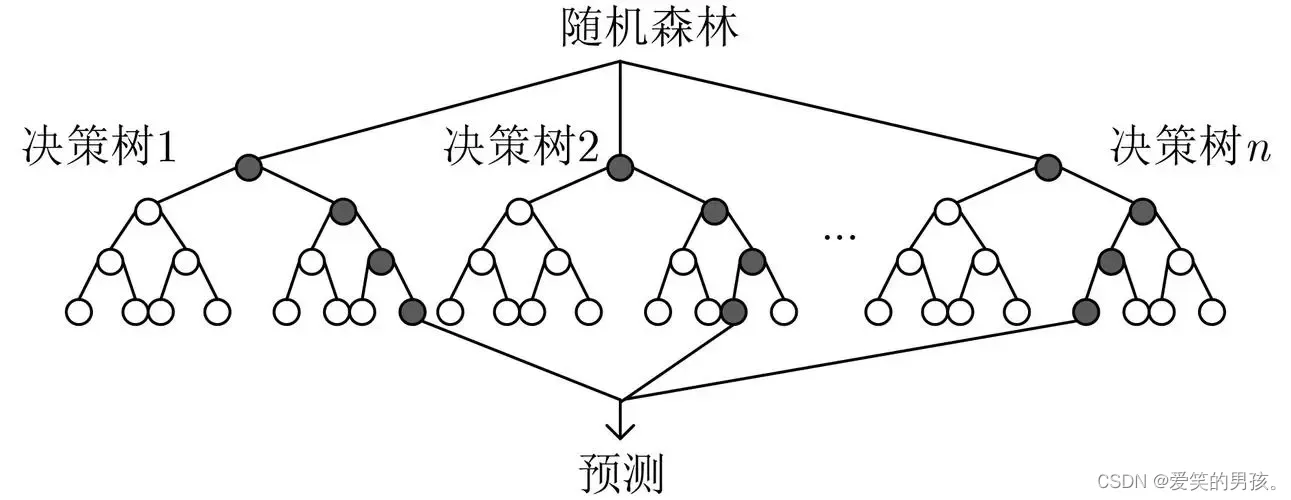
随机森林是一种强大的机器学习算法，它通过构建多棵决策树来实现预测。在MATLAB中，使用随机森林进行分类和回归任务非常方便。本节将介绍随机森林的基本概念，包括其工作原理、优势和局限性。

MATLAB提供了一系列用于构建和评估随机森林模型的函数。这些函数允许用户指定树的数量、树的深度以及其他超参数。通过调整这些超参数，可以优化模型的性能并提高其预测准确性。

# 2. 随机森林特征工程理论

### 2.1 变量重要性评估

变量重要性评估是确定哪些特征对模型预测最具影响力的过程。在随机森林中，有两种常用的重要性度量：

**2.1.1 Gini重要性**

Gini重要性衡量的是一个特征在减少节点不纯度方面的作用。对于一个节点，其不纯度可以用Gini系数来衡量：

Gini(p) = 1 - Σp_i^2

其中，p_i是节点中第i类的概率。

当一个特征被用来分割节点时，它会产生两个子节点。Gini重要性计算为原始节点不纯度与分割后的子节点不纯度的减少量之和：

Importance(feature) = Σ(Gini(parent) - Gini(left_child) - Gini(right_child))

**2.1.2 信息增益**

信息增益衡量的是一个特征在减少节点熵方面的作用。对于一个节点，其熵可以用信息熵来衡量：

Entropy(p) = -Σp_i * log(p_i)

当一个特征被用来分割节点时，它会产生两个子节点。信息增益计算为原始节点熵与分割后的子节点熵的减少量之和：

Gain(feature) = Entropy(parent) - (Entropy(left_child) * p_left + Entropy(right_child) * p_right)

其中，p_left和p_right是左子节点和右子节点的概率。

### 2.2 特征选择算法

特征选择算法可以帮助我们从一组特征中选择最相关的特征，从而减少模型的复杂度和提高其性能。在随机森林中，常用的特征选择算法有：

**2.2.1 递归特征消除**

递归特征消除（RFE）是一种逐步向后的特征选择算法。它从使用所有特征的模型开始，然后迭代地删除对模型预测贡献最小的特征。

from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier

# 创建随机森林分类器
clf = RandomForestClassifier()

# 创建RFE特征选择器
selector = RFE(clf, n_features_to_select=10)

# 拟合特征选择器
selector.fit(X, y)

# 获取选定的特征索引
selected_features = selector.support_

**2.2.2 L1正则化**

L1正则化是一种惩罚特征系数绝对值之和的正则化方法。它可以帮助我们选择稀疏模型，即具有较少非零系数的模型。

from sklearn.linear_model import LogisticRegression

# 创建带L1正则化的逻辑回归分类器
clf = LogisticRegression(penalty='l1')

# 拟合分类器
clf.fit(X, y)

# 获取选定的特征索引
selected_features = np.where(clf.coef_ != 0)[1]

# 3.1 数据预处理

数据预处理是特征工程的重要一步，可以提高模型的性能。对于随机森林模型，常见的预处理步骤包括：

#### 3.1.1 缺失值处理

缺失值的存在会影响模型的训练和预测。处理缺失值的方法有多种，包括：

- **删除缺失值：**如果缺失值较少，可以将其删除。
- **用平均值或中位数填充：**如果缺失值较多，可以用该特征的平均值或中位数填充。
- **用k近邻法填充：**用缺失值相邻的k个样本的平均值或中位数填充。

#### 3.1.2 数据归一化

数据归一化可以消除特征之间的量纲差异，使模型更易于训练。常用的归一化方法包括：

- **最小-最大归一化：**将特征值映射到[0, 1]区间内。
- **标准化：**将特征值减去均值并除以标准差。

import numpy as np

# 最小-最大归一化
data_normalized = (data - np.min(data)) / (np.max(data) - np.min(data))

# 标准化
data_normalized = (data - n