数据压缩算法实战：Huffman编码与LZW算法详解

# 1. 第一章 数据压缩算法概述

随着信息技术的飞速发展，数据的生成和存储呈爆炸式增长。数据压缩技术作为信息处理的关键组成部分，在减少存储空间需求和提高数据传输效率方面发挥着重要作用。本章将带您了解数据压缩算法的基本概念、原理及其在现代计算中的重要性，为深入学习后续章节中具体算法的实现和应用打下坚实的理论基础。

# 2. Huffman编码的理论基础与实现

## 2.1 Huffman编码原理

### 2.1.1 编码过程分析

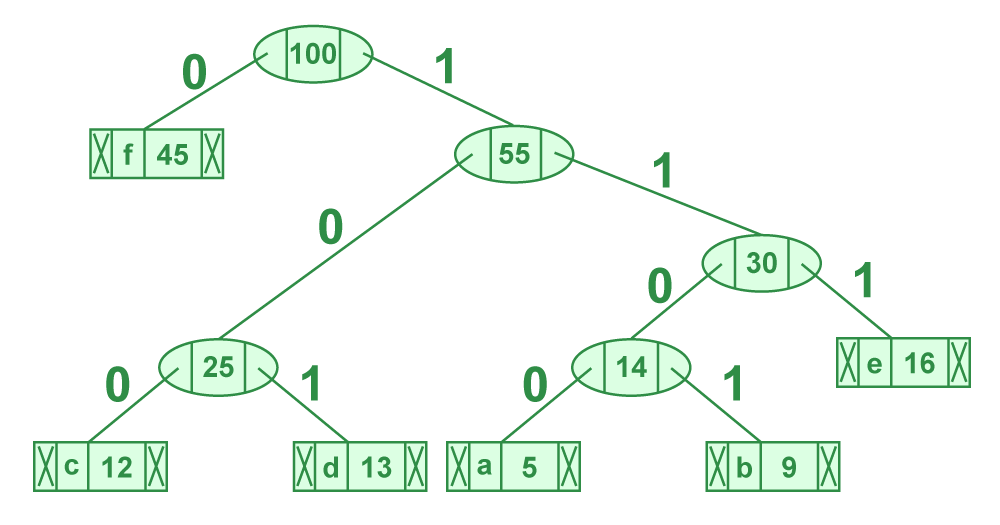
Huffman编码是一种广泛使用的数据压缩技术，它基于字符出现的频率来构建最优的前缀编码。编码过程首先需要统计每个字符的频率，然后根据频率构建一棵Huffman树。树的构造过程是一个贪心算法，总是选择两个频率最低的节点合并成一个新节点，新节点的频率是两个子节点频率之和。这个过程一直进行，直到只剩下一个节点，这个节点就是Huffman树的根节点。

具体的编码过程涉及从Huffman树的根节点开始，为每个字符创建一条从根到叶的路径。如果路径是向左走的，就用二进制的"0"表示；如果向右，就用"1"表示。最终每个字符都会对应一个唯一的二进制编码。

### 2.1.2 编码效率的数学证明

Huffman编码的效率可以从信息论的角度进行数学证明。根据Shannon的定理，一个字符的编码长度应该接近其信息熵。Huffman编码正是基于这种思想，通过构建最优二叉树确保了低频字符有较长的编码，高频字符有较短的编码。

数学上，我们可以证明Huffman编码的期望编码长度小于或等于任何其他前缀编码的期望长度。给定一个字符集，以及每个字符的概率分布，Huffman树能确保得到最小的加权路径长度（WPL）。WPL是所有字符编码长度与其概率乘积之和，这个值越小，编码效率越高。

## 2.2 Huffman树的构建与优化

### 2.2.1 树的构建方法

构建Huffman树的基本方法涉及一系列步骤，其核心在于重复执行两个节点的合并操作。以下是具体的步骤：

1. 统计字符集中的每个字符及其出现的频率。
2. 创建一个优先队列（最小堆），并将所有字符作为叶子节点加入队列，频率作为优先级。
3. 当优先队列中有多于一个节点时，重复以下步骤：
- 从队列中取出两个频率最低的节点。
- 创建一个新的内部节点作为它们的父节点，其频率为两个子节点频率之和。
- 将新创建的内部节点加入优先队列。
4. 当优先队列中只剩下一个节点时，这个节点就是Huffman树的根节点。

### 2.2.2 权值调整与压缩性能优化

在某些特殊的应用场景下，需要对Huffman树进行权值调整以优化压缩性能。例如，对于文本数据，高频出现的字符（如字母 'e'）可能需要有更短的编码。为了达到这个目的，可以给特定字符赋予人为的高频权重，或者在构建树之前对字符频率进行归一化处理。

此外，还可以通过调整字符编码的起始点来优化压缩效率。比如，可以将所有编码的长度对齐到某个特定的值，从而简化解码过程。

## 2.3 Huffman编码的实际应用

### 2.3.1 文件压缩的实现步骤

为了应用Huffman编码进行文件压缩，需要遵循以下步骤：

1. 读取文件并计算字符出现的频率。
2. 利用字符频率构建Huffman树。
3. 根据Huffman树为每个字符生成编码。
4. 遍历文件，使用生成的Huffman编码替换原文中的字符。
5. 将Huffman树和编码后的数据一起输出到新的文件中。

在这个过程中，Huffman树的结构需要以某种形式存储，以便在解压缩时重建树结构。通常的做法是采用某种前序遍历方法记录树的结构和权重。

### 2.3.2 编码与解码的程序实现

下面的伪代码展示了Huffman编码和解码的基本逻辑：

function buildHuffmanTree(char频率表) {
    // 根据字符频率构建Huffman树的逻辑
}

function HuffmanEncode(inputFile, outputFile) {
    // 统计字符频率
    char频率表 = 计算频率(inputFile)
    // 构建Huffman树
    Huffman树 = buildHuffmanTree(char频率表)
    // 根据Huffman树生成编码表
    编码表 = 生成编码表(Huffman树)
    // 读取文件并用Huffman编码替换字符
    encodedData = []
    for character in inputFile {
        编码表.append(Huffman编码(character))
    }
    // 写入编码后的数据及Huffman树到输出文件
    outputFile.write(编码表)
    outputFile.write(encodedData)
}

function HuffmanDecode(inputFile, outputFile) {
    // 读取编码表和Huffman树
    编码表, Huffman树 = 从inputFile读取
    // 从Huffman树解码数据
    decodedData = []
    currentTreePosition = Huffman树的根节点
    for bit in inputFile {
        if bit == "0" {
            currentTreePosition = currentTreePosition.left
        } else {
            currentTreePosition = currentTreePosition.right
        }
        if currentTreePosition 是叶子节点:
            decodedData.append(当前叶子节点的字符)
            currentTreePosition = Huffman树的根节点
    }
    // 写入解码后的数据到输出文件
    outputFile.write(decodedData)
}

实际的编码与解码实现需要考虑存储结构、错误处理、效率优化等多个方面。上述伪代码仅为逻辑层面的描述。在编程实现时，还需要考虑数据类型转换、文件I