图论基础与应用大揭秘：网络流与最短路径算法详解

# 1. 图论基础概述

图论是数学的一个分支，它研究的是由对象以及它们之间的关系构成的图形。在计算机科学和IT领域，图论的重要性体现在各种网络和复杂系统的建模中，比如社交网络分析、网络设计和优化、互联网流量的路由选择等。

## 1.1 图的定义与组成

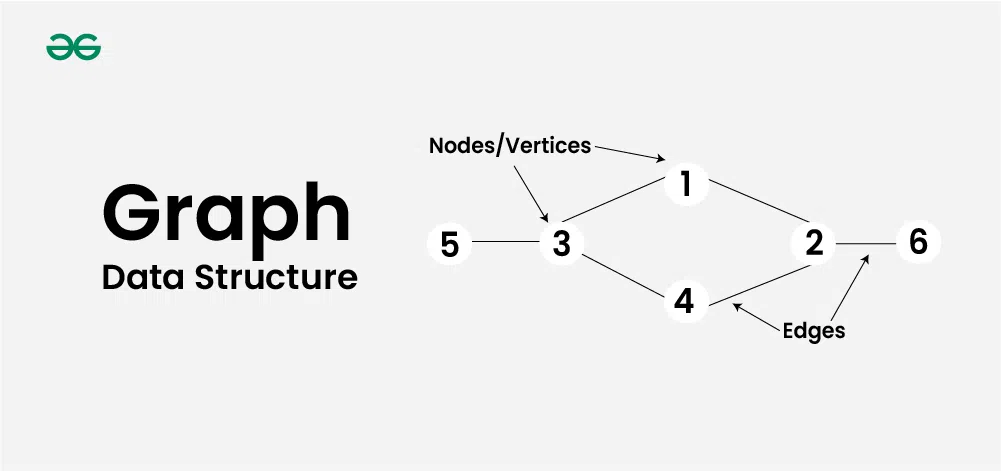
在图论中，一个**图**（Graph）G由两部分组成，顶点的集合V(G)和边的集合E(G)。边连接着顶点，并且可以是有方向的，这种图被称为**有向图**；如果边是没有方向的，则为**无向图**。

graph LR
    A((A)) ---|label| B((B))

在这个示例中，A和B是顶点，而它们之间的连接线表示边。如果这条线是有方向的，则表示从A指向B。

## 1.2 图的基本术语

在图论中，我们经常遇到的术语包括路径（path）、回路（circuit）、连通图（connected graph）等。**路径**指的是从一个顶点到另一个顶点经过的边的序列。如果路径的第一个顶点和最后一个顶点是同一个顶点，那么这样的路径称为**回路**。当一个图中任意两个顶点都是连通的，即存在路径相连，这样的图称为**连通图**。

## 1.3 图的应用实例

图论的概念和算法广泛应用于网络设计和优化。例如，在设计最短路径的算法时，可以采用图论中的Dijkstra算法或Floyd-Warshall算法来找到两点之间最短的路径。在社交网络分析中，图论可以帮助我们理解人与人之间的关系，比如衡量信息传播的效率和社区的形成。

图论不仅在理论上有深厚的根基，在实际应用中也显示出巨大的价值，它是我们分析和解决现实世界问题的强大工具。接下来的章节中，我们将深入探讨网络流算法和最短路径算法等图论中的核心内容。

# 2. 网络流算法深入剖析

## 2.1 网络流理论基础

### 2.1.1 流网络的定义与性质

流网络是一种特殊的有向图，其每一条边都有一个与之相关联的容量（capacities）上限，代表在该边能够通过的最大流量。在网络流问题中，我们通常关注的是从一个特定的源点（source）到一个特定的汇点（sink）的最大流量问题。流网络中的每个节点都有一个流入流量和流出流量的平衡性，即进入节点的流量总和等于离开节点的流量总和，这种性质称为流守恒（conservation of flow）。

流网络在数学上可以被形式化为一个五元组G=(V,E,c,s,t)，其中V是顶点集合，E是有向边集合，c是容量函数，s是源点，t是汇点。在实际应用中，流网络可以用来模拟通信网络中的数据传输，交通网络中的车辆流动，或者供应链中的商品流动。

一个典型的流网络可以用以下的mermaid流程图表示：

graph TD
    A[源点] -->|10| B[节点1]
    B -->|4| C[节点2]
    B -->|8| D[节点3]
    C -->|9| E[汇点]
    D -->|10| E

在这个例子中，我们可以看到源点A有一个固定的出流量和汇点E有一个固定的入流量，而其他节点都遵循流守恒原则。

### 2.1.2 最大流问题的数学表述

最大流问题的目标是找到从源点到汇点的最大流量，同时满足边上的容量限制以及流守恒性质。用数学表达式来说，对于流网络G=(V,E,c,s,t)，我们希望找到一个流量函数f，使得对于任意边(u,v)∈E，有f(u,v)≤c(u,v)（容量限制），并且对于除了源点s和汇点t之外的任意节点v∈V，流入v的流量总和等于流出v的流量总和（流守恒）。

最大流f*的值定义为所有从源点出发的边的流量之和，即f*(s,v)（对于任意v∈V）。寻找最大流的问题是一个典型的优化问题，在运筹学、网络科学和计算机科学中有着广泛的应用。

## 2.2 网络流的经典算法

### 2.2.1 Ford-Fulkerson方法

Ford-Fulkerson方法是一种基于增广路径思想的算法，用于计算网络流中从源点到汇点的最大流量。基本思想是重复寻找增广路径，并在找到的增广路径上增加流量，直到无法再找到增广路径为止，此时的流量即为最大流。

在寻找增广路径的过程中，算法通过不断调整流量f(u,v)，尝试增加从源点到汇点的流量。当一条路径上的反向边容量允许流量反向流动时，这条路径就可以视为增广路径，然后将这条路径上的最小剩余容量加到流上。

以下是使用伪代码描述的Ford-Fulkerson方法：

function FordFulkerson(G, s, t):
    f = 0
    while there is a path p from s to t in G残量网络(G, f):
        c_f = min{c(u,v) - f(u,v) | (u,v) in p}
        for each edge(u,v) in p:
            f(u,v) = f(u,v) + c_f
            f(v,u) = f(v,u) - c_f
    return f

在实际操作中，残量网络是由原网络在当前流量函数f的基础上构造出来的，用于在每次迭代中寻找增广路径。

### 2.2.2 Edmonds-Karp算法详解

Edmonds-Karp算法是Ford-Fulkerson方法的一个实现，它使用广度优先搜索（BFS）来寻找增广路径。该算法保证每次寻找的增广路径都是最短的，这在一定程度上减少了循环次数，提高了算法效率。

Edmonds-Karp算法特别强调了在每次寻找增广路径时都使用BFS，而不是其他图搜索方法。这不仅简化了算法的实现，而且保证了算法的时间复杂度为O(VE^2)，其中V是顶点数，E是边数。Edmonds-Karp算法是多项式时间复杂度的，因此它适用于实际问题中的大规模图。

伪代码如下：

function EdmondsKarp(G, s, t):
    f = FordFulkerson(G, s, t)
    while there is a path p from s to t in G残量网络(G, f):
        c_f = min{c(u,v) - f(u,v) | (u,v) in p}
        for each edge(u,v) in p:
            f(u,v) = f(u,v) + c_f
            f(v,u) = f(v,u) - c_f
    return f

### 2.2.3 Dinic算法及其优化

Dinic算法是另一种寻找最大网络流的算法，它比Edmonds-Karp算法更加高效。Dinic算法的主要特点是它引入了“层次图”的概念，来减少寻找增广路径时的搜索范围。层次图是一个将节点分为不同层次的图，其中源点位于第一层，汇点位于最后一层，其他节点按照距离源点的最短路径长度划分层次。

Dinic算法在每次迭代中构建层次图，并且仅在这个层次图中寻找增广路径。如果无法找到增广路径，则通过调整某些边的流量来更新层次图，从而进一步寻找增广路径。

Dinic算法的时间复杂度为O(V^2*E)，它在大多数情况下比Edmonds-Karp算法更优，但实现相对复杂。以下是Dinic算法的伪代码：

function Dinic(G, s, t):
    while true:
        level_graph = 构建层次图(G, s,