回溯算法深度解析：八皇后问题与数独求解策略

# 1. 回溯算法基础

回溯算法是一种通过探索所有可能的候选解来找出所有解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会通过在上一步进行一些变化来丢弃它，即回溯并且再次尝试。回溯算法采用试错的思想，尝试分步去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其他的可能的分步解答再次尝试寻找问题的答案。

在编程中，回溯算法常用于解决约束满足问题，如八皇后问题、图的着色、旅行商问题等。它通过递归函数来遍历所有可能的解，并通过剪枝技术来优化搜索过程，从而提高算法效率。

接下来的章节中，我们将通过八皇后问题和数独求解两个经典的回溯算法应用，深入理解其原理和实现细节。

# 2. ```
# 第二章：八皇后问题的回溯法解析

## 2.1 八皇后问题概述

### 2.1.1 问题的起源与规则
八皇后问题（Eight Queens Puzzle）是一个经典的算法问题，在19世纪末由国际象棋棋手马克思·贝瑟尔提出。问题的目标是在一个8×8的国际象棋棋盘上放置八个皇后，使得它们互不攻击，即任意两个皇后都不在同一行、同一列或同一对角线上。这个问题在数学上归类为组合数学的一个问题，它鼓励研究者寻找所有可能的解决方案，并且有时还会考虑问题的扩展，例如改变棋盘大小或者增加皇后数量。

### 2.1.2 回溯算法在八皇后问题中的应用
回溯算法是一种通过探索所有可能情况的算法，当发现当前解不可能满足问题的要求时，就回退一步，尝试其他可能的选择。八皇后问题就是回溯算法应用的一个典型例子。它采用递归的方式，每放置一个皇后，就递归地尝试在下一行放置另一个皇后，直到找到所有八个皇后的合法位置或者无解时回溯到上一个状态。

## 2.2 八皇后问题的算法实现

### 2.2.1 算法的数据结构设计
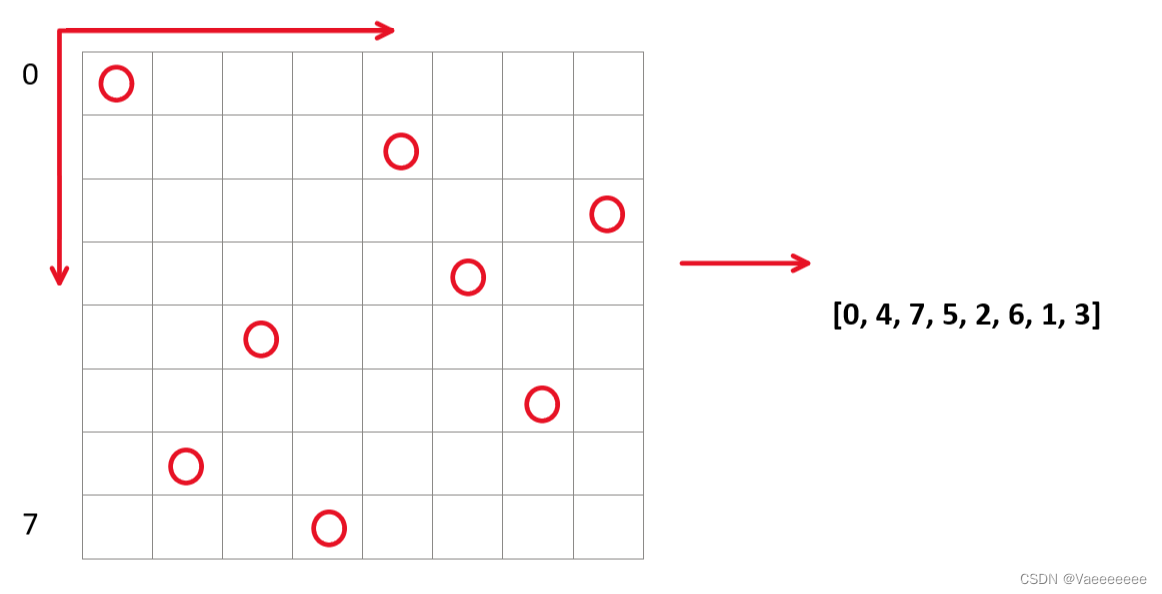
为了实现八皇后问题的回溯算法，我们需要设计合适的数据结构来存储棋盘的状态。通常我们可以使用一个一维数组`int[] board = new int[8];`来表示棋盘，其中每个数组元素的索引对应棋盘上的行，元素的值对应皇后所在的列。例如`board[i] = 4`表示第`i+1`行的皇后位于第`4+1`列。

### 2.2.2 递归函数构建与搜索过程
下面是构建八皇后问题解决方案的递归函数伪代码示例：

boolean solveNQUtil(int board[], int col) {
    if (col >= board.length) {
        return true;
    }
    for (int i = 0; i < board.length; i++) {
        if (isSafe(board, i, col)) {
            board[col] = i;
            if (solveNQUtil(board, col + 1))
                return true;
            board[col] = -1; // 回溯
        }
    }
    return false;
}

boolean isSafe(int[] board, int row, int col) {
    for (int i = 0; i < col; i++)
        if (board[i] == row || Math.abs(board[i] - row) == Math.abs(i - col))
            return false;
    return true;
}

在`solveNQUtil`函数中，`col`参数表示当前考察的列，每递归一层就尝试将皇后放在不同的行。`isSafe`函数检查当前位置是否安全，即没有其他皇后能够攻击到它。

### 2.2.3 剪枝策略的优化
为了解决八皇后问题，我们需要尽量减少搜索空间。剪枝策略是一种有效的方法，通过减少不必要的尝试来提升算法的效率。例如，如果在第`col`列，我们在第一行就发现没有合适的位置放置皇后，那么就没有必要去考察第二行、第三行等，因为后面的行肯定也没有合适的位置。

## 2.3 八皇后问题的求解演示

### 2.3.1 问题的解决方案代码展示
以下是一个完整的八皇后问题的解决方案代码示例：

public class EightQueens {
    private int[] board;

    public EightQueens(int size) {
        board = new int[size];
    }

    public boolean solve() {
        return solveNQUtil(0);
    }

    private boolean solveNQUtil(int col) {
        if (col >= board.length) {
            printSolution();
            return true;
        }
        for (int i = 0; i < board.length; i++) {
            if (isSafe(i, col)) {
                board[col] = i;
                if (solveNQUtil(col + 1)) {
                    return true;
                }
                // 回溯
            }
        }
        return false;
    }

    private boolean isSafe(int row, int col) {
        for (int i = 0; i < col; i++) {
            if (board[i] == row || Math.abs(board[i] - row) == Math.abs(i - col)) {
                return false;
            }
        }
        return true;
    }

    private void printSolution() {
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board.length; j++) {
                if (board[j] == i) {
                    System.out.print(" Q ");
                } else {
                    System.out.print(" . ");
                }
            }
            System.out.println();
        }
        System.out.println();
    }
}

###