Python堆排序与快速排序对比：揭秘高效排序算法的内部机制

# 1. 排序算法概述

排序算法是计算机科学中的基础概念，广泛应用于软件开发、数据处理、算法优化等领域。理解排序算法不仅能帮助我们快速处理数据，还能加深我们对计算机内部工作机制的认识。本章将对排序算法进行简要概述，介绍其基本分类和应用场景，为后面章节中对堆排序和快速排序更深入的探讨打下坚实的基础。

## 1.1 排序算法的基本概念

排序算法是一系列根据特定规则将一系列数据项重新排列的算法，以便按照一定的顺序（如升序或降序）排列。排序算法的效率通常由时间复杂度和空间复杂度来衡量。

## 1.2 常见排序算法分类

常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序、快速排序、堆排序等。不同算法在不同情况下有不同的表现和适用性。

## 1.3 排序算法的重要性

排序不仅能够提高数据检索的效率，还能优化数据的存储和处理。了解并掌握多种排序算法对于解决实际问题具有重要意义。

本章我们了解到排序算法是处理数据的基础工具，介绍了排序算法的基本概念、分类和重要性。接下来的章节将深入探讨堆排序和快速排序的具体理论与实现细节。

# 2. Python堆排序的理论与实现

### 2.1 堆排序算法原理

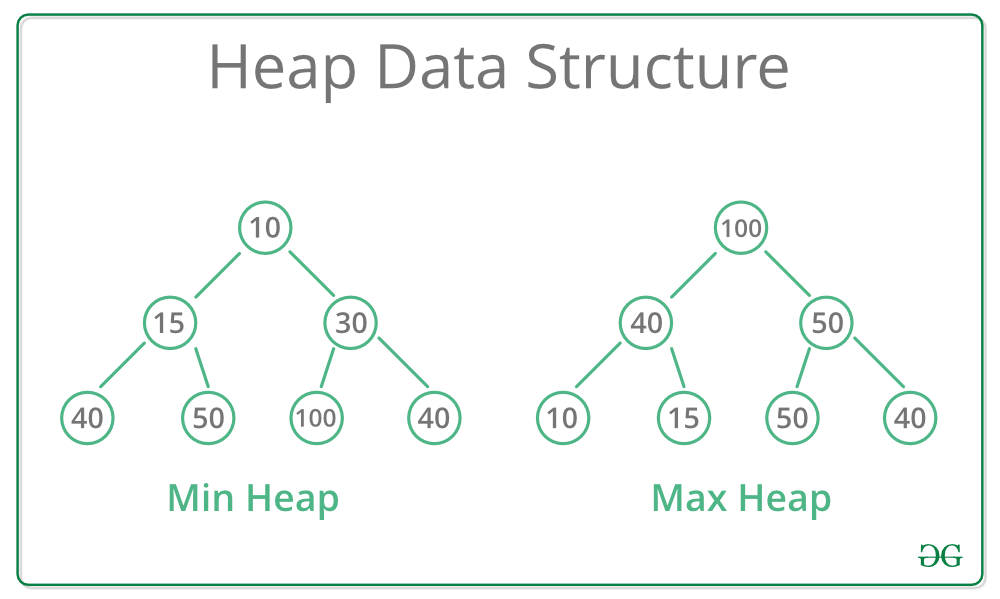
#### 2.1.1 堆的定义和性质

堆是一种特殊的完全二叉树，其每个父节点的值都必须大于或等于（对于小根堆）或小于或等于（对于大根堆）其子节点的值。在堆中，我们称父节点的值为堆的值。堆的性质保证了堆的根节点始终是堆中的最大元素或最小元素，这使得它非常适合实现优先队列。

堆通常用数组表示，对于数组中的任意位置i（i从1开始计数），其左子节点的位置为2i，右子节点的位置为2i+1，而其父节点的位置为i/2。这种存储方式允许我们通过简单的数组索引运算即可访问节点的父节点和子节点。

### 2.2 堆排序的Python实现

#### 2.2.1 构建最大堆

在堆排序算法中，构建最大堆是一个关键步骤，它保证了我们可以在O(1)时间内访问当前最大的元素。构建最大堆的过程涉及将一个无序的数组转换为最大堆。

下面是构建最大堆的Python代码示例：

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[i] < arr[left]:
        largest = left

    if right < n and arr[largest] < arr[right]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def build_max_heap(arr):
    n = len(arr)

    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

arr = [12, 11, 13, 5, 6, 7]
build_max_heap(arr)
print("Max-Heap array is: ", arr)

`heapify`函数确保从索引i开始的子树满足堆的性质。`build_max_heap`函数从最后一个非叶子节点开始，调用`heapify`函数，从而逐渐构建最大堆。

#### 2.2.2 堆调整和排序过程

堆排序主要分为两个步骤：构建最大堆和逐个移除最大元素。

一旦我们有了最大堆，就可以将堆顶元素（即最大元素）和堆的最后一个元素交换，然后减少堆的大小，并重新调整堆来恢复最大堆的性质。这个过程不断重复，直到堆的大小为1，此时数组即为排序完成的状态。

def heap_sort(arr):
    n = len(arr)

    build_max_heap(arr)

    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 交换
        heapify(arr, i, 0)

arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("Sorted array is: ", arr)

在这个`heap_sort`函数中，我们首先构建一个最大堆，然后逐个移除最大元素