Python数据结构与算法结合之道：打造更强大的数据处理引擎

# 1. Python数据结构基础

Python是一种广泛应用于数据处理、机器学习和Web开发的高级编程语言。它以其简洁的语法、强大的库支持和多用途的特性，在IT行业中占据了重要地位。在深入探讨Python在算法和数据处理方面的高级应用之前，理解Python的基础数据结构是至关重要的。

## 1.1 Python中的数据结构

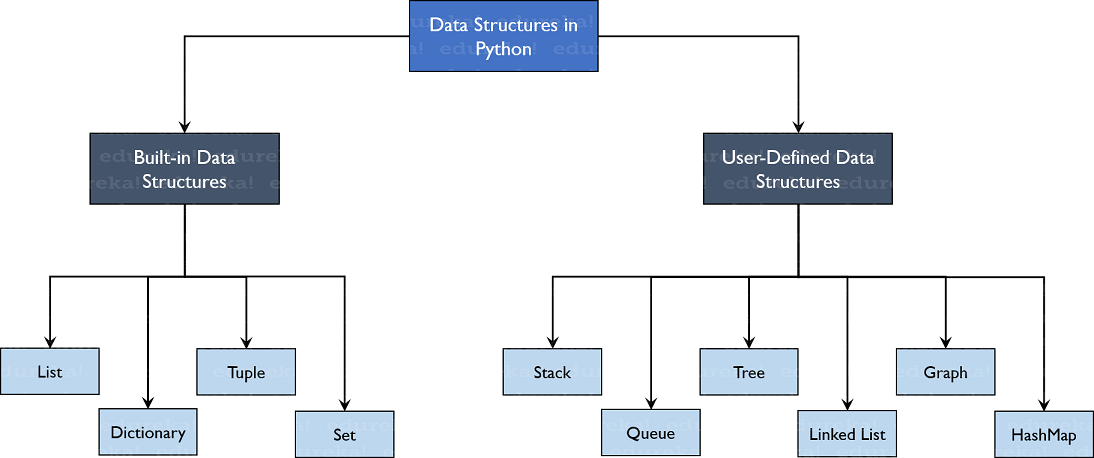
Python内置了几种基本数据类型，包括数字、字符串、布尔值、列表、元组、集合和字典。这些数据类型为存储和组织数据提供了不同的方法，它们各有其特点和应用场景：

- **列表（List）**：可变序列，支持元素添加和删除，适用于实现数组、堆栈、队列等数据结构。
- **元组（Tuple）**：不可变序列，常用于保护数据不被意外修改，或作为字典的键。
- **集合（Set）**：无序且唯一的元素集，适合进行成员资格测试和消除重复元素。
- **字典（Dictionary）**：键值对集合，通过键来存储和访问数据，适用于需要快速检索的场景。

## 1.2 高级数据结构

除了基本数据类型，Python还支持高级数据结构，例如：

- **列表推导式**：一种使用表达式来创建列表的方法，能够以简洁的方式实现复杂的操作。
- **生成器**：内存效率更高的迭代器，使用`yield`语句在函数中按需产生值。
- **集合推导式**：类似于列表推导式，但返回集合。
- **字典推导式**：创建字典的快速方式，使用键值对表达式。

理解并熟练运用这些数据结构对于编写高效和优雅的Python代码至关重要。本章的其余部分将对每种数据结构进行更深入的探讨，说明它们的内部原理、操作方法和在实际应用中的最佳实践。通过这些基础知识，读者将为进一步学习算法和数据处理技术打下坚实的基础。

# 2. 算法理论与实现

## 2.1 基础算法概念

### 2.1.1 算法的定义和重要性

算法是一组定义明确的计算步骤，用于完成特定的任务或解决某个问题。在计算机科学中，算法的概念尤为重要，因为它们是构建有效程序和系统的基础。一个算法的性能不仅直接影响程序的运行效率，而且还关系到系统是否能在合理的时间内完成计算任务。

算法的重要性体现在以下几个方面：

- **效率**：好的算法能够在最短的时间内完成任务，这对于需要实时处理的应用尤为重要。
- **资源使用**：高效的算法能够更少地使用系统资源，如内存和处理器时间，从而降低运行成本。
- **可扩展性**：随着输入规模的增加，算法的性能应该能够平滑地变化，而不是突然变得无法接受。
- **可靠性**：算法应该能够处理各种边界情况和潜在的输入错误，保证计算的稳定性。

在设计算法时，需要考虑上述因素，并对算法进行不断优化，以提高其性能和适用性。

### 2.1.2 算法的时间复杂度和空间复杂度分析

时间复杂度和空间复杂度是评价算法性能的两个重要指标。时间复杂度衡量的是算法执行时间与输入大小之间的关系，而空间复杂度则衡量算法执行过程中占用存储空间与输入大小之间的关系。

时间复杂度通常用大O表示法来描述，比如O(n)表示线性时间复杂度，O(n^2)表示二次时间复杂度。时间复杂度越低，算法的效率越高。

空间复杂度也是用类似的方式表达，它描述的是算法执行过程中占用的额外空间。

下面是一个简单的Python代码示例，计算并分析冒泡排序算法的时间复杂度和空间复杂度。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 示例数组
example_array = [64, 34, 25, 12, 22, 11, 90]
# 执行冒泡排序
sorted_array = bubble_sort(example_array)
print(sorted_array)

在上述代码中，冒泡排序算法包含两个嵌套的循环，时间复杂度为O(n^2)，其中n是数组的长度。由于冒泡排序是在原数组上进行排序的，不需要额外的存储空间，因此其空间复杂度为O(1)。

通过分析算法的时间和空间复杂度，我们可以更好地理解算法的性能瓶颈，并在此基础上进行优化。

## 2.2 排序与搜索算法

### 2.2.1 常见的排序算法及其应用场景

排序算法是将一组数据按照一定的顺序重新排列的过程。在实际应用中，不同的排序算法因其不同的时间和空间复杂度，在不同的场景下有着不同的应用。

以下是一些常见的排序算法及其应用场景：

- **冒泡排序**：简单但效率低，适用于小规模数据集的简单排序。
- **选择排序**：不稳定，每次选择最小元素与未排序部分的第一个元素交换，常用于教学演示。
- **插入排序**：在插入时进行比较和移动，适合部分有序的数据集。
- **快速排序**：分治策略，平均时间复杂度为O(n log n)，适合大规模数据集。
- **归并排序**：稳定且效率高，适合链表排序。
- **堆排序**：基于堆的结构，适合优先级队列的实现。
- **计数排序、桶排序和基数排序**：适用于特定条件下的排序，如整数排序。

每种排序算法都有其特定的使用场景，选择合适的排序算法可以显著提升程序性能。

### 2.2.2 搜索算法的分类和性能比较

搜索算法用于在数据集合中查找特定的元素或满足条件的数据项。常见的搜索算法包括线性搜索、二分搜索和深度优先搜索等。

- **线性搜索**：简单直观，适合未排序的数据集合。时间复杂度为O(n)。
- **二分搜索**：要求数据集合必须已排序，搜索效率高，时间复杂度为O(log n)。它使用分而治之的策略，每次将搜索范围减半。
- **深度优先搜索（DFS）**：用于图和树的遍历，以递归或栈实现。适用于解决路径搜索问题。

每种搜索算法都有其优缺点，通常根据数据结构的特点和应用场景来选择合适的搜索策略。

## 2.3 树与图算法

### 2.3.1 树的遍历和应用

树是一种重要的数据结构，它模拟了具有层次关系的数据。树的遍历是按一定的规则访问树中每个节点一次且仅一次的过程。

常见的树遍历算法有：

- **前序遍历**：访问根节点 -> 左子树 -> 右子树
- **中序遍历**：左子树 -> 根节点 -> 右子树
- **后序遍历**：左子树 -> 右子树 -> 根节点
- **层序遍历**：按层次从上到下逐个访问节点

树的遍历算法在诸如表达式树构建、目录文件系统遍历等领域有着广泛的应用。

### 2.3.2 图的表示方法和典型算法

图是一种复杂的数据结构，由节点（顶点）和连接节点的边组成。图的表示方法主要有邻接矩阵和邻接表。

- **邻接矩阵**：用一个二维数组来表示图中所有顶点之间的连接关系。适合顶点数量较少且稠密的图。
- **邻接表**：用链表或数组的列表来表示图中每个顶点的边集。适合顶点数量较多且稀疏的图。

图算法中，常见的有：

- **深度优先搜索（DFS）**：用于搜索或遍历图中的节点。
- **广度优先搜索（BFS）**：用于从一个顶点开始，访问所有的相邻顶点。
- **最短路径算法**：如Dijkstra算法和Floyd-Warshall算法，用于找到图中两点之间的最短路径。
- **拓扑排序**：用于有向无环图（DAG），按照边的方向排序所有顶点。

图算法在社交网络分析、网页排名（PageRank）、网络路由等领域有着非常重要的应用。

在下一章节中，我们将探讨如何将数据结构应用于算法中，进一步挖掘其潜力。

# 3. 数据结构在算法中的应用

## 3.1 列表和数组结构算法应用

### 3.1.1 列表和数组的操作技巧

列表（List）和数组（Array）是两种在算法中广泛使用的线性数据结构。列表通常是指Python中的list数据类型，它可以动态增长和缩小，且可以存储不同类型的元素。数组则通常指的是固定类型且大小固定的集合，可以是连续内存空间分配，也可以是类似列表的动态数组实现，但其元素类型相同。

在算法应用中，掌握列表和数组的操作技巧至关重要。例如，在Python中，我们经常使用append()方法向列表末尾添加元素，使用pop()方法删除列表中的最后一个元素。对于数组，则可能涉及更底层的操作，如在C语言中通过指针运算访问数组元素。此外，在算法竞赛或面试中，时间复杂度往往决定了算法的效率。因此，熟练掌握列表和数组的基本操作（如访问、插入、删除）以及它们的时间复杂度至关重要。

### 3.1.2 列表和数组在算法中的高效运用

列表和数组在算法中的高效运用表现在多个方面。例如，在处理排序问题时，数组可以利用其物理存储顺序直接进行快速排序、归并排序等高效算法。列表由于可以动态调整大小，非常适合用于实现图的邻接表表示。

以快速排序为例，我们通常采用“分而治之”的策略，即选择一个基准元素，将数组中的其他元素通过比较，根据与基准元素的大小关系，分为小于、等于和大于基准元素的三部分，递归排序左右两部分。下面是一个Python实现的快速排序示例：

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

# 示例数组
array = [3, 6, 8, 10, 1, 2, 1]
print(quicksort(array))

在这个例子中，我们首先检查数组长度，如果小于等于1，则直接返回数组，因为长度为1的数组已经是有序的。我们选取中间元素作为基准点，然后将数组分解为三部分：小于基准点的元素、等于基准点的元素和大于基准点的元素。最后递归地对左右两部分进行排序，并将排序后的结果与中间部分合并。

列表和数组的高效运用需要我们理解它们的特性，并根据算法需求合理选择。在处理需要频繁访问或修改单个元素时，数组提供了常数时间的复杂度；而在需要动态调整大小或者频繁插入和删除时，列表则更加灵活。

## 3.2 栈、队列与优先队列

### 3.2.1 栈和队列的原理及实现

栈（Stack）和队列（Queue）是两种常见的线性数据结构，它们在算法中有着广泛的应用，特别是在实现算法时可以简化逻辑。

栈是一种后进先出（LIFO）的数据结构，支持两种操作：push（添加元素到栈顶）和pop（移除栈顶元素）。栈的典型实现方式是使用数组，也可以使用链表。栈的应用场景包括函数调用栈、括号匹配、深度优先搜索（DFS）等。

队列是一种先进先出