Python堆与优先队列使用秘诀：提升数据管理与事件处理效率

# 1. 堆与优先队列的Python实现基础

在信息技术领域，堆结构和优先队列是两种极为重要的数据结构。堆结构，作为一种特殊的完全二叉树，常被用作实现优先队列。而优先队列又在诸如任务调度、数据压缩等场景中发挥着关键作用。在Python中，我们可以借助内置的`heapq`模块以及自定义类来高效实现堆与优先队列。

在接下来的章节中，我们将首先介绍堆的基本概念、性质以及在Python中的实现，并进一步探讨优先队列的工作原理、实际应用以及与其他数据结构的结合。此外，我们还将深入学习堆的高级技巧，包括扩展的堆结构和性能分析，并最终通过实践演练来巩固和深化理解。让我们开始探索堆与优先队列的奥妙吧！

# 2. 理解堆结构及其在Python中的应用

堆结构是一种特殊的树形数据结构，它具有许多重要的性质和广泛的应用。在本章节中，我们将深入探讨堆的基本概念和性质，并详细介绍如何在Python中实现堆结构。我们会从堆的基本操作开始，然后深入到Python标准库heapq模块的使用，最后通过构建自定义堆类来加深对堆操作的理解。

## 2.1 堆的基本概念和性质

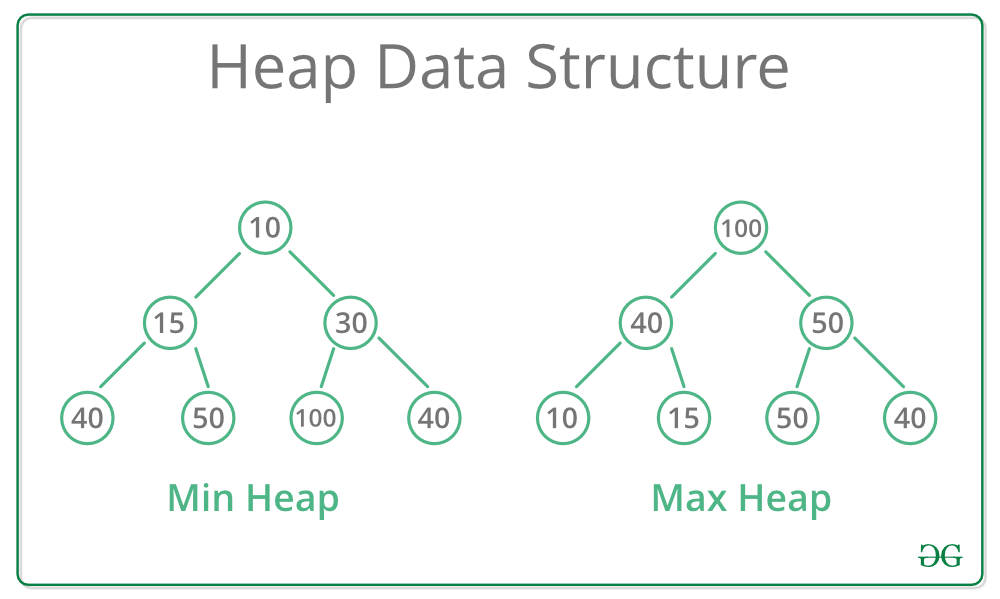
堆是一种完全二叉树，它满足堆性质：任何一个父节点的值都必须大于或等于（在最小堆中）或小于或等于（在最大堆中）其子节点的值。堆结构通常用于实现优先队列，在许多算法和应用中都扮演着重要角色。

### 2.1.1 完全二叉树与堆的关系

完全二叉树是一种特殊的二叉树，除了最后一层外，每一层都被完全填满，且最后一层的节点都靠左排列。堆是一种特殊的完全二叉树，其每个节点都满足堆性质。由于完全二叉树的这一特性，堆可以使用数组来高效地表示。

在数组表示中，对于任意位置i的节点，其左子节点的位置为2i+1，右子节点的位置为2i+2，而其父节点的位置为(i-1)/2（结果取整）。这种数组表示方法为堆操作提供了良好的空间和时间效率。

### 2.1.2 堆的操作：插入与删除

堆支持两种基本操作：插入（insert）和删除（delete）。在插入操作中，新元素会被添加到堆的末尾，然后通过上浮（或称“堆化”）过程调整堆以保持堆性质。删除操作通常是指删除堆顶元素（最大或最小元素），然后将最后一个元素移动到堆顶，之后通过下沉（或称“堆化”）过程来调整堆。

上浮和下沉操作的时间复杂度均为O(log n)，其中n是堆中元素的数量。这是因为在树形结构中，从一个节点到达树顶或树底的距离最大为树的高度，而完全二叉树的高度为log(n)。

## 2.2 Python标准库中的堆实现

Python标准库提供了heapq模块，它是一个堆队列算法的实现，也就是优先队列算法。该模块提供了对堆的操作，使得堆的使用变得更加简单和直接。

### 2.2.1 heapq模块概述

heapq模块提供了几个与堆相关的方法，其中包括：

- `heappush(heap, item)`：将item压入堆中。
- `heappop(heap)`：弹出堆中的最小项。
- `heapify(heap)`：将列表转化为一个堆，这个操作的时间复杂度为O(n)。
- `heapreplace(heap, item)`：弹出并返回堆中最小的项，并将新的item压入堆中。

这些方法都可以在O(log n)的时间复杂度内完成操作。

### 2.2.2 构建和使用最小堆

最小堆是堆结构中的一种，它保证了堆顶元素是所有元素中最小的。在Python中使用最小堆非常简单，只需导入heapq模块并利用其提供的函数即可。

import heapq

# 创建一个空堆
min_heap = []

# 向堆中添加元素
for num in [5, 3, 1, 8, 2, 9, 4, 7]:
    heapq.heappush(min_heap, num)

# 弹出堆中最小的元素
while min_heap:
    print(heapq.heappop(min_heap))

# 输出结果将是：1, 2, 3, 4, 5, 7, 8, 9

### 2.2.3 构建和使用最大堆

最大堆与最小堆类似，但它维护的是最大的元素在堆顶。Python标准库中并没有直接提供最大堆的实现，但我们可以通过一种小技巧来使用heapq模块构建最大堆。

import heapq

def push_max_heap(heap, item):
    # 由于heapq是最小堆实现，所以将元素取负后使用heappush
    heapq.heappush(heap, -item)

def pop_max_heap(heap):
    # 弹出最小元素（因为元素取了负，所以是最小），再取负得到最大元素
    return -heapq.heappop(heap)

max_heap = []
for num in [5, 3, 1, 8, 2, 9, 4, 7]:
    push_max_heap(max_heap, num)

while max_heap:
    print(pop_max_heap(max_heap))

# 输出结果将是：9, 8, 7, 5, 4, 3, 2, 1

## 2.3 自定义堆类实现

虽然Python的标准库提供了heapq模块来实现堆的功能，但自定义堆类可以让我们对堆的内部实现有更深入的理解。自定义堆类还可以增加额外的功能和更复杂的操作。

### 2.3.1 堆的数组表示法

堆通常使用数组来表示，这是因为数组表示法可以有效地利用数组索引的计算规则来访问父节点和子节点。数组表示法对于理解和实现堆操作是非常直观的。

### 2.3.2 插入和删除操作的详细实现

在自定义堆类中，我们需要实现几个关键的方法：`insert`用于添加元素，`delete`用于删除堆顶元素，并进行必要的堆调整。这两个方法在逻辑上需要实现上浮和下沉过程。

class MinHeap:
    def __init__(self):
        self.heap = []

    def _parent(self, i):
        return (i - 1) // 2

    def _left_child(self, i):
        return 2 * i + 1

    def _right_child(self, i):
        return 2 * i + 2

    def _swap(self, i, j):
        self.heap[i], self.heap[j] = self.heap[j], self.heap[i]

    def insert(self, item):
        self.heap.append(item)
        self._bubble_up(len(self.heap) - 1)

    def _bubble_up(self, i):
        while i != 0 and self.heap[self._parent(i)] > self.heap[i]:
            self._swap(i, self._parent(i))
            i = self._parent(i)

    def delete(self):
        if len(self.heap) == 0:
            return None
        if len(self.heap) == 1: