功率谱与信号处理：揭示功率谱在信号处理中的关键作用

# 1. 功率谱的概念与理论基础

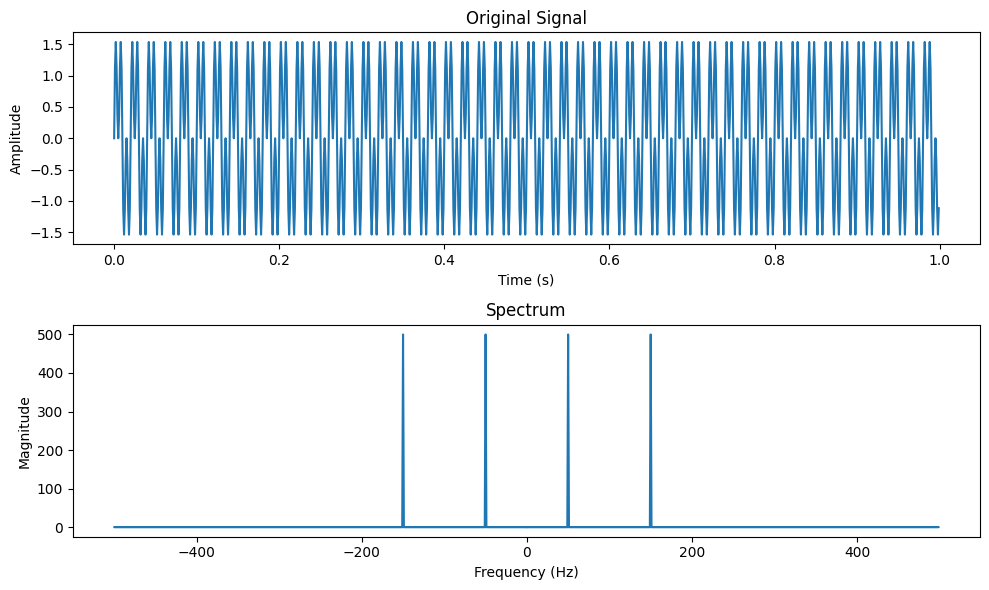
功率谱是信号处理中用于分析信号功率分布在频率域上的工具。它描述了信号中不同频率分量的功率，为理解信号的特性和提取有用信息提供了重要依据。

功率谱的理论基础源于傅里叶变换，它将时域信号分解为一系列正弦波分量。每个分量的幅度和相位对应于信号在特定频率上的功率和相位信息。通过计算信号的功率谱，我们可以获得信号在不同频率上的能量分布，从而深入了解信号的频域特性。

# 2. 功率谱的计算与分析

### 2.1 时域与频域的相互转换

#### 2.1.1 傅里叶变换

傅里叶变换是一种将时域信号转换为频域信号的数学工具。它将一个时域函数分解成一系列正弦波和余弦波的叠加，每个波都有特定的频率和幅度。

**傅里叶变换公式：**

X(f) = ∫_{-\infty}^{\infty} x(t) e^(-2πift) dt

其中：

* `X(f)` 是频域信号
* `x(t)` 是时域信号
* `f` 是频率

**代码逻辑分析：**

傅里叶变换通过对时域信号进行积分，将时域中连续的信号分解为频域中一系列离散的频率分量。积分过程将时域信号与正弦波和余弦波进行逐点乘积，并对所有时间点求和。

#### 2.1.2 离散傅里叶变换

离散傅里叶变换 (DFT) 是傅里叶变换在离散时间信号上的应用。它将一个有限长度的时域信号转换为一个有限长度的频域信号。

**DFT 公式：**

X[k] = ∑_{n=0}^{N-1} x[n] e^(-2πikn/N)

其中：

* `X[k]` 是频域信号的第 `k` 个分量
* `x[n]` 是时域信号的第 `n` 个分量
* `N` 是信号长度

**代码逻辑分析：**

DFT 通过对时域信号进行有限求和，将时域信号分解为频域中一系列离散的频率分量。求和过程将时域信号与正弦波和余弦波进行逐点乘积，并对所有时间点求和。

### 2.2 功率谱的定义与性质

#### 2.2.1 功率谱密度的概念

功率谱密度 (PSD) 是功率谱的一种表示形式，它描述了信号功率在频率上的分布。PSD 定义为信号功率除以频率间隔。

**PSD 公式：**

P(f) = |X(f)|^2 / df

其中：

* `P(f)` 是 PSD
* `X(f)` 是频域信号
* `df` 是频率间隔

**参数说明：**

* `df` 是频率间隔，通常取为 1。

#### 2.2.2 功率谱的统计性质

功率谱具有以下统计性质：

* **非负性：** PSD 始终为非负值。
* **面积：** PSD 的积分等于信号的总功率。
* **对称性：**对于实值信号，PSD 关于零频率对称。

# 3.1 信号增强与降噪

功率谱在信号处理中的一项重要应用是信号增强与降噪。通过分析信号的功率谱，我们可以识别和去除噪声成分，从而提高信号的信噪比（SNR）。

#### 3.1.1 滤波器的设计与实现

滤波器是用于处理信号的设备或算法，其作用是根据信号的频率特性选择性地通过或衰减信号。在信号增强与降噪中，滤波器可以用来去除特定频率范围内的噪声。

**代码块：**

import numpy as np
import scipy.signal as sig

# 生成正弦信号
t = np.linspace(0, 1, 1000)
f = 100  # 信号频率
x = np.sin(2 * np.pi * f * t)

# 添加噪声
noise = np.random.randn(len(x))
y = x + noise

# 设计带通滤波器
order = 4  # 滤波器阶数
cutoff_low = 90  # 低截止频率
cutoff_high = 110  # 高截止频率
b, a = sig.butter(order, [cutoff_low, cutoff_high], btype='bandpass')

# 滤波信号
y_filtered = sig.filtfilt(b, a, y)

**逻辑分析：**

* `scipy.signal.butter()` 函数用于设计带通滤波器。
* `order` 参数指定滤波器的阶数，表示滤波器的极点和零点的数量。
* `cutoff_low` 和 `cutoff_high` 参数指定滤波器的截止频率，表示滤波器通过和衰减信号的频率范围。
* `sig.filtfilt()` 函数用于对信号进行滤波，`b` 和 `a` 分别表示滤波器的分子和分母系数。

#### 3.1.2 噪声的抑制与消除

除了使用滤波器之外，还可以通过其他方法来抑制和消除噪声。

**自适应滤波器：** 自适应滤波器可以根据输入信号的统计