【公钥加密算法深度解析】：RSA, DSA, ECC在Crypto.PublicKey的实现

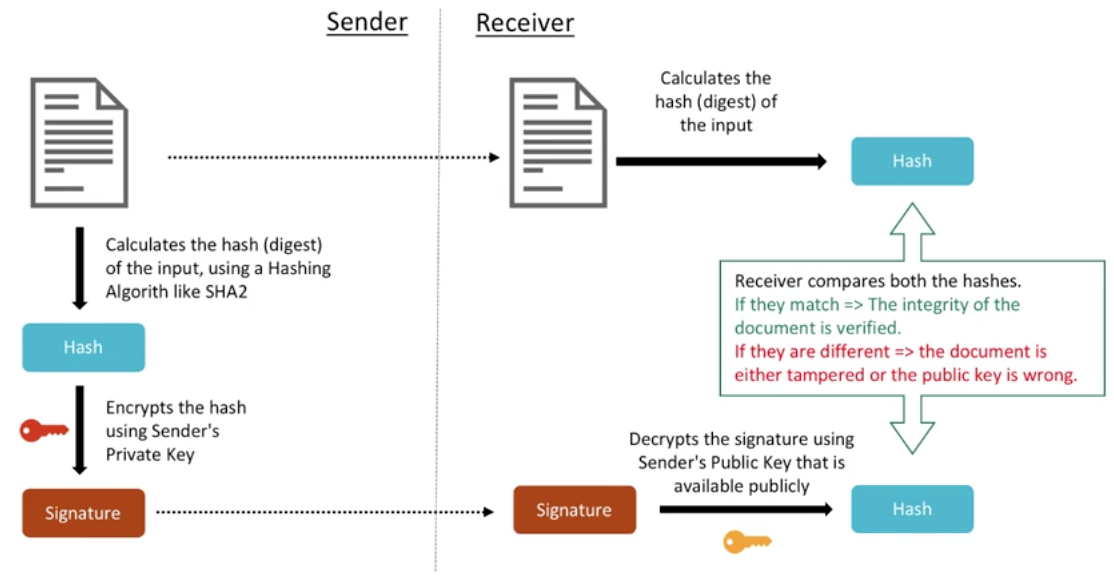
# 1. 公钥加密算法概述

公钥加密算法是现代信息安全的基石，它依赖于数学上的难题来保证通信的安全性。与对称密钥算法相比，公钥算法的密钥分发问题得到了解决，因为每个用户都有一个密钥对：公钥和私钥。公钥可以公开分享，用于加密信息，而私钥必须保密，用于解密接收到的信息。这种机制不仅简化了密钥管理，还提供了数字签名功能，增强了数据的完整性和身份验证。

公钥算法中最著名的例子包括RSA、DSA和ECC等。RSA基于大整数的分解难题，而DSA依赖于离散对数问题。ECC则利用椭圆曲线上的离散对数问题，提供了一种效率更高的加密方式。这些算法在不同的安全需求和性能要求下有不同的应用场景。

本章将概述公钥加密算法的基本概念，并为后续章节中对RSA、DSA和ECC算法的深入探讨奠定基础。我们将介绍这些算法的理论基础、加密解密原理以及如何在Python中实现它们。通过对比不同算法的性能，我们将帮助读者选择最合适的公钥加密算法来满足特定的应用需求。

# 2. RSA算法的理论与实践

RSA算法作为公钥加密领域的经典代表，其理论基础和实践应用一直是信息安全领域的研究热点。本章节将深入探讨RSA算法的数学原理、加密解密机制以及如何在Python中实现RSA算法。

## 2.1 RSA算法的数学基础

### 2.1.1 大整数分解问题

RSA算法的核心是基于大整数分解的困难性。在数学上，大整数分解指的是将一个合数分解成两个或多个素数的过程。对于小整数来说，分解是容易的，但随着整数位数的增加，分解所需的时间呈指数级增长。这一特性是RSA算法安全性的基础。

### 2.1.2 欧拉函数与欧拉定理

RSA算法使用欧拉函数φ(n)来计算模n的乘法群的阶，其中n是两个素数p和q的乘积。欧拉定理指出，对于与n互质的整数a，有a^φ(n) ≡ 1 (mod n)。RSA算法利用这一性质来确定公钥和私钥。

## 2.2 RSA算法的加密解密原理

### 2.2.1 密钥生成过程

RSA密钥对的生成过程包括选择两个大素数p和q，计算n = p*q以及φ(n)，然后选择一个小于φ(n)的整数e，使得e和φ(n)互质。私钥d是e的模φ(n)乘法逆元。

### 2.2.2 加密和解密过程

加密过程使用公钥(n, e)对明文M进行加密，得到密文C，公式为C ≡ M^e (mod n)。解密过程使用私钥(n, d)对密文C进行解密，得到明文M，公式为M ≡ C^d (mod n)。由于e*d ≡ 1 (mod φ(n))，因此这个过程是可逆的。

## 2.3 RSA算法在Python中的实现

### 2.3.1 Crypto.PublicKey.RSA模块介绍

在Python中，可以使用`pycrypto`库中的`Crypto.PublicKey.RSA`模块来实现RSA算法。该模块提供了生成密钥、加密和解密等功能。

### 2.3.2 实例：RSA密钥对的生成与使用

以下是一个使用`Crypto.PublicKey.RSA`模块生成RSA密钥对和使用密钥对加密解密的实例：

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
import binascii

# 生成RSA密钥对
key = RSA.generate(2048)

# 获取公钥和私钥
public_key = key.publickey()
private_key = key

# 明文消息
message = "Hello, RSA!"

# 使用公钥加密
encryptor = PKCS1_OAEP.new(public_key)
cipher_text = encryptor.encrypt(message.encode())
print(f"Encrypted Message: {binascii.hexlify(cipher_text).decode()}")

# 使用私钥解密
decryptor = PKCS1_OAEP.new(private_key)
plain_text = decryptor.decrypt(cipher_text)
print(f"Decrypted Message: {plain_text.decode()}")

### 代码逻辑解读分析

1. **密钥生成**：`RSA.generate(2048)`生成了一个2048位的RSA密钥对。
2. **公钥获取**：`public_key = key.publickey()`获取公钥。
3. **私钥获取**：直接使用`private_key = key`获取私钥。
4. **消息加密**：使用`PKCS1_OAEP.new(public_key)`创建一个加密器对象，然后调用`encrypt()`方法对消息进行加密。
5. **消息解密**：使用`PKCS1_OAEP.new(private_key)`创建一个解密器对象，然后调用`decrypt()`方法对密文进行解密。

### 参数说明

- `2048`：密钥长度，表示使用了2048位的RSA算法。
- `PKCS1_OAEP`：使用的加密/解密填充方案，OAEP是一种带有优化的填充方案。

通过本章节的介绍，我们了解了RSA算法的数学基础、加密解密原理以及在Python中的实现方法。RSA算法的应用非常广泛，包括但不限于安全通信、数字签名和身份验证等。下一章节我们将探讨另一种公钥算法——DSA算法的理论与实践。

# 3. DSA算法的理论与实践

数字签名算法（DSA）是一种用于验证数字信息完整性和来源的公钥加密算法。它基于离散对数问题，被广泛用于数据的完整性验证和身份认证。在本章节中，我们将深入探讨