【降维技术精讲】：PCA与t-SNE在Python中的深入实现

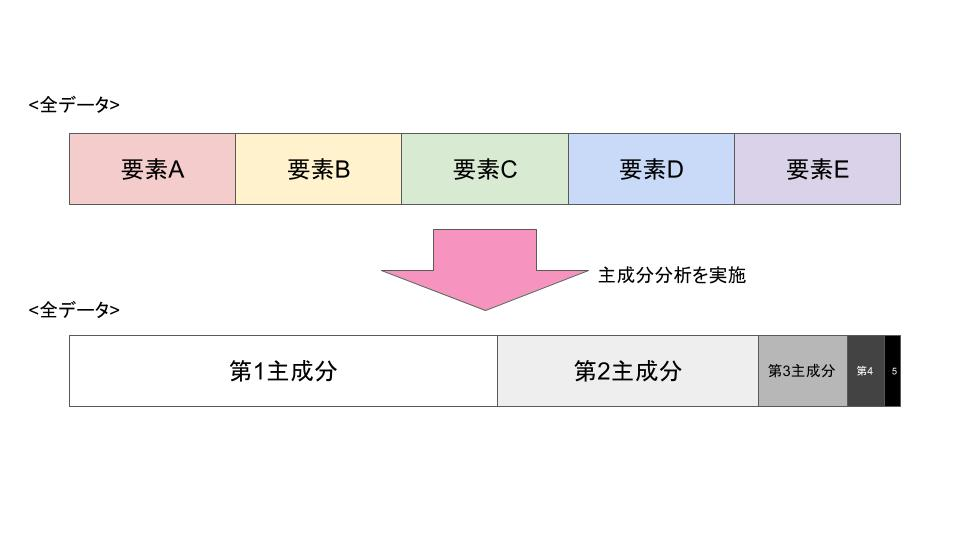
# 1. 降维技术概述及应用场景

降维技术是机器学习和数据挖掘领域中不可或缺的一部分。它们旨在简化数据结构，同时保留原始数据的关键特征。降维可以分为两大类：线性降维和非线性降维。线性降维方法如主成分分析（PCA）通过投影将高维数据转换到较低维的空间中，而非线性降维技术如t分布随机邻域嵌入（t-SNE）则尝试保留原始数据的结构特性。

在本章中，我们将首先探讨降维技术的通用概念，包括其重要性、分类和常用技术。接下来，我们将重点介绍这些技术在不同领域的应用场景，如在生物信息学中的基因表达数据分析，在计算机视觉中的图像压缩，在商业智能中的消费者行为模式识别等。通过这些案例，我们将揭示降维技术如何在实际问题中实现数据的可视化、特征提取和噪音过滤，以及如何为后续的分析和学习提供更好的数据基础。

# 2. 主成分分析（PCA）的理论与实践

## 2.1 PCA的数学原理

### 2.1.1 数据集的预处理和标准化

在开始PCA之前，预处理和标准化数据是至关重要的步骤。原始数据往往包含噪声和不同尺度的特征，直接进行PCA可能会导致结果偏向于具有较大方差的特征，从而失去准确性。标准化的目的就是让所有特征对于PCA算法有相同的权重，使得算法可以公平地处理每个特征。

以下是标准化的步骤和对应的Python代码示例：

import numpy as np

# 假设我们有一个数据集X
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

# 对数据集进行标准化处理
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

print(X_scaled)

在上述代码中，我们首先导入了`numpy`库用于数据操作，然后创建了一个简单的数据集`X`。接下来，我们使用`sklearn.preprocessing.StandardScaler`类对数据进行标准化。标准化处理确保了每个特征的均值为0，方差为1，这样在应用PCA时，每个特征都能公平地参与到主成分的计算中。

### 2.1.2 协方差矩阵及其特征分解

经过预处理和标准化的数据集，接下来需要计算其协方差矩阵。协方差矩阵是一个描述数据集中各个变量之间线性相关性强度和方向的矩阵。其计算公式为：

\Sigma = \frac{1}{n-1}X^TX

其中，$\Sigma$为协方差矩阵，$X$为标准化后的数据矩阵，$n$为样本数。

协方差矩阵确定了，我们便可以找到其特征值和特征向量，特征值代表了数据在这个方向上的方差大小，而对应的特征向量则指示了数据在特征空间的分布方向。

代码实现和逻辑解释如下：

# 计算协方差矩阵
cov_matrix = np.cov(X_scaled.T)

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

# 输出特征值和特征向量
print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)

在该代码块中，我们首先使用`numpy`的`cov`函数计算标准化数据的协方差矩阵。然后，通过`linalg.eig`函数来找到协方差矩阵的特征值和特征向量。计算出的特征向量将用于数据的投影，特征值则用于衡量每个主成分的重要性。

## 2.2 PCA在Python中的实现

### 2.2.1 使用scikit-learn实现PCA

scikit-learn库提供了一个非常方便的接口来实现PCA，只需要几行代码，就可以完成从数据预处理到主成分提取的整个过程。以下是使用scikit-learn实现PCA的基本步骤：

from sklearn.decomposition import PCA

# 创建PCA对象，设置要保留的主成分数量
pca = PCA(n_components=2)

# 对数据集X进行PCA降维
X_pca = pca.fit_transform(X_scaled)

print("PCA降维后的数据:", X_pca)

在这个代码块中，我们首先导入了`PCA`类，然后创建了一个`PCA`对象，指定了我们想要保留的主成分数量为2。之后，我们使用`fit_transform`方法，将标准化后的数据`X_scaled`进行降维处理，得到降维后的数据`X_pca`。

### 2.2.2 PCA参数调优和结果解释

在PCA的应用中，选择合适的主成分数量是一个重要的决策。我们可以通过分析特征值的大小来决定要保留多少主成分。通常，保留的主成分应当累计解释大部分的数据方差。

下面是使用累积解释方差来决定主成分数量的代码：

# 计算累计解释方差比率
cumulative_variance = np.cumsum(eigenvalues) / np.sum(eigenvalues)

# 输出累计解释方差比率
print("累计解释方差比率:", cumulative_variance)

# 绘制累计解释方差比率图
import matplotlib.pyplot as plt

plt.plot(cumulative_variance)
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Explained Variance by Different Principal Components')
plt.show()

在上述代码中，我们使用了之前计算得到的特征值数组`eigenvalues`，计算了各个主成分对总体方差的贡献，并绘制了一个图表，直观显示了不同主成分解释的累计方差。通过这张图，我们可以直观地选择一个阈值，例如选择解释了85%以上方差的主成分数量。

## 2.3 PCA的实际应用案例

### 2.3.1 高维数据的可视化

PCA的一个重要应用是高维数据的可视化。对于具有大量特征的数据集，我们可以使用PCA将数据投影到2维或3维空间中，以便于观察和分析数据的结构和分布。

以下是使用PCA进行数据可视化的一个例子：

import matplotlib.pyplot as plt

# 使用PCA将数据降维到2维空间
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 绘制降维后的数据散点图
plt.scatter(X_pca[:, 0], X_pca[:, 1])
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('2D Visualization of PCA-Reduced Data')
plt.show()

在该代码块中，我们首先执行PCA降维操作，将原始数据集`X_scaled`投影到两个主成分组成的2维空间中。然后，我们使用`matplotlib`库绘制了一个散点图，该图展示了降维后的数据点的分布情况。通过这样的可视化，我们能够快速洞察数据的聚类特性和潜在的结构。

### 2.3.2 提升机器学习模型性能的实例

PCA另一个应用是在预处理阶段帮助提升机器学习模型的性能。通过移除冗余特征和噪声，PCA可以改善模型的训练效率，同时减少过拟合的风险。

举一个简单的例子，假设我们有一个分类