维度缩减技术：PCA与t-SNE在Python中的权威实现

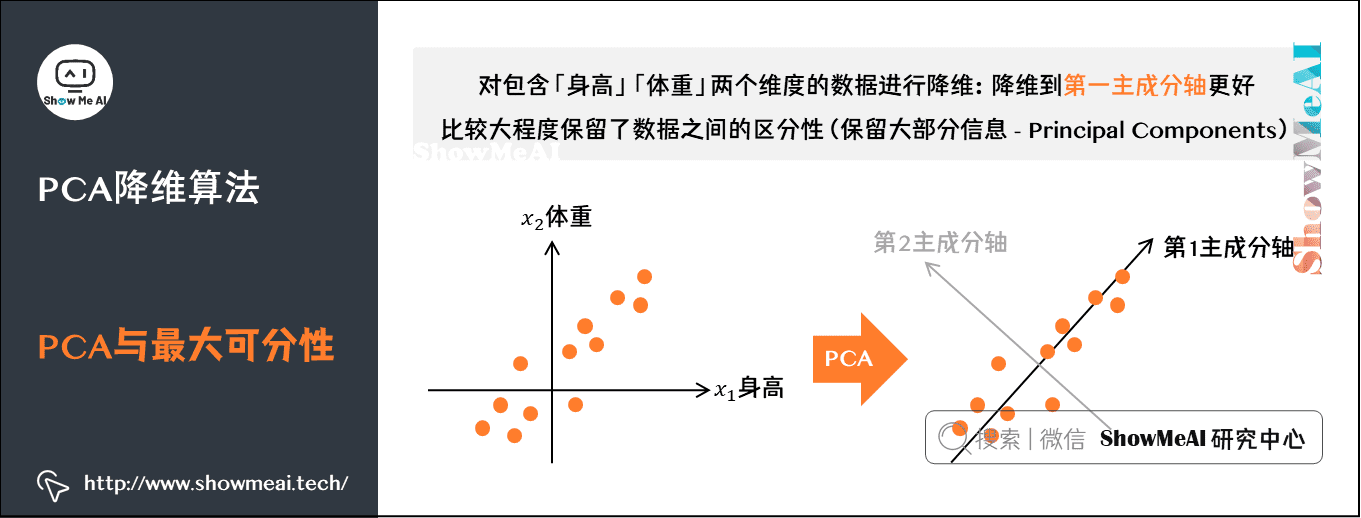
# 1. 维度缩减技术概述

## 1.1 维度缩减技术简介
在处理高维数据时，维度缩减技术作为数据预处理的关键步骤，旨在降低数据集的复杂性，同时尽量保留数据的重要信息。通过减少变量的数目，可以显著提升数据处理的效率，以及提高许多机器学习算法的性能。

## 1.2 维度缩减的挑战与机遇
随着数据量的激增，如何有效地进行维度缩减成为了一个挑战。虽然降维可以带来好处，例如减少计算资源的需求，但过度缩减可能会导致信息的丢失，影响最终的分析结果。因此，合理选择降维技术对于分析高维数据至关重要。

## 1.3 降维技术的应用场景
降维技术广泛应用于生物信息学、图像处理、自然语言处理等领域。在这些场景中，高维数据处理和分析是不可或缺的一部分，降维不仅可以提高模型的准确性，还可以提升数据可视化的效果。

在下一章中，我们将深入探讨主成分分析（PCA）——一种广泛使用的线性降维技术，并通过理论和实践案例，展示其在数据分析中的作用。

# 2. 主成分分析（PCA）理论与实践

## 2.1 PCA的基本概念和数学原理

### 2.1.1 维度缩减的必要性

在数据科学领域，维度缩减是将数据集从高维空间转换到低维空间的过程，以便于可视化、提高计算效率或增强模型性能。当数据的特征维数很高时，会引发所谓的“维度诅咒”，即模型的性能会下降，计算成本则会大幅上升。维度缩减不仅简化了数据结构，还能减少噪声和冗余特征带来的干扰，提高分析的准确性和效率。

### 2.1.2 PCA的数学模型和步骤

主成分分析（PCA）是一种广泛使用的无监督线性降维技术。PCA通过正交变换将可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。其数学模型依赖于特征值分解或奇异值分解（SVD）的概念。实现PCA的基本步骤包括：

1. 数据标准化：确保每个特征具有零均值和单位方差。
2. 协方差矩阵计算：描述了数据特征之间的相互关系。
3. 特征值和特征向量计算：特征值表示方差大小，特征向量指示数据分布的方向。
4. 选择主成分：基于特征值的大小选择主成分，并重新排序以保留最多的信息。
5. 数据投影：将原始数据集投影到选定的主成分上以完成降维。

## 2.2 在Python中实现PCA

### 2.2.1 使用scikit-learn库进行PCA

在Python中，`scikit-learn`库是实现PCA的一个常用工具。以下是使用`scikit-learn`进行PCA的一个基本示例代码：

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import numpy as np

# 示例数据集
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 创建PCA对象，指定降维后的维数为1
pca = PCA(n_components=1)

# 对数据集进行PCA处理
X_pca = pca.fit_transform(X_scaled)

# 输出降维后的结果
print(X_pca)

在这个例子中，首先导入必要的库，然后创建了一个示例数据集，并通过`StandardScaler`进行数据标准化。接着，创建了一个`PCA`实例，指定了要降维到的维数，最后通过`fit_transform`方法将数据集降维，并打印结果。

### 2.2.2 PCA的参数选择和调优

`scikit-learn`中的PCA类提供了多个参数来控制降维的过程。一些常见的参数包括：

- `n_components`: 指定降维后的维数或主成分的数量。
- `whiten`: 是否将数据白化（调整特征值使它们相等）。
- `svd_solver`: 用于计算SVD的方法，可选值包括`'auto'`、`'full'`、`'arpack'`和`'randomized'`。

调优PCA通常涉及到选择合适的主成分数量，这可以通过累计解释方差的比例来决定。以下是一个根据累计解释方差决定主成分数量的示例：

pca = PCA().fit(X_scaled)
cumulative_variance = np.cumsum(pca.explained_variance_ratio_)

# 输出累计解释方差
print(cumulative_variance)

# 选择累积解释方差达到95%的主成分数量
n_components = np.argmax(cumulative_variance >= 0.95) + 1
print(f"Number of components to retain: {n_components}")

### 2.2.3 PCA结果的解读和应用

解读PCA结果对于理解数据降维后的分布至关重要。解释主成分通常需要考虑它们的特征值和特征向量。特征值越大，对应的主成分解释数据的方差就越多。特征向量则提供了原始特征在新主成分中的权重。

在实际应用中，降维后的数据可用于多种目的，包括可视化、特征提取和数据压缩等。例如，可以将降维后的数据用于监督学习模型的训练，以提高模型的效率和性能。

## 2.3 PCA案例分析

### 2.3.1 面向数据集的PCA应用

让我们以一个具体的数据集为例，来演示如何将PCA应用于特征降维。假设有一个包含多个特征的人口统计信息数据集，我们想要减少特征的维数以便于分析和可视化。

import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 加载数据集
data = pd.read_csv('demographics.csv')

# 选择部分特征
X = data[['age', 'income', 'education', 'marital_status']]

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 创建并应用PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 将结果转换为DataFrame，方便后续操作
df_pca = pd.DataFrame(data=X_pca, columns=['principal component 1', 'principal component 2'])

# 将原始特征添加到结果中，以便于解释PCA结果
df_pca = pd.concat([df_pca, data[['age', 'income', 'education', 'marital_status']]], axis=1)

# 输出降维后的数据集
print(df_pca)

### 2.3.2 PCA在特征提取中的作用

PCA常用于机器学习中的特征提取，尤其是在处理图像或音频数据时，PCA可以帮助我们从高维数据中提取最重要的特征，简化模型，减少过拟合的风险。以下是一个如何在图像处理中使用PCA进行特征提取的示例：

from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
import matplotlib.pyplot as