数据挖掘中的维度缩减：简化复杂数据集的5大方法，让你轻松应对！

# 1. 数据挖掘与维度缩减的概述

在当前信息技术飞速发展的时代，数据挖掘已成为分析和理解大量数据的有力工具。数据挖掘涉及从海量数据集中提取有用信息和知识的过程，而维度缩减是这一过程中的关键环节。它致力于降低数据的复杂性，同时尽可能保留数据中重要的特征信息。维度缩减不仅有助于提高数据处理效率，还能增强机器学习模型的性能和可解释性。简而言之，维度缩减帮助我们在保留数据核心价值的前提下，处理高维数据集带来的挑战。在本章中，我们将介绍维度缩减的基本概念，高维数据带来的挑战，以及如何通过数据挖掘技术应对这些挑战，为后续章节打下坚实的基础。

# 2. 维度缩减的重要性与方法论

### 维度缩减的定义与目的

#### 维度缩减的基本概念

在现代数据分析中，维度缩减是一种关键的技术，用于减少数据集中的特征数量，同时尽可能保留数据的重要信息。高维数据集通常包含大量特征，这些特征可能会引入噪声和复杂性，导致模型难以训练，过拟合的风险增加，并且影响模型的可解释性。通过减少这些特征的数量，维度缩减有助于简化模型，提高计算效率，增强模型的泛化能力，并可能揭示数据中隐藏的结构。

#### 高维数据的挑战

在高维数据集中，一个突出的问题是“维度的诅咒”（Curse of Dimensionality），它描述了随着特征数量的增加，数据稀疏性增加，使得数据点之间的距离变得不那么有意义。这种情况给数据处理和分析带来了许多挑战：

1. **数据稀疏性：** 高维空间中的数据点通常稀疏分布，导致很难确定点之间的距离是否真正反映了数据的相似性。
2. **计算资源：** 高维数据集需要更多的计算资源进行处理，包括存储空间、处理时间和内存使用量。
3. **过拟合风险：** 模型可能会学习到数据中的随机噪声而非实际的信号，导致模型在未见过的数据上表现不佳。
4. **可视化困难：** 在高维空间中，传统的数据可视化方法变得不再有效，难以直观理解数据的分布和关系。

### 维度缩减的理论框架

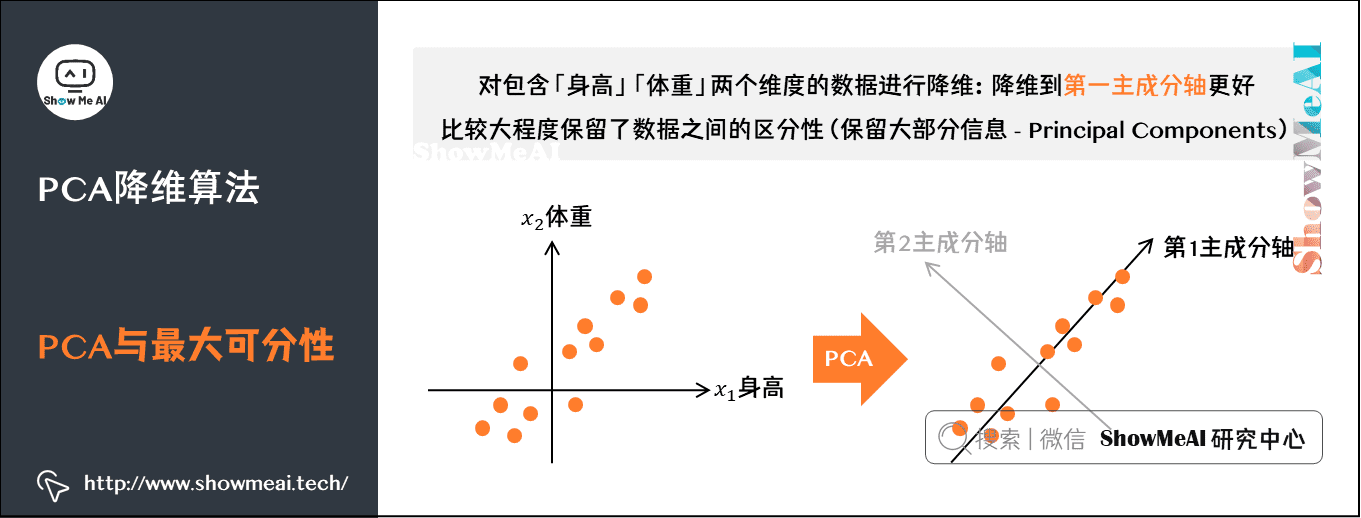
#### 主成分分析（PCA）的数学基础

主成分分析（PCA）是一种常用的统计方法，它通过正交变换将一组可能相关的变量转换成一组线性不相关的变量，称为主成分。PCA的核心在于找出数据中方差最大的方向，并在这些方向上投影数据，从而实现降维。

PCA的数学基础可以概括为以下步骤：

1. **数据标准化：** 将数据按特征进行中心化处理，使得每个特征的均值为零。
2. **协方差矩阵计算：** 通过计算标准化数据的协方差矩阵，来捕捉特征之间的线性关系。
3. **特征分解：** 对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. **选择主成分：** 根据特征值的大小选择最重要的特征向量，作为主成分。
5. **数据降维：** 将原始数据投影到选出的主成分上，得到降维后的数据。

#### 常用的维度缩减算法概览

维度缩减是一个广泛的研究领域，除了PCA之外，还有其他多种算法可以用于降维，每种算法都有其特定的应用场景和优势：

1. **线性判别分析（LDA）：** 用于分类问题的降维方法，尝试最大化类间距离，最小化类内距离。
2. **t-分布随机邻域嵌入（t-SNE）：** 一种非线性降维技术，特别适用于高维数据的可视化。
3. **等度映射（Isomap）：** 尝试保持原始数据的几何结构，在保持局部邻域关系的同时进行全局降维。
4. **局部线性嵌入（LLE）：** 寻找一个全局低维嵌入，同时保持每个数据点的局部线性关系。

### 应用维度缩减的潜在风险

#### 信息损失的问题

维度缩减的一个主要担忧是信息的损失。在减少特征数量的同时，可能丢弃了数据中一些重要信息，这在某些应用场景中可能会导致问题。例如，在医学诊断中，丢弃某些关键的生物指标可能导致诊断准确性的下降。为了平衡降维的益处和潜在的信息损失，选择合适的降维技术和仔细调参是至关重要的。

#### 模型解释性的下降

随着维度缩减，模型的解释性可能会降低。例如，PCA降维后得到的主成分是原始特征的线性组合，这些组合可能难以用业务术语来解释。在某些行业，如金融和医疗，模型的可解释性是一个重要的需求。因此，降维操作需要谨慎进行，以确保关键信息没有丢失，并且模型仍然能够提供有意义的洞察。

在应用维度缩减时，理解和评估这些风险对于确保最终模型的成功至关重要。维度缩减方法应根据具体的数据特性和业务需求来选择，并在实施过程中进行细致的调优和验证。接下来的章节将深入探讨主成分分析（PCA）的具体实践操作和应用案例。

# 3. 实践操作：主成分分析（PCA）

## 3.1 PCA的计算步骤详解

### 3.1.1 数据标准化

在进行主成分分析之前，数据的标准化处理是一个关键步骤。数据标准化的目的是为了消除不同量纲或者数量级对分析结果的影响。在数据科学中，常用的方法是减去均值并除以标准差，这个过程也被称为z-score标准化。

具体来说，对于一个数据集中的每个变量 \(X_i\)，标准化的计算公式如下：

\[ z_{ij} = \frac{(x_{ij} - \mu_i)}{\sigma_i} \]

这里 \(x_{ij}\) 表示第 \(i\) 个变量的第 \(j\) 个观测值，\(\mu_i\) 是该变量的均值，而 \(\sigma_i\) 是该变量的标准差。

使用Python中的pandas库可以方便地进行数据的标准化处理。下面是一个简单的代码示例：

import pandas as pd
from sklearn.preprocessing import StandardScaler

# 假设dataframe是包含数据的pandas DataFrame
scaler = StandardScaler()
dataframe_scaled = scaler.fit_transform(dataframe)

### 3.1.2 协方差矩阵的构建和特征分解

标准化之后的数据下一步是构建协方差矩阵。协方差矩阵能够反映变量之间的相互关系，对于PCA来说，它是理解数据中变量相关性的关键。

一个 \(p \times p\) 维度的协方差矩阵 \(C\) 的计算公式为：

\[ C = \frac{1}{n-1} X^T X \]

这里 \(X\) 是 \(n \times p\) 的数据矩阵，包含 \(n\) 个观测值和 \(p\) 个特征，\(X^T\) 表示矩阵的转置。

在构建了协方差矩阵之后，接下来进行特征分解，找到协方差矩阵的特征向量和特征值。这些特征向量定义了数据中的主成分方向，而特征值则给出了每个主成分的重要性。

在Python中，使用NumPy库可以完成这个任务：

import numpy as np

# X是已经标准化的特征矩阵
cov_matrix = np.cov(X, rowvar=False)  # 计算协方差矩阵
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)  # 计算特征值和特征向量

### 3.2 PCA的实践应用案例

#### 3.2.1 数据集选择和预处理

在实际操作中，选择合适的数据集并进行预处理是PCA实施的第一步。以著名的鸢尾花（Iris）数据集为例，这是一个包含150个样本和4个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）的数据集。

预处理阶段可能包括检查并处理缺失值、异常值、类别变量编码（如果存在的话），以及前述的数据标准化。

#### 3.2.2 PCA在数据降维中的实际操作

应用PCA进行降维时，需要确定需要保留的主成分数量。通常，这可以通过分析特征值的累积贡献率