机器人避障路径优化：Dijkstra算法与非线性规划

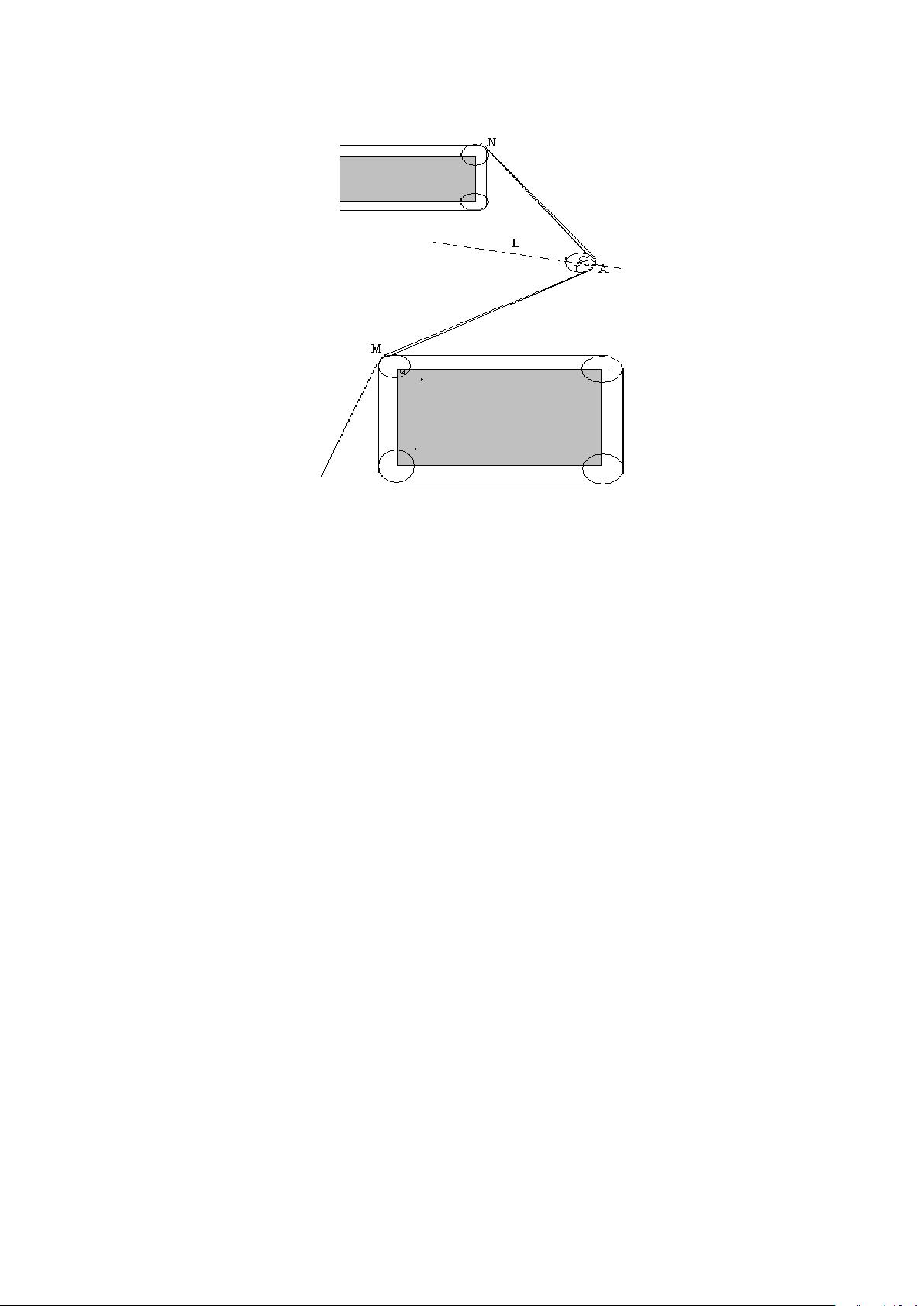
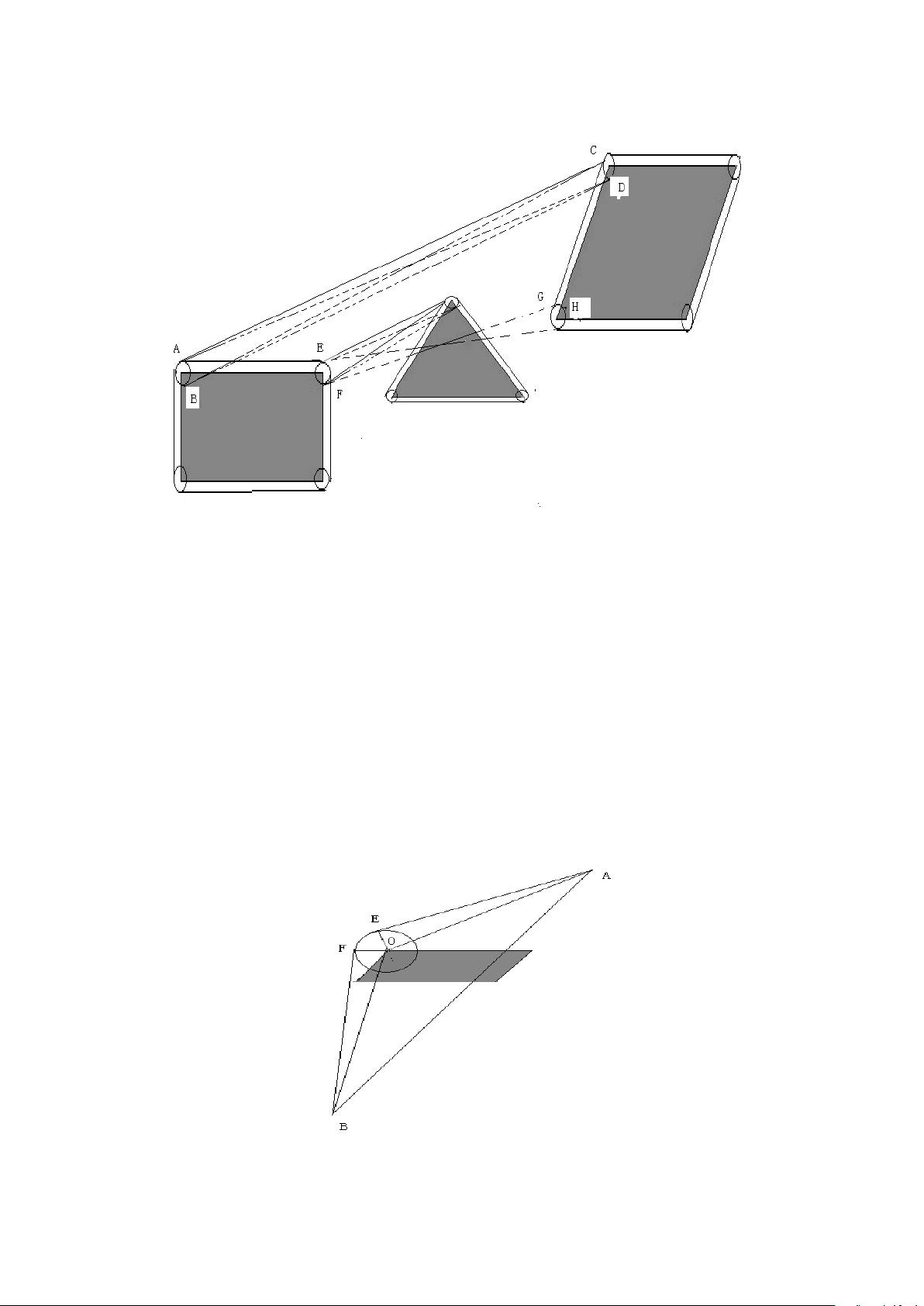
"本文详细探讨了机器人避障问题，主要涉及两个关键问题：最短路径规划和最短时间路径规划。作者运用分析法、图论和非线性规划方法，为解决这些问题提供了深入的理论基础和实用算法。 在最短路径规划部分，作者首先提出了三个基本原理：靠近障碍物顶点转弯的路径最短、转弯圆弧半径最小时路径最短，以及转弯在中间目标点附近的最优位置。基于这些原理，文章通过模型变换和障碍物处理，构建了一个圆角化的障碍图。通过扩充的跨立实验，设计了一种判断切线和圆弧是否在可避障区的算法。接着，应用Dijkstra算法计算出从起点到各个目标点的最短路径，例如O到A、B、C的最短距离分别为471.0372、853.7001和1086.0677个单位。对于需经过中间目标点的路径，采用启发式规则初步计算，再微调得到最短路径，如O-A-B-C-O的路径为2748.699个单位。 在最短时间路径规划方面，文章考虑了路径长度和转弯圆弧半径对时间的影响，构建了以总时间最小为目标的非线性规划模型。借助Matlab编程，求解出从起点到目标点A的最短时间路径为472.4822个单位，最短时间为94.3332秒。这个路径中的圆弧圆心坐标为[pic]，圆弧的两个切点坐标分别是(70.88,212.92)和(77.66,219.87)。 场景图是一个800x800的平面，包含12个不同形状的障碍物，例如编号1的正方形、编号2的圆形、编号3的平行四边形和编号4的三角形等。每个障碍物都有其特定的几何特征，例如边长、半径、顶点坐标等，这些信息用于构建避障模型并进行路径规划。 本文的关键技术包括Dijkstra算法的应用，这是一种用于寻找图中两点间最短路径的经典算法，适合处理带有权重的图。非线性规划模型则允许在考虑多种约束条件下，寻找使目标函数达到极小值的解决方案。此外，跨立实验分析法则是一种实验性的方法，用于验证和优化路径规划策略。 这篇文档详细阐述了如何通过综合运用各种数学工具来解决机器人避障问题，为实际的机器人导航系统设计提供了有价值的理论指导和技术支持。"