探索PCA降维算法的变种：发现更多降维算法

# 1. PCA降维算法的基础**

**1.1 PCA的基本原理**

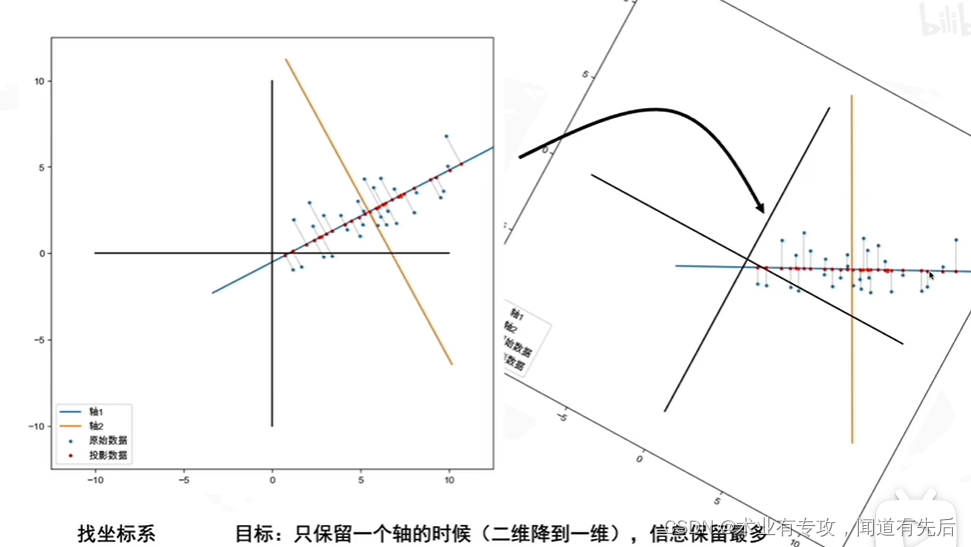
主成分分析（PCA）是一种无监督降维算法，通过线性变换将高维数据投影到低维空间，同时最大化投影数据的方差。PCA的基本原理是寻找数据协方差矩阵的特征向量，并选择前k个特征值对应的特征向量作为降维后的新坐标轴。

**1.2 PCA的优点和缺点**

PCA算法具有以下优点：

- 线性变换，易于理解和实现。
- 计算高效，适合处理大规模数据集。

PCA算法也存在一些缺点：

- 只能处理线性可分的特征。
- 对异常值敏感，容易受到噪声和离群点的影响。

# 2. PCA降维算法的变种

### 2.1 线性判别分析（LDA）

#### 2.1.1 LDA的基本原理

线性判别分析（LDA）是一种监督降维算法，它通过最大化类间方差和最小化类内方差来寻找最优投影方向。具体来说，LDA的目标函数为：

J(W) = \frac{W^T S_b W}{W^T S_w W}

其中：

* `W` 是投影矩阵
* `S_b` 是类间散度矩阵
* `S_w` 是类内散度矩阵

LDA通过求解上述目标函数的特征值和特征向量，得到最优投影方向。

#### 2.1.2 LDA的优点和缺点

**优点：**

* 在类分布呈线性可分的情况下，LDA可以找到最优的投影方向，实现完美的降维。
* LDA具有较好的鲁棒性，对数据中的噪声和异常值不敏感。

**缺点：**

* LDA要求数据满足正态分布，否则降维效果会受到影响。
* LDA对高维数据降维效果不佳，容易出现过拟合。

### 2.2 局部线性嵌入（LLE）

#### 2.2.1 LLE的基本原理

局部线性嵌入（LLE）是一种非线性降维算法，它通过局部重建误差最小化来寻找最优投影方向。具体来说，LLE的算法步骤如下：

1. 对于每个数据点，找到其k个最近邻点。
2. 对于每个数据点，计算其与最近邻点之间的局部重建误差。
3. 寻找一组投影方向，使得所有数据点的局部重建误差之和最小。

#### 2.2.2 LLE的优点和缺点

**优点：**

* LLE是一种非线性降维算法，可以处理非线性数据。
* LLE对数据中的噪声和异常值具有较好的鲁棒性。

**缺点：**

* LLE的计算复杂度较高，不适用于大规模数据集。
* LLE对k值的选择敏感，不同的k值会影响降维效果。

### 2.3 t分布随机邻域嵌入（t-SNE）

#### 2.3.1 t-SNE的基本原理

t分布随机邻域嵌入（t-SNE）是一种非线性降维算法，它通过最小化t分布相似度和高斯相似度之间的差异来寻找最优投影方向。具体来说，t-SNE的算法步骤如下：

1. 计算数据点之间的t分布相似度和高斯相似度。
2. 初始化投影矩阵。
3. 迭代更新投影矩阵，使得t分布相似度和高斯相似度之间的差异最小。

#### 2.3.2 t-SNE的优点和缺点

**优点：**

* t-SNE是一种非线性降维算法，可以处理非线性数据。
* t-SNE能够保留数据中的局部结构和全局结构。

**缺点：**

* t-SNE的计算复杂度很高，不适用于大规模数据集。
* t-SNE对超参数的选择敏感，不同的超参数会影响降维效果。

# 3. PCA降维算法变种的实践应用

### 3.1 人脸识别

**3.1.1 LDA在人脸识别中的应用**

LDA在人脸识别中被广泛用于特征提取和降维。其基本原理是通过最大化类内方差和最小化类间方差，将高维人脸数据投影到低维空间中，同时保持人脸的区分性特征。

**代码块：**

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 加载人脸数据集
X = np.load('face_data.npy')
y = np.load('face_labels.npy')

# 初始化LDA模型
lda = LinearDiscriminantAnalysis(n_components=2)

# 拟合LDA模型
lda.fit(X, y)

# 转换人脸数据
X_lda = lda.transform(X)

**逻辑分析：**

* `LinearDiscriminantAnalysis(n_components=2)`：初始化LDA模型，指定降维后的维度为2。
* `lda.fit(X, y)`：拟合LDA模型，其中X为人脸数据，y为人脸标签。
* `lda.transform(X)`：将人脸数据投影到LDA降维后的空间中，得到降维后的数据X_lda。

**3.1.2 LLE在人脸识别中的应用**

LLE在人脸识别中主要用于非线性降维，它通过局部线性近似的方式，将人脸数据映射到低维空间中，保留人脸的局部结构信息。

**代码块：**

import numpy as n