提升降维效率：PCA降维算法的性能优化

# 1. PCA降维算法概述

PCA（主成分分析）是一种广泛应用于降维的经典算法。其核心思想是将原始数据投影到一个低维空间中，使得投影后的数据尽可能保留原始数据的方差。

PCA算法的优势在于其简单易懂、计算高效，并且在许多实际应用中表现出良好的效果。它可以有效地减少数据的维度，同时最大程度地保留数据的关键信息，从而提高后续处理任务的效率和准确性。

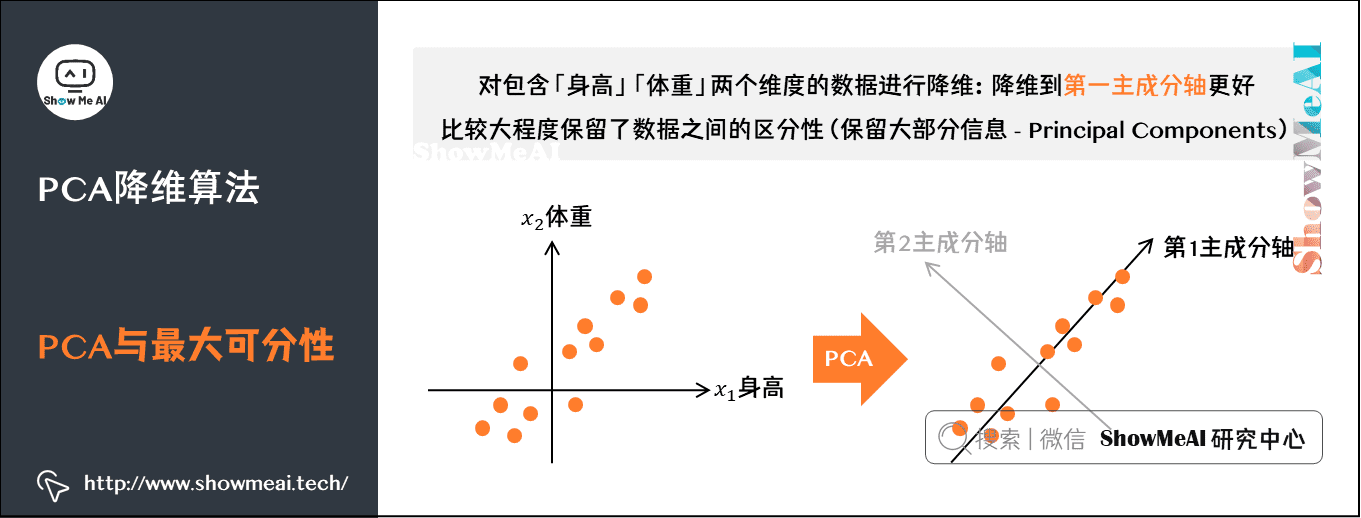
# 2.1 主成分分析（PCA）的原理

主成分分析（PCA）是一种经典的降维算法，它通过线性变换将高维数据投影到低维空间中，同时最大化保留原始数据中的方差。

PCA的基本思想是寻找一组正交基，使得投影到这些基上的数据的方差最大。这些基称为主成分，它们代表了原始数据中最大的变异方向。

### PCA降维的步骤

PCA降维的步骤如下：

1. **数据中心化：**将原始数据减去其均值，使其均值为0。
2. **计算协方差矩阵：**计算原始数据的协方差矩阵，它表示数据中各特征之间的相关性。
3. **特征值分解：**对协方差矩阵进行特征值分解，得到一组特征值和特征向量。
4. **选择主成分：**选择前k个特征值对应的特征向量作为主成分。
5. **投影数据：**将原始数据投影到主成分上，得到降维后的数据。

### PCA降维的数学推导

PCA降维的数学推导如下：

设原始数据为X，其协方差矩阵为C。PCA的目标是找到一个正交变换矩阵P，使得投影后的数据Y = XP满足以下条件：

* Y的方差最大化
* Y的协方差矩阵为对角矩阵

通过求解拉格朗日乘数方程，可以得到P的特征向量就是C的特征向量。而P的特征值表示投影后的数据Y的方差。

因此，PCA降维的数学推导可以总结为：

max ||Y||^2
s.t. Y = XP
      P^T P = I

其中，||Y||^2表示Y的方差，I表示单位矩阵。

# 3.1 PCA降维算法的Python实现

### 导入必要的库

首先，我们需要导入必要的Python库，包括NumPy、Scikit-learn和Matplotlib。

import numpy as np
import sklearn.decomposition as decomp
import matplotlib.pyplot as plt

### 加载数据集

接下来，我们加载一个数据集，该数据集包含我们要降维的数据。

data = np.loadtxt('data.csv', delimiter=',')

### 标准化数据

在应用PCA之前，通常需要对数据进行标准化，以确保所有特征具有相同的尺度。

data_std = (data - np.mean(data, axis=0)) / np.std(data, axis=0)

### 创建PCA模型

现在，我们可以创建一个PCA模型。

pca = decomp.PCA(n_components=2)

### 拟合数据

接下来，我们将PCA模型拟合到标准化后的数据。

pca.fit(data_std)

### 获取主成分

拟合模型后，我们可以获取主成分。

components = pca.components_

### 投影数据

我们可以将数据投影到主成分上，以获得降维后的数据。

data_reduced = np.dot(data_std, components.T)

### 可视化结果

最后，我们可以可视化原始数据和降维后的数据。

plt.scatter(data[:, 0], data[:, 1], label='Original data')
plt.scatter(data_reduced[:, 0], data_reduced[:, 1], label='Reduced data')
plt.legend()
plt.show()

### 代码逻辑逐行解读

- `import numpy as np`: 导入NumPy库，用于数值计算。
- `import sklearn.decomposition as decomp`: 导入Scikit-learn库中的降维模块。
- `import matplotlib.pyplot as plt`: 导入Matplotlib库，用于可视化。
- `data = np.loadtxt('data.csv', delimiter=',')`: 从CSV文件中加载数据集，以逗号作为分隔符。
- `data_std = (data - np.mean(data, axis=0)) / n