辅助疾病诊断：PCA降维算法在医疗诊断中的应用

# 1. PCA降维算法概述**

PCA（主成分分析）是一种降维算法，用于将高维数据投影到低维空间，同时保留原始数据中的最大方差。它通过对数据进行线性变换，找到一组正交基向量，这些基向量对应于数据中方差最大的方向。

PCA降维的优势在于：

- **数据压缩：**通过减少数据维度，可以降低存储和处理成本。
- **特征提取：**PCA可以提取数据中最重要的特征，有助于识别模式和异常值。
- **可视化：**降维后的数据可以更直观地进行可视化，便于探索和分析。

# 2.1 PCA降维算法的基本原理

PCA（主成分分析）是一种经典的降维算法，其基本原理是将原始高维数据投影到一个低维子空间，使得投影后的数据在保留原始数据主要信息的同时，维度大大降低。

PCA算法的具体步骤如下：

1. **数据标准化：**对原始数据进行标准化处理，消除不同特征之间的量纲差异。
2. **协方差矩阵计算：**计算原始数据协方差矩阵，反映各特征之间的相关性。
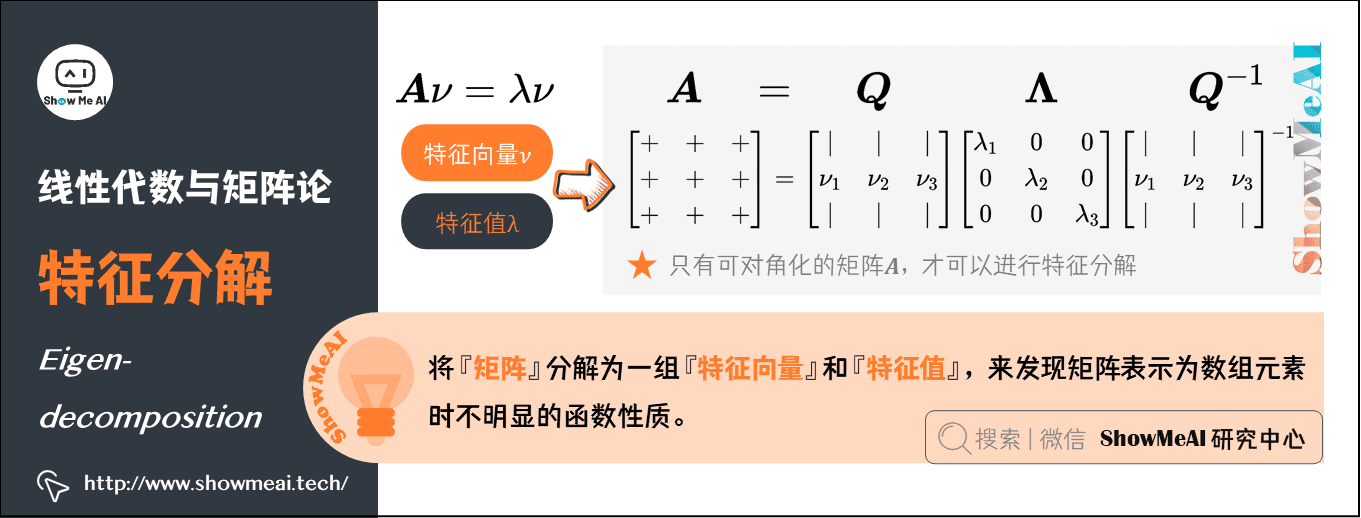
3. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. **特征向量排序：**按照特征值从大到小的顺序对特征向量进行排序，前k个特征向量构成投影矩阵。
5. **数据投影：**将原始数据与投影矩阵相乘，得到降维后的数据。

### PCA降维算法的参数说明

PCA算法的参数主要包括：

- **k：**投影后的维度，即主成分的个数。
- **特征值阈值：**用于选择主成分的阈值，通常选择大于某个阈值的特征值对应的特征向量。

### PCA降维算法的逻辑分析

PCA算法的逻辑分析如下：

- **数据标准化：**消除量纲差异，确保各特征在投影过程中具有同等重要性。
- **协方差矩阵计算：**反映特征之间的相关性，为特征值分解提供基础。
- **特征值分解：**提取原始数据中方差最大的方向，即主成分。
- **特征向量排序：**选择方差最大的k个主成分，保留原始数据的主要信息。
- **数据投影：**将原始数据投影到主成分构成的子空间，实现降维。

### PCA降维算法的优势

PCA降维算法在医疗诊断中具有以下优势：

- **信息保留：**PCA算法可以有效保留原始数据的主要信息，避免信息丢失。
- **维度降低：**PCA算法可以大大降低数据的维度，简化后续分析和处理。
- **鲁棒性：**PCA算法对异常值和噪声具有较好的鲁棒性，能够有效去除干扰信息。
- **可解释性：**PCA算法的主成分具有明确的物理意义，便于解释和理解。

# 3. PCA降维算法在医疗诊断中的应用实践

### 3.1 医疗数据预处理和特征提取

医疗数据通常存在噪声、缺失值和冗余等问题，在应用PCA降维算法之前，需要对数据进行预处理和特征提取。

#### 数据预处理

数据预处理包括以下步骤：

- **数据清洗：**去除异常值、缺失值和噪声。
- **数据标准化：**将不同特征的数据缩放至同一量级，消除量纲差异的影响。
- **数据归一化：**将数据映射到[0, 1]区间内，增强数据可比性。

#### 特征提取

特征提取是将原始数据中的冗余和无关信息去除，提取出具有代表性的特征。常用的特征提取方法包括：

- **主成分分析（PCA）：**通过线性变换将原始数据投影到低维空间，提取出方差最大的主成分。
- **奇异值分解（SVD）：**将数据分解为奇异值、左奇异向量和右奇异向量，提取出数据中的主要模式。
- **独立成分分析（ICA）：**将数据分解为统计独立的成分，提取出数据中的隐藏模式。

### 3.2 PCA降维算法的实现和参数选择

PCA降维算法的实现步骤如下：

1. 对数据进行中心化，即减去每个特征的均值。
2. 计算协方差矩阵或相关矩阵。
3. 对协方差矩阵或相关矩阵进行特征值分解，得到特征值和特征向量。
4. 选择前k个特征值对应的特征向量作为主成分。

PCA降维算法的参数选择主要包括：

- **主成分个数：**根据业务需求和数据特性选择保留的主成分个数。
- **特征值阈值：**设置一个阈值，只保留特征值大于阈值的特征向量作为主成分。
-