识别市场趋势：PCA降维算法在金融数据分析中的应用

# 1. PCA降维算法概述

PCA（主成分分析）是一种经典的降维算法，用于将高维数据投影到低维空间，同时保留原始数据的关键信息。PCA通过线性变换将原始数据映射到一组正交基向量（主成分）上，这些基向量代表了数据中最大的方差方向。

PCA算法的优点包括：

- **数据降维：**将高维数据投影到低维空间，减少数据存储和处理的成本。
- **信息保留：**通过选择主成分，PCA保留了原始数据中最重要的信息。
- **可解释性：**主成分可以解释为数据中方差最大的方向，便于理解数据的结构。

# 2. PCA降维算法原理与实现

### 2.1 PCA降维算法的数学原理

#### 2.1.1 协方差矩阵与特征值分解

PCA降维算法的核心思想是通过寻找原始数据中方差最大的方向，将数据投影到这些方向上，从而达到降维的目的。数学上，可以通过计算协方差矩阵来寻找这些方向。

协方差矩阵是一个对称矩阵，其元素表示不同特征之间的协方差。对于一个n维数据集，其协方差矩阵C是一个n×n矩阵，元素c_ij表示特征i和特征j之间的协方差，计算公式为：

import numpy as np

def covariance_matrix(X):
  """计算协方差矩阵。

  Args:
    X: 输入数据，形状为(n, m)，其中n为样本数，m为特征数。

  Returns:
    协方差矩阵，形状为(m, m)。
  """

  n, m = X.shape
  cov = np.zeros((m, m))
  for i in range(m):
    for j in range(m):
      cov[i, j] = np.cov(X[:, i], X[:, j])[0, 1]
  return cov

协方差矩阵的特征值分解可以得到一组特征值和对应的特征向量。特征值表示协方差矩阵中每个方向的方差，特征向量表示这些方向。

import numpy as np

def eigenvalue_decomposition(C):
  """进行特征值分解。

  Args:
    C: 协方差矩阵，形状为(m, m)。

  Returns:
    特征值，形状为(m,)。
    特征向量，形状为(m, m)。
  """

  eigenvalues, eigenvectors = np.linalg.eig(C)
  return eigenvalues, eigenvectors

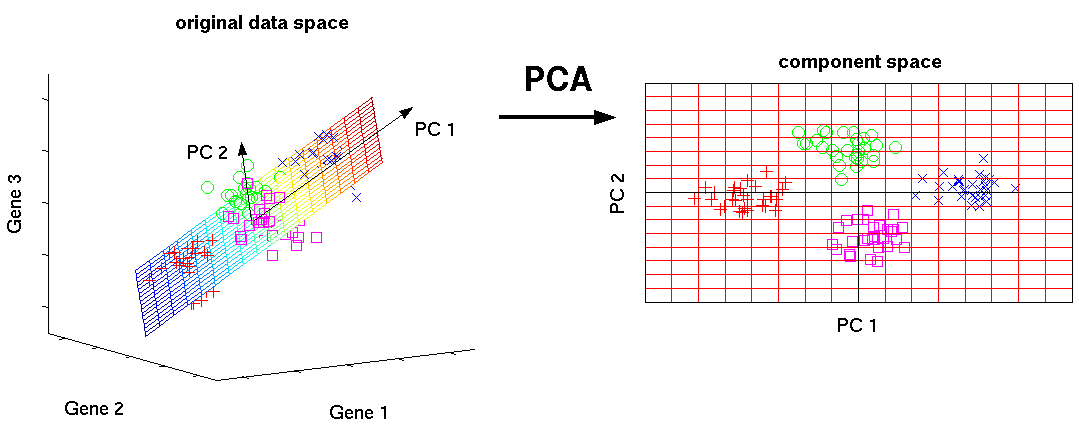
#### 2.1.2 主成分分析的几何解释

从几何角度来看，PCA降维算法就是将原始数据投影到特征向量所张成的子空间中。投影后的数据称为主成分，主成分的方差从大到小排列。

对于一个n维数据集，PCA降维算法可以将数据投影到k维子空间中，其中k小于n。投影后的数据称为k维主成分，其方差从大到小排列。

### 2.2 PCA降维算法的Python实现

#### 2.2.1 NumPy库中的PCA实现

NumPy库提供了`linalg.svd`函数进行奇异值分解，奇异值分解的结果可以用来计算特征值和特征向量。

import numpy as np

def pca_numpy(X, k):
  """使用NumPy库实现PCA降维。

  Args:
    X: 输入数据，形状为(n, m)，其中n为样本