处理海量数据：PCA降维算法在高维数据分析中的应用

# 1. 高维数据分析中的挑战**

高维数据分析是当今大数据时代面临的重大挑战。随着数据量的不断增长，数据维度也随之增加。高维数据给数据分析带来了以下挑战：

- **计算复杂度高：**高维数据中的计算量呈指数级增长，导致算法运行时间过长。
- **数据稀疏性：**高维数据中，数据点往往分布在高维空间的稀疏区域，使得数据分析难以有效进行。
- **维度灾难：**当数据维度过高时，数据点的距离和相似度等概念变得难以定义和计算。

# 2. PCA降维算法原理

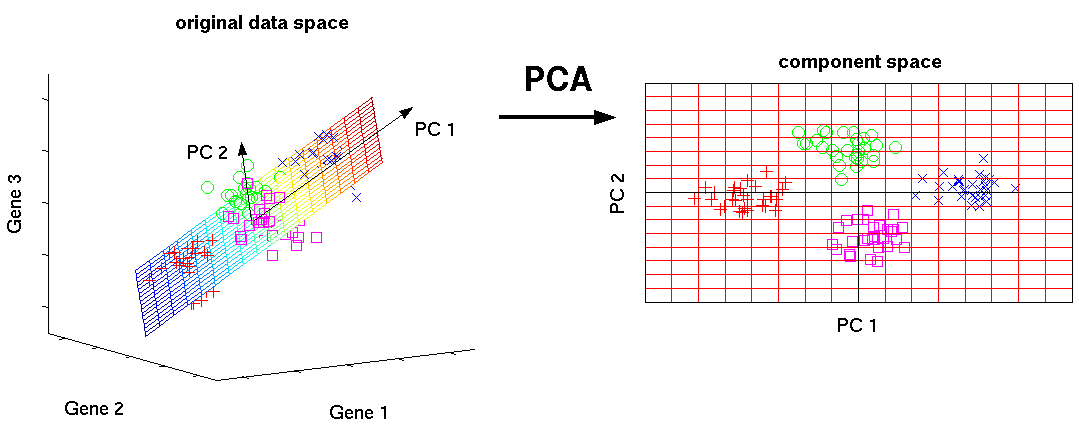
PCA（主成分分析）是一种经典的降维算法，广泛应用于高维数据分析中。其基本原理是通过线性变换将高维数据投影到低维空间，从而保留原始数据中最重要的信息。

### 2.1 线性代数基础

PCA算法的基础是线性代数。以下是一些关键概念：

- **向量：**一个有序的数字序列，表示数据点在坐标系中的位置。
- **矩阵：**一个数字表格，表示一组向量之间的关系。
- **协方差矩阵：**一个矩阵，表示一组向量之间的协方差。
- **特征值和特征向量：**协方差矩阵的特征值表示数据方差的方向，特征向量表示这些方向。

### 2.2 协方差矩阵和特征值分解

协方差矩阵描述了数据集中变量之间的协方差。对于一个给定的数据集，协方差矩阵是一个对称矩阵，其元素表示变量之间的协方差。

特征值分解是一种线性代数技术，可以将协方差矩阵分解为特征值和特征向量。特征值表示数据方差的方向，特征向量表示这些方向。

### 2.3 PCA降维过程

PCA降维过程包括以下步骤：

1. **计算协方差矩阵：**计算数据集的协方差矩阵。
2. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。
3. **选择主成分：**选择特征值最大的特征向量作为主成分。
4. **投影数据：**将原始数据投影到主成分空间，得到降维后的数据。

**代码块：**

import numpy as np

# 计算协方差矩阵
covariance_matrix = np.cov(data)

# 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)

# 选择主成分
num_components = 2  # 降维到 2 维
principal_components = eigenvectors[:, :num_components]

# 投影数据
reduced_data = np.dot(data, principal_components)

**逻辑分析：**

* `np.cov()` 函数计算数据集的协方差矩阵。
* `np.linalg.eig()` 函数对协方差矩阵进行特征值分解，得到特征值和特征向量。
* `eigenvalues` 数组包含特征值，`eigenvectors` 数组包含特征向量。
* `num_components` 变量指定要降维到的维度数。
* `principal_components` 变量包含主成分，即特征值最大的特征向量。
* `np.dot()` 函数将原始