【故障排除宝典】：拓扑排序常见问题及调试攻略

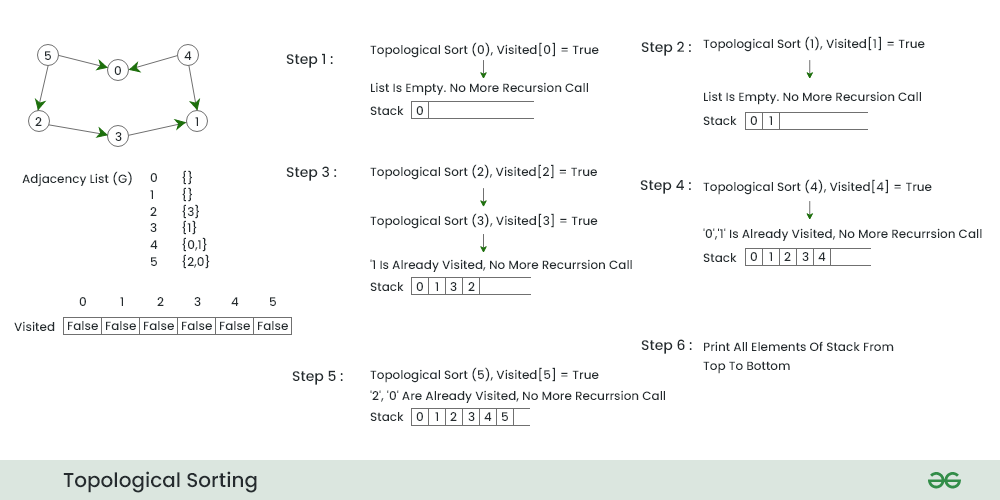
# 1. 拓扑排序概念解析

在计算机科学领域，拓扑排序是一种将有向无环图（DAG）中所有顶点排成一个线性序列的过程，使得对于任何一条有向边(u, v)，顶点u都在顶点v之前。这个概念对于理解依赖关系以及在项目调度、软件构建系统和其他需要处理依赖顺序的系统中至关重要。

拓扑排序的概念虽然看似简单，但它背后反映的是对复杂系统中元素顺序关系的一种抽象。通过拓扑排序，我们可以清晰地看到各个元素之间的先后执行顺序，从而设计出高效的算法来处理它们。

在下一章中，我们将深入了解拓扑排序的理论基础，探讨其定义、目的、应用场景、算法原理以及与其他排序方法的比较，这将为我们提供一个更全面的视角来认识和运用拓扑排序。

# 2. 拓扑排序的理论基础

## 2.1 拓扑排序的基本定义

### 2.1.1 有向无环图(DAG)的引入
有向无环图（DAG）是由顶点集合和有向边集合构成的图，其中任意两个顶点间由唯一的一条路径相连。DAG是拓扑排序的基础数据结构，因为只有在没有环的图中，我们才能定义顶点的先后顺序。

在DAG中，如果从顶点A到顶点B存在一条有向边（A, B），那么我们说顶点A在顶点B的前面，或者说B依赖于A。例如，表示课程表的图，节点可以代表课程，有向边表示课程的先决条件。

DAG的引入，使得我们可以为具有依赖关系的任务或数据项定义一个顺序，这在项目管理、软件构建依赖、编译器的依赖分析等领域有着广泛的应用。

### 2.1.2 拓扑排序的目的和应用场景
拓扑排序的主要目的是将DAG的所有顶点线性排序，使得对于图中的每一条有向边(u, v)，顶点u都在顶点v之前。这种排序不是唯一的，但任何有效的拓扑排序都能反映DAG的依赖关系。

拓扑排序广泛应用于需要处理依赖关系的场合。以下是一些典型的应用场景：
- **课程表编排**：每个学生都需要按照课程的先决条件来安排学习计划。
- **软件构建系统**：如Maven和Gradle这样的构建工具在构建项目时，需要按照依赖关系对任务进行排序。
- **任务调度**：在任务依赖图中，确保任务按照逻辑顺序执行，避免依赖性冲突。
- **计算机图形学**：拓扑排序可以帮助处理场景图和渲染顺序。
- **事件驱动编程**：确保事件以正确的顺序发生，例如在UI组件的初始化和渲染过程中。

## 2.2 拓扑排序的算法原理

### 2.2.1 入度和出度的概念
在有向图中，顶点的入度指的是指向该顶点的边的数量，出度指的是从该顶点出发的边的数量。例如，A -> B，A的出度是1，B的入度是1。

在拓扑排序中，顶点的入度尤为重要，因为它表示了一个顶点在排序中的位置依赖于多少其他顶点。当一个顶点的入度为0，意味着没有任何顶点依赖于它，因此它可以在排序中排在前面。

### 2.2.2 拓扑排序的主要算法及步骤
拓扑排序通常可以使用两种主要算法来实现：Kahn算法和深度优先搜索（DFS）算法。这里我们重点介绍Kahn算法。

Kahn算法的主要步骤如下：

1. 计算图中每个顶点的入度。
2. 将所有入度为0的顶点放入队列中。
3. 当队列非空时，执行以下步骤：
a. 从队列中取出一个顶点，并输出该顶点。
b. 遍历该顶点的所有邻接顶点，将它们的入度减1，如果减1后入度为0，则将邻接顶点放入队列。
4. 重复步骤3直到队列为空。如果所有顶点都被输出，则算法结束，得到一个有效的拓扑排序；如果队列为空但还有顶点未被输出，则说明图中存在环，无法进行拓扑排序。

### 2.2.3 算法的时间复杂度分析
Kahn算法的时间复杂度主要由以下操作决定：
- 计算所有顶点的入度：O(V+E)，V是顶点数，E是边数。
- 遍历队列中的每个顶点，并更新其邻接顶点的入度：O(V+E)。
- 输出排序结果：O(V)。

因此，总的复杂度为O(V+E)，这是一个线性时间复杂度的算法，适合处理大型图。

## 2.3 拓扑排序与其他排序方法的比较

### 2.3.1 拓扑排序与线性排序的区别
拓扑排序与线性排序（如快速排序、归并排序等）的主要区别在于排序对象的性质：
- **线性排序**：处理的是离散的元素，没有依赖关系，可以任意交换元素的位置。
- **拓扑排序**：处理的是具有依赖关系的数据项，需要保持依赖关系的正确性。

线性排序强调的是元素间的相对位置，而拓扑排序强调的是元素间的依赖关系，不能随意交换位置。

### 2.3.2 拓扑排序与树形结构排序的联系
拓扑排序可以看作是树形结构排序的推广。在树形结构中，每个节点只有一个父节点，排序相对简单。在拓扑排序中，节点可能有多个父节点，需要考虑整个图的全局依赖关系。

拓扑排序与树形结构排序的联系在于，它们都试图对元素进行一种线性排序，而且都可以通过算法实现。然而，拓扑排序处理的图结构更加复杂，算法实现也相应更为复杂。

在下一章节中，我们将深入探讨拓扑排序的实践技巧，包括编程语言的选择、编程实践以及应用案例分析。

# 3. 拓扑排序实践技巧

## 3.1 实现拓扑排序的编程语言选择

### 3.1.1 选择合适的编程语言概述

在实现拓扑排序算法时，选择合适的编程语言至关重要。不同的编程语言有着各自的特点，如执行速度、语法的简洁性、库函数的丰富程度等，这些都可能对拓扑排序的实现和优化产生影响。

比如，C++因其高性能通常用于需要优化运行时间的应用场景，而Python以其简洁的语法和丰富的库支持在快速原型开发中更为突出。Java则在企业级应用和跨平台开发中占有优势。JavaScript常用于前端开发和Node.js服务器端的开发，适合实现具有并发需求的拓扑排序。

### 3.1.2 不同语言实现拓扑排序的优劣分析

不同编程语言实现拓扑排序各有优劣，以下是一个比较分析：

- **C++**：C++提供了STL（标准模板库），其中包含的`vector`和`queue`等容器非常适合实现拓扑排序算法。由于其接近底层的特性，C++编写的算法执行速度非常快，非常适合算法竞赛和性能敏感的应用。但是，C++的语法相对复杂，对于初学者来说可能存在较高的学习门槛。

- **Python**：Python的语法简洁明了，易于理解和使用。对于算法的原型设计来说，Python是一个很好的选择。它内置的数据结构足以支持拓扑排序的实现，而且有着丰富的第三方库支持。然而，Python的执行效率并不如C++或Java，对于大数据集处理时可能会遇到性能瓶颈。

- **Java**：Java具有跨平台的特性，能够“一次编写，到处运行”，这使得Java实现的拓扑排序算法可以非常方便地部署到不同的操作系统中。Java的标准库也提供了丰富的数据结构和算法实现，例如`ArrayList`和`LinkedList`。但是，Java相较于C++会有更大的运行时开销，尤其在内存管理方面。

- **JavaScript**：JavaScript通常用于网络应用开发，但它的并发处理能力和Node.js的支持，使得JavaScript也适合实现拓扑排序。JavaScript的异步和事件驱动特性，可以在某些场景下进行有效的性能优化。

## 3.2 拓扑排序的编程实践

### 3.2.1 编写拓扑排序算法的代码框架

下面提供一个使用Python实现的拓扑排序的代码框架，该框架包含了构建有向图和执行排序的逻辑：

from collections import defaultdic