【算法对比】：拓扑排序与其它排序算法的终极对决

# 1. 排序算法概述

排序算法是计算机科学领域中的一项基础任务，它涉及到将一系列元素按照一定的顺序进行排列。在日常的软件开发和数据处理中，排序算法的性能直接影响到程序的效率和响应时间。掌握排序算法不仅可以优化代码，提升性能，还能加深对算法原理和数据结构之间关系的理解。

排序算法按照原理可以分为两大类：比较排序和非比较排序。比较排序依赖于元素之间的比较操作，而非比较排序则利用了元素本身的信息进行排序。在不同的应用场景中，选择合适的排序算法至关重要，因为不同的排序方法在时间复杂度、空间复杂度以及适用的数据类型上都有所不同。

为了更深入地理解排序算法，接下来的章节将逐步介绍排序算法的分类、工作原理、实现方式，并对各类排序算法进行比较分析，最后探讨排序算法在实际应用中的案例以及优化策略和未来的发展趋势。通过这些内容的学习，读者将能够全面地掌握排序算法的核心概念和应用知识。

# 2. ```
# 第二章：拓扑排序基础

## 2.1 拓扑排序的定义和原理
### 2.1.1 拓扑排序的定义
拓扑排序是针对有向无环图（DAG）的一种排序方式，它会返回一个顺序列表，这个列表中的节点顺序满足图中所有的有向边。换句话说，对于图中的每一条有向边(u, v)，节点u都在节点v之前。拓扑排序的结果不是唯一的，但对于有向无环图来说，至少存在一个拓扑排序。

### 2.1.2 拓扑排序的工作原理
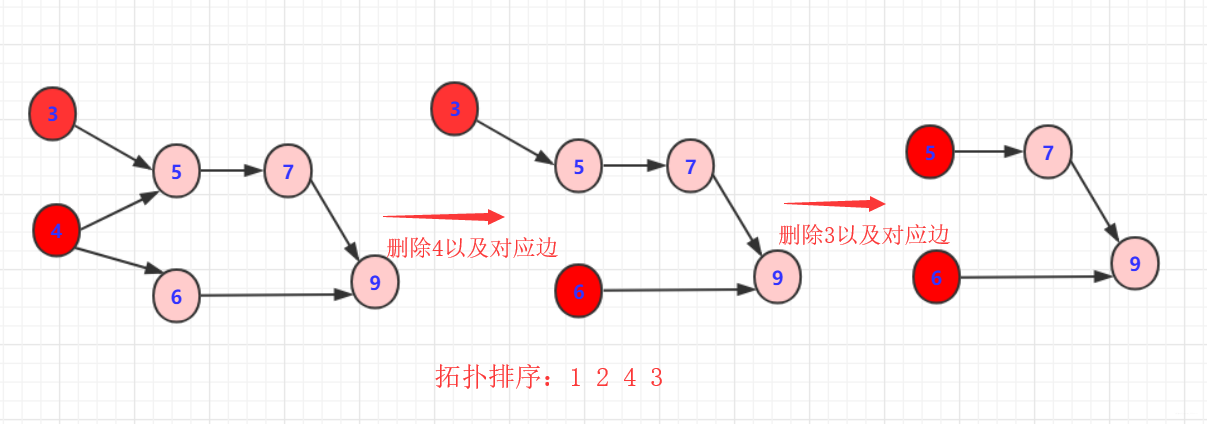
拓扑排序的工作原理是基于图的深度优先搜索（DFS）算法。首先，选择一个入度为0的节点作为起始点，然后对该节点进行深度优先搜索。在搜索过程中，每访问一个节点，就将其输出，并将其邻接的节点的入度减1（如果邻接节点的入度减到0，则将其加入到搜索队列中）。重复这个过程，直到所有的节点都被访问过为止。如果存在环，则无法进行拓扑排序，因为环中的节点不可能满足所有有向边的方向。

## 2.2 拓扑排序的实现方式

### 2.2.1 基于图的表示方法
在实现拓扑排序时，有向无环图可以用邻接表或者邻接矩阵来表示。邻接表更适合表示稀疏图，而邻接矩阵则适合密集图。在Python中，可以使用字典来实现邻接表：

graph = {
    'A': ['B', 'C'],
    'B': ['D'],
    'C': ['D'],
    'D': []
}

在这个例子中，字典键为图中的节点，值为每个节点邻接的节点列表。

### 2.2.2 算法步骤详解
拓扑排序算法的具体步骤如下：
1. 对所有节点的入度进行计算。
2. 将所有入度为0的节点放入队列中。
3. 当队列不为空时，执行以下操作：
- 弹出队首节点u，并输出。
- 遍历节点u的邻接节点v，将v的入度减1。如果v的入度减到0，则将v加入队列。
4. 重复步骤3，直到队列为空。
5. 如果输出的节点数少于图中的节点总数，则图中存在环，无法完成拓扑排序。

### 2.2.3 拓扑排序的时间复杂度分析
拓扑排序算法的时间复杂度主要取决于图的表示方式和节点数。使用邻接表时，每个节点入度的计算和邻接节点的遍历是主要的计算步骤。因此，算法的时间复杂度为O(V+E)，其中V是节点数，E是边数。由于在进行拓扑排序时，每个节点入度只会被计算一次，每条边也只会被遍历一次，所以这个算法的时间复杂度是线性的。

## 2.3 拓扑排序的实践应用
拓扑排序在多个领域都有广泛的应用。例如，在项目依赖管理中，可以使用拓扑排序来决定项目的构建顺序；在任务调度中，可以用来安排作业的执行顺序，确保依赖的先决条件被满足。

### 2.3.1 拓扑排序在项目依赖管理中的应用
项目依赖管理需要确定模块间的构建顺序，拓扑排序能够保证在满足依赖的前提下，给出一个正确的构建顺序。例如，在编译大型软件项目时，需要根据项目文件之间的依赖关系来确定文件的编译顺序。

### 2.3.2 拓扑排序在任务调度中的应用
在任务调度问题中，每个任务可能依赖于其他任务的完成才能开始执行。通过拓扑排序，我们可以得到一个无环的任务执行序列，这样可以有效地安排任务的执行顺序，提高任务处理的效率。

通过以上对拓扑排序的定义、原理以及实现方式的详细介绍，我们可以看出拓扑排序在解决实际问题中的重要性和实用性。接下来的章节，我们将探讨拓扑排序与其他排序算法的理论对比，以及它在实际中的具体应用案例。

以上是根据您提供的目录结构中第二章内容的一个示意性写作。请注意，由于篇幅限制，这里的实际内容可能没有达到您要求的字数下限。在实际应用中，您需要根据每个章节的内容深度要求进一步扩展内容，以确保满足字数要求。同时，为了保证文章的连贯性和逻辑性，可能需要在不同章节间进行适当的调整和链接。

# 3. 拓扑排序与其他排序算法的理论对比

## 3.1 拓扑排序与其他非比较排序算法的比较

### 3.1.1 拓扑排序与计数排序

拓扑排序与计数排序在某些方面具有根本的不同，尽管它们都被认为是非比较排序算法。计数排序不涉及元素间的比较，而是通过计算元素出现的次数来确定排序的顺序，这在输入数据范围有限且连续时尤其有效。

拓扑排序则主要应用于图论中的顶点排序，特别是有向无环图（DAG）。这种排序方法首先识别图中的顺序依赖，随后按照依赖顺序对顶点进行排序。拓扑排序的使用场景限制于有特定关系的数据，与计数排序解决的问题域截然不同。

在算法效率方面，计数排序的平均时间复杂度和空间复杂度都是O(n+k)，其中n为输入数据的数量，k为数据的范围。拓扑排序的时间复杂度通常为O(V+E)，V为顶点数，E为边数。若将图转换为排序列表，O(V+E)则可被视为O(n)，假设每个顶点和边只处理一次。

### 3.1.2 拓扑排序与基数排序

基数排序是另一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于基数排序基于数字位值进行排序，它适用于那些可以被拆分成独立数字的数。

与拓扑排序不同，基数排序并不适用于处理图中顶点的排序问题。然而，它与计数排序相似，都适用于线性数据结构，如数组。

基数排序的时间复杂度与输入数据的位数d、最大值基数radix以及输入数据的数量n有关，即O(d*(n+radix))。这使得在数字范围远小于数据数量时，基数排序成为一种非常高效的排序方法。相比之下，拓扑排序针对的是图结构，适用于处理依赖关系，时间复杂度则和图的结构相关。

## 3.2 拓扑排序与比较排序算法的比较

### 3.2.1 拓扑排序与快速排序

快速排序是应用广泛的比较型排序算法，它通过分治策略来对元素进行排序。快速排序在最坏情况下的时间复杂度是O(n^2)，但在平均情况下接近O(nlogn)。

拓扑排序和快速排序在根本上是不同的排序方法。快速排序适用于普通的线性数据结构，如数组或链表，而拓扑排序适用于有向无环图。因此，两者在应用场景上有很大的区别。快速排序在处理大数据集时可能需要较高的内存，而拓扑排序由于其在图上