【大数据优化】：拓扑排序算法性能提升的4大策略

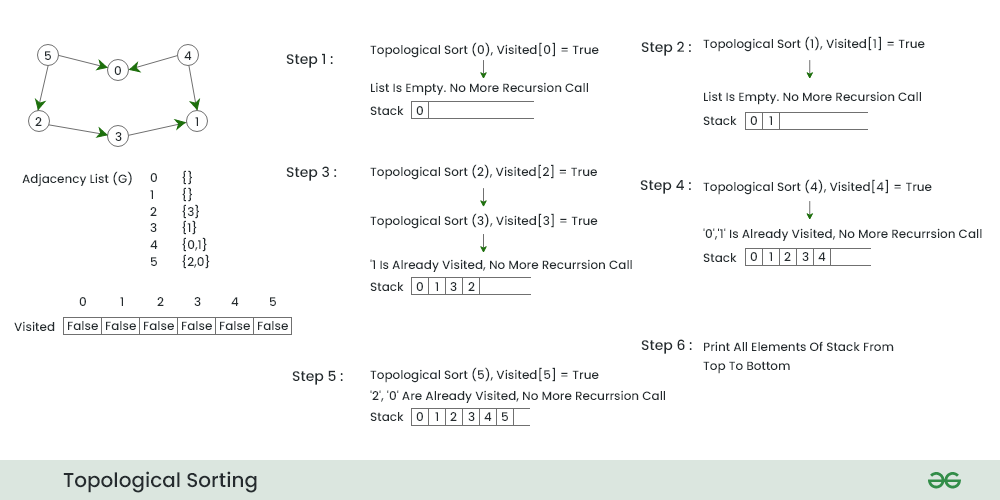
# 1. 拓扑排序算法概述

拓扑排序是图论中用于表示有向无环图（DAG）顶点线性序列的算法，它按照边的流向将顶点排列成一个有序序列，使得对于任意一条图中的有向边(u, v)，顶点u都在顶点v之前。这种排序方式在许多场景中都有广泛应用，例如在项目管理、软件包依赖关系解析等领域。

## 1.1 算法定义和应用场景

拓扑排序是计算机科学中非常基础且重要的概念之一。它不仅可以帮助我们理解和处理项目依赖关系，还可以在很多不同的领域应用，比如编译器中的语句执行顺序安排、课程表的制定等。

## 1.2 拓扑排序的实现思路

拓扑排序通常有两种实现方式：Kahn算法和深度优先搜索（DFS）。Kahn算法适用于所有顶点的入度信息已知的情况，而DFS方法则是递归地选择入度为0的顶点进行排序。两种方法虽然实现思路不同，但最终目标都是生成一个顶点的线性序列。

以Kahn算法为例，其步骤如下：
1. 计算每个顶点的入度（即有多少条边指向该顶点）。
2. 将所有入度为0的顶点放入一个队列中。
3. 当队列非空时，执行循环：
a. 弹出队列中的一个顶点。
b. 对于弹出顶点所指向的每一个邻接点，将其入度减1。
c. 若邻接点的入度减为0，则将其加入队列。
4. 如果所有顶点都被正确排序，则该序列即为拓扑排序的结果。

本章为您梳理了拓扑排序算法的基础知识，为后续的性能基准测试与优化分析打下了坚实的基础。

# 2. 性能基准测试与分析

## 2.1 拓扑排序算法的基准测试方法

### 2.1.1 选择基准测试工具

进行拓扑排序算法的性能测试，首先需要选择合适的基准测试工具。基准测试工具的选择应该基于以下几点：

- **兼容性**：测试工具应与算法开发的编程语言兼容。
- **灵活性**：工具应允许自定义测试参数，如输入数据的规模和特性。
- **可扩展性**：在面对不同场景时，测试工具应能提供足够的性能数据，如CPU使用率、内存消耗和算法运行时间。
- **精确度**：测量结果应具备高精确度，以便进行准确的性能评估。
- **易用性**：工具应直观易用，减少学习成本，提高测试效率。

常见的基准测试工具包括但不限于`Apache JMeter`（对于Java应用）、`Google Benchmark`（C++）、`PyBench`（Python）。选择合适的工具，可以确保在后续的性能测试中获得可靠的数据。

### 2.1.2 设计测试案例和场景

设计测试案例和场景是基准测试中至关重要的环节。测试案例需要覆盖算法在不同条件下的性能表现：

- **测试案例设计**：要设计不同的输入数据集，以考察算法在不同数据规模和结构下的表现。
- **场景模拟**：模拟现实世界的使用场景，例如，处理大规模图数据、进行实时拓扑排序等。

一个合理的测试案例应该包括以下几种情况：

- **小规模数据**：测试算法在简单情况下的基本性能。
- **大规模数据**：测试算法在高负载时的性能和扩展性。
- **极端情况**：测试算法在数据结构异常复杂或存在大量循环依赖时的表现。

此外，测试场景应该包括：

- **单线程测试**：在单线程环境下测试算法的性能。
- **多线程测试**：在多线程环境下测试算法的性能，考察并发处理能力。

## 2.2 算法性能的度量标准

### 2.2.1 时间复杂度分析

时间复杂度是衡量算法性能的首要指标，反映了算法在处理输入数据时随数据规模变化的增长趋势。

拓扑排序算法在理想情况下的时间复杂度为O(V+E)，V表示顶点数，E表示边数。这意味着算法的性能与顶点数量和边的数量呈线性关系。

在基准测试中，应该记录并比较在不同大小的数据集上算法的实际运行时间，以便于分析时间复杂度的理论值与实际值之间的差异。这有助于揭示潜在的性能瓶颈，为算法的进一步优化提供依据。

### 2.2.2 空间复杂度分析

空间复杂度与时间复杂度同样重要，它衡量算法在执行过程中所需的存储空间。

对于拓扑排序算法，空间复杂度主要取决于存储图结构所需的内存空间。在有向无环图（DAG）中，空间复杂度至少为O(V+E)，因为需要存储所有顶点和边。

在进行基准测试时，应记录算法执行过程中的最大内存使用量，并分析其随数据规模变化的趋势。这有助于了解算法的内存使用效率，并指导后续的内存优化工作。

## 2.3 测试结果与瓶颈识别

### 2.3.1 实验数据的收集与可视化

实验数据的收集是基准测试的一个关键环节。收集的数据类型应包括：

- 算法的执行时间。
- 内存使用情况。
- CPU占用率。
- 输入数据规模（顶点数和边数）。
- 系统负载情况（如I/O操作等）。

数据收集的方法可以使用系统内置的性能监控工具，或者在编写测试代码时内置日志记录功能。收集到的数据应该进行整理，便于后续分析。

数据可视化是理解测试结果的关键步骤。可以使用`Excel`图表、`Matplotlib`库（Python）、`ggplot2`库（R语言）等工具生成柱状图、折线图、散点图等，直观地展示数据的变化趋势。

### 2.3.2 瓶颈问题的定位与分析

在获得基准测试的数据和可视化结果后，接下来是识别性能瓶颈并进行分析。

- **瓶颈定位**：通过比较不同测试案例的结果，找出算法性能明显下降的点。
- **分析过程**：结合算法执行的内部逻辑，分析为什么在某些案例下性能不佳。可能的原因包括数据结构选择不当、算法逻辑复杂度过高、内存管理不善、CPU缓存未优化等。

一旦识别出瓶颈，应该采取相应的优化措施，如改进数据结构、优化算法逻辑、提高内存使用效率、改善CPU缓存利用率等，然后重新进行基准测试，以验证优化的效果。通过这样的循环，可以逐步提高算法的性能。

下一章，我们将探讨基础优化策略，这些策略是解决性能瓶颈问题的关键所在。

# 3. ```
# 第三章：基础优化策略

## 3.1 数据结构的选择与优化
在实现拓扑排序算法时，选择合适的数据结构对于提升算法效率至关重要。数据结构不仅影响代码的复杂性，还决定了算法的时间和空间性能。

### 3.1.1 适应场景的数据结构

针对拓扑排序，图的表示方式将直接影响算法的执行效率。例如，邻接矩阵适合稠密图的表示，而邻接表则更适合稀疏图。邻接表因为其在表示稀疏图时的空间优势，通常用于大型网络中节点关系不紧密的情况，能有效减少不必要的存储开销。

class Graph {
    int vertices; // 图中顶点的数量
    LinkedList<Integer>[] adjacencyLists; // 邻接表表示

    Graph(int vertices) {
        this.vertices = vertices;
        adjacencyLists = new LinkedList[vertices];
        for (int i = 0; i < vertices; i++) {
            adjacencyLists[i] = new LinkedList<>();
        }
    }

    // 添加边
    public void addEdge(int source, int destination) {
        adjacencyLists[source].add(destination);
    }
}

上述代码表示了一个使用邻接表数据结构的图类，其中`vertices`存储顶点数量，`adjacencyLists`为邻接表数组。

### 3.1.2 结构优化的理论依据

优化数据结构需要考虑算法的执行流程和数据访问模式。在拓扑排序中，我们经常需要快速访问入度为零的顶点。因此，一个带入度数组的数据结构将非常有用，它允许我们以O(1)的时间复杂度访问入度为零的顶点，从而加快排序过程。

class Graph {
    int[] inDegree; // 存储每个顶点的入度信息

    Graph(int vertices) {
        inDegree = new int[vertices];
    }

    // 更新顶点入度
    public void addEdge(int source, int destination) {
        inDegree[destination]++;
    }
}

上述代码扩展了图类以包含顶点的入度信息，有助于快速确定哪些顶点可以被排序。

## 3.2 算法逻辑简化与重组

为了提高算法效率，我们可以对算法逻辑进行简化和重组。在拓扑排序中，常见的逻辑优化包括使用优先队列（最小堆）来处理入度为零的顶点。

### 3.2.1 逻辑简化的方法

传统拓扑排序使用队列来存储所有入度为零的顶点。然而，如果我们使用优先队列来存储这些顶点，就可以利用其天然的排序特性进一步提高效率。

PriorityQueue<Integer>