【变种探索】：拓扑排序的多种形态与应用场景

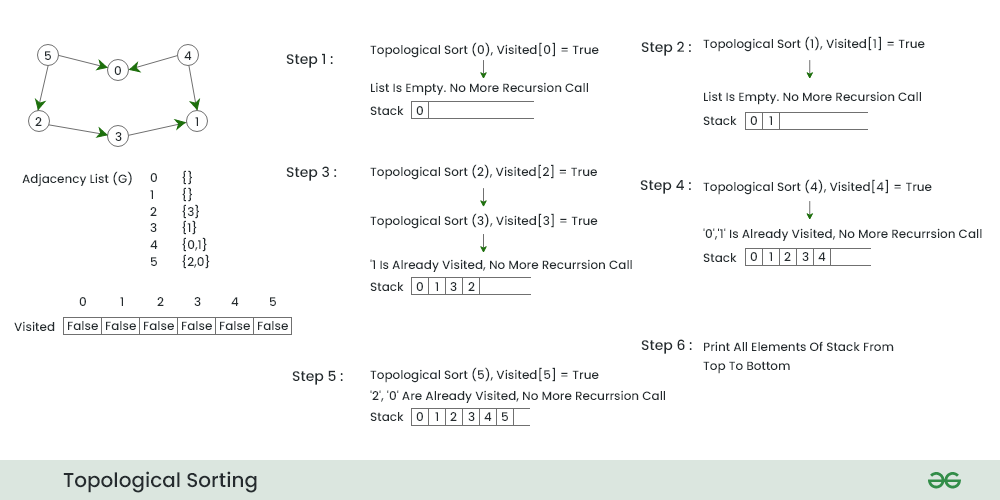
# 1. 拓扑排序概述

拓扑排序是图论中的一个经典问题，它针对的是有向无环图（DAG）。在这类图中，每一条边都有明确的方向，指向顶点间的依赖关系。拓扑排序能够将图中的顶点组织成一个线性序列，使得对于任意一条有向边(u, v)，顶点u总是在顶点v之前出现。这一特性使得拓扑排序广泛应用于依赖关系的管理，比如在软件开发中管理项目依赖、在教育系统中安排课程顺序等。通过将复杂的依赖结构简化为有序序列，拓扑排序有助于我们更清晰地理解系统之间的相互作用和依赖层次，提高整体的管理和执行效率。

# 2. 拓扑排序的基本原理

### 2.1 有向无环图（DAG）简介

#### 2.1.1 DAG的定义与特性
有向无环图（DAG）是图论中的一个重要概念，它由一组顶点（vertices）和一组有方向的边（edges）组成，边的方向由一个顶点指向另一个顶点。DAG的一个关键特性是不存在任何顶点到其自身的边，即不存在环（cycle）。DAG在解决依赖、流程控制以及递归算法等多个领域都有广泛的应用。

graph TD
    A --> B
    A --> C
    B --> D
    C --> D

上述代码块展示了用Mermaid语法绘制的一个简单的DAG示例，其中顶点A、B、C和D通过有方向的边连接，构成了一个无环图。

#### 2.1.2 DAG在数据结构中的作用
DAG在计算机科学和数据结构中有着多方面的应用。它能够表示元素之间的复杂关系，如任务调度、网页结构、社交网络等。在数据结构中，DAG作为基础概念，支持了诸如拓扑排序、最短路径等算法的实现。此外，DAG还能有效地表示和处理事务依赖，如在分布式计算、版本控制系统等场景中的应用。

### 2.2 拓扑排序算法解析

#### 2.2.1 拓扑排序的步骤与过程
拓扑排序是针对DAG的一种排序算法，它的目的是将DAG中的所有顶点排成一个线性序列，使得对于每一条有向边(u, v)，顶点u都在顶点v之前。拓扑排序的步骤通常包括：

1. 计算每个顶点的入度（即有多少条边指向该顶点）。
2. 将所有入度为0的顶点加入到排序结果中，并移除这些顶点以及它们的所有出边。
3. 重复步骤2，直到所有顶点都被移除或判断图中存在环。
4. 如果图中顶点全部移除，则存在拓扑排序；如果存在未被移除的顶点，则图中存在环，不可排序。

该过程可以用伪代码表示如下：

function topologicalSort(G):
    for each vertex in G:
        inDegree[vertex] ← 0
    for each edge (u, v) in G.edges:
        inDegree[v] ← inDegree[v] + 1

    L ← Empty list that will contain the sorted elements
    S ← Set of all nodes with no incoming edges

    while S is non-empty do:
        remove a vertex n from S
        add n to tail of L
        for each edge (n, m) in G do:
            if inDegree[m] - 1 == 0:
                insert m into S

    if L.length != |G|:
        return error // Graph has at least one cycle
    else:
        return L

#### 2.2.2 算法的时间复杂度分析
拓扑排序的时间复杂度主要由入度的计算和排序过程决定。入度的计算需要遍历所有边，对于每条边进行一次操作，其时间复杂度为O(E)，其中E为边的数量。排序过程涉及一个循环，每次循环移除一个顶点，直到所有顶点被移除或图中存在环，因此在最坏情况下，该过程的时间复杂度为O(V+E)，其中V为顶点的数量。

### 2.3 拓扑排序的数学模型

#### 2.3.1 线性规划与拓扑排序
线性规划是研究线性不等式或线性等式约束下的优化问题。在拓扑排序中，可以利用线性规划的理论来描述和求解某些特殊的排序问题。例如，可以将每个顶点的排序位置看作一个决策变量，并根据有向边的依赖关系建立相应的约束条件。

#### 2.3.2 图论中的相关定理和推导
在图论中，关于DAG和拓扑排序有许多重要的定理和推导。例如，一个DAG至少有一个拓扑排序，这是基于图中没有环的特性。此外，Kahn算法是一种基于拓扑排序的算法，可以在线性时间内对任何DAG进行排序。Kahn算法使用入度的计算和队列来记录入度为0的顶点，逐步构建出一个拓扑排序。

到此，我们已经探讨了拓扑排序的原理及其基本算法。在下一章中，我们将深入了解如何通过编程实现拓扑排序，并分析其在实际应用中的案例。

# 3. 拓扑排序的实践操作

在掌握了拓扑排序的基础理论和数学模型后，实践中如何具体实现拓扑排序成为一个关键问题。实践操作是将理论知识转化为可应用工具的桥梁，能够帮助开发者在面对实际问题时，更有效地利用拓扑排序解决复杂依赖关系。

## 3.1 编程实现拓扑排序

在编程实现拓扑排序的过程中，选择合适的编程语言是关键的第一步。不同的语言提供了不同的库和框架，能以不同的方式实现拓扑排序。

### 3.1.1 选择合适的编程语言

拓扑排序的算法实现可以使用多种编程语言，包括但不限于 Java、Python、C++ 等。每种语言都有自己的优势和局限性。在选择编程语言时，需要考虑算法的执行效率、开发效率、资源占用、可维护性以及应用场景。

- **Python**：因为其简洁的语法和丰富的数据结构，Python 成为初学者首选的语言。对于拓扑排序这种算法，Python 的代码实现简单直观，同时也有良好的性能。
- **Java**：Java 语言在企业应用中较为普遍，特别是对于大型系统。Java 的强类型系统和对象导向特性使得它在维护大型代码库时更加方便。
- **C++**：C++ 提供了接近硬件层面的操作能力，对于性能要求极高的场景，C++ 是一个很好的选择。然而，由于其相对复杂的语法，开发和维护难度较大。

在此，我们选择 Python 作为示例，因为它在算法教学和快速原型开发中有着广泛的使用。

### 3.1.2 核心算法的编码实现

实现拓扑排序的核心在于图的表示和遍历。以下是一个简单的 Python 示例，展示了如何使用邻接表表示图，并实现拓扑排序算法。

from collections import deque

def topological_sort(graph):
    # 计算每个节点的入度
    in_degree = {key: 0 for key in graph}
    for key in graph:
        for neighbour in graph[key]:
            in_degree[neighbour] += 1
    # 将所有入度为0的节点加入到队列中
    zero_in_degree_queue = deque([k for k in in_degree if in_degree[k] == 0])
    sorted_list = []  # 存储排序结果
    while zero_in_degree_queue:
        # 取出一个入度为0的节点
        current = zero_in_degree_queue.popleft()
        sorted