【DAG应用全解】：拓扑排序在有向无环图中的深入解析

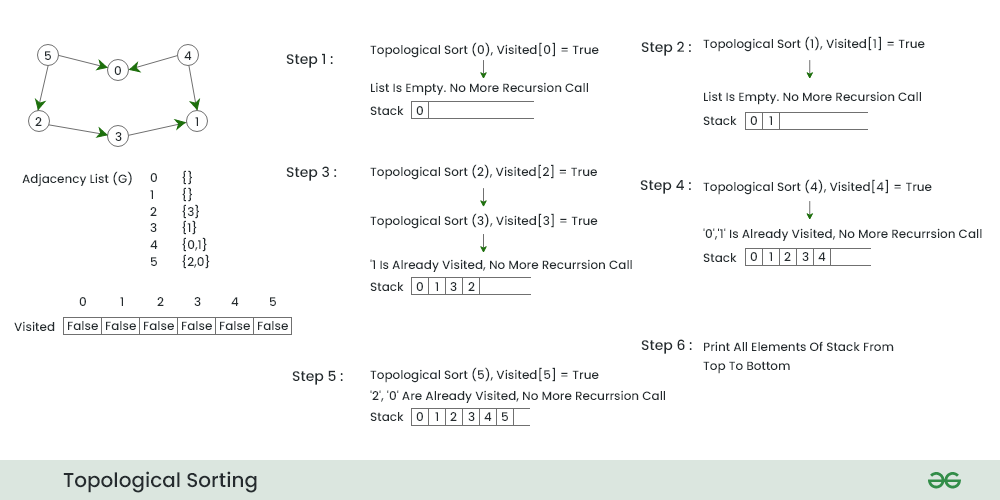
# 1. 有向无环图（DAG）基础概念

在计算机科学中，有向无环图（DAG）是图论中的一个重要概念。DAG由一组顶点（节点）和有方向的边组成，其中边从一个节点指向另一个节点。重要的是，DAG中不存在从一个节点出发，经过若干条边后又回到该节点的路径，这就是所谓的“无环”特性。DAG在许多领域都有广泛的应用，如数据处理、工作流管理、网络拓扑等。

## 1.1 DAG的基本组成元素

DAG由顶点（或节点）和有向边组成。每个节点可能具有多个输入边和多个输出边。在DAG中：

- 节点通常表示事件或任务。
- 有向边则表示节点间的依赖关系。

例如，在工作流中，节点可以代表特定的任务，而边则表示任务间的先后顺序。

## 1.2 DAG与其它图类型的对比

相较于无向图，DAG在表示依赖关系方面更为清晰和灵活。在有向图中，如果存在反向路径，则称其为循环依赖图，这在实际应用中往往需要避免，因为循环依赖会导致任务无法执行。DAG的无环特性使它在表示复杂关系的同时，能够保证任务的有序执行。

通过这一章的介绍，读者应当对DAG有了初步的理解。这将为接下来章节中对DAG的深入讨论和应用案例分析打下坚实的基础。

# 2. DAG的拓扑排序理论

## 2.1 拓扑排序的定义与重要性

### 2.1.1 拓扑排序的数学定义

拓扑排序是针对有向无环图（DAG）的一种排序方法，它将图中的所有顶点排成一个线性序列，使得对于图中的每一条有向边(u, v)，顶点u都排在顶点v之前。这个过程实际上是在对图中的节点进行排序，以确保每个节点在没有完成其所有先决条件任务之前不会被处理。在拓扑排序中，没有环的存在保证了图的每个节点最终都能被访问到，这在很多现实世界的应用中是一个重要的性质，比如任务调度、软件构建、课程表安排等。

### 2.1.2 拓扑排序在项目管理中的应用

在项目管理中，拓扑排序提供了一种方法来确定任务之间的依赖关系，并按照特定的顺序安排这些任务。例如，在软件开发中，各个模块可能相互依赖，开发者需要先编写和测试基础模块，然后才能开始依赖于这些模块的上层模块。拓扑排序能够帮助项目经理或者自动化构建系统创建一个可行的任务执行计划，确保所有依赖项在所需模块被处理前得到满足。通过这种方式，拓扑排序在减少工作流中的混乱和延误方面扮演着关键角色。

## 2.2 拓扑排序算法原理

### 2.2.1 算法思想与步骤概述

拓扑排序算法通常使用深度优先搜索（DFS）或者入度（in-degree）的概念。基于DFS的拓扑排序算法会从图中选择一个无前驱（即入度为0）的节点，访问这个节点，然后递归地对该节点的每个后继节点执行相同的操作。这种算法的关键在于，它能够确保在任何时候，都可以访问到一个没有前驱的节点，并进行处理。

另一种常见的方法是基于入度的处理，它会从图中移除入度为0的节点，并更新相邻节点的入度，重复这个过程直到所有的节点都被处理完毕。如果在处理过程中发现有节点的入度永远不能变为0，这意味着存在环，算法应当返回错误。

### 2.2.2 拓扑排序与图的遍历方法

在对DAG进行拓扑排序时，有几种图的遍历方法可以应用。最常见的方法之一是使用Kahn算法，它使用了队列来维护所有入度为0的节点。具体步骤如下：

1. 找出所有入度为0的节点，并将它们放入队列中。
2. 当队列不为空时，进行以下操作：
- 从队列中移除一个节点。
- 将该节点添加到排序结果中。
- 遍历该节点的所有后继节点，将其入度减1，并检查新的入度是否为0：
- 如果为0，则将其加入队列。
3. 重复上述步骤直到队列为空。如果排序结果中节点的个数与图中节点总数相同，则排序成功；否则，图中存在环。

Kahn算法提供了一种有效的解决方案，以确定节点处理的顺序，它基于队列的先进先出（FIFO）特性，能够有效地找出没有前驱依赖的节点，并确保依赖关系被正确处理。

## 2.3 拓扑排序的算法复杂度分析

### 2.3.1 时间复杂度分析

无论是基于DFS的拓扑排序算法还是基于入度的方法，时间复杂度分析都与图的表示方式密切相关。以邻接表为例，假设图中有V个顶点和E条边：

- DFS方法的时间复杂度为O(V+E)，因为它需要访问每个顶点一次，并且沿着每个边走一次。
- 基于入度的方法，比如Kahn算法，其时间复杂度也是O(V+E)。这是因为算法需要遍历所有顶点和边，以初始化入度并构建队列。

### 2.3.2 空间复杂度分析

空间复杂度主要取决于存储图所需的数据结构。在邻接表的实现中：

- 每个顶点都需要一个列表来存储它的所有后继节点，因此空间复杂度为O(V+E)。
- 此外，需要额外的空间来存储每个顶点的入度计数，这需要O(V)的空间。

综上所述，对于拓扑排序算法，空间复杂度主要受到图的规模影响，即顶点和边的数量。

在下一节中，我们将介绍具体的拓扑排序实现方法，包括使用邻接表和邻接矩阵的方式，并通过代码示例来进一步阐释这些算法的实现细节。

# 3. DAG拓扑排序的实现方式

## 3.1 基于邻接表的实现方法

### 3.1.1 邻接表的数据结构设计

在计算机科学中，邻接表是表示图的一种数据结构，它由一系列顶点的列表组成，每个顶点的列表包含所有与该顶点相邻的顶点。在实现DAG的拓扑排序时，使用邻接表可以有效地表示图中的依赖关系。

邻接表通常包含两个主要部分：
- 顶点表：存储图中所有的顶点，每个顶点都有一个唯一的标识。
- 边表：每个顶点对应一个边表，该边表包含了从该顶点出发到达的所有其他顶点。

为了实现拓扑排序，我们还需要记录每个顶点的入度（即有多少边指向该顶点）。初始时，入度为零的顶点被加入到一个队列中，作为排序的起始点。

### 3.1.2 具体实现代码解析

以下是一个使用Python实现的基于邻接表的拓扑排序算法代码段：

from collections import defaultdict, deque

# 构建邻接表表示的图
def build_graph(edges):
    graph = defaultdict(list)
    indegree = defaultdict(int)
    for u, v in edges:
        graph[u].append(v)
        indegree[v] += 1
    return graph, indegree

# 拓扑排序函数
def topological_sort(graph, indegree):
    zero_indegree_nodes = deque()
    for node in indegree:
        if indegree[node] == 0:
            zero_indegree_nodes.append(node)

    sorted_list = []
    while zero_indegree_nodes:
        current_node = zero_indegree_nodes.popleft()
        sorted_list.append(current_node)
        for neighbor in graph[current_node]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                zero_indegree_nodes.append(neighbor)
    if len(sorted_list) == len(graph):
        return sorted_list
    else:
        return None  # 存在环，无法进行拓扑排序

# 示例
edges = [('a', 'b'), ('a', 'c'), ('b', 'd'), ('c', 'd')]
graph, indegree = build_graph(edges)
sorted_result = topological_sort(graph, indegree)
print(sorted_result)

### 代码逻辑的逐行解读分析

- `build_graph` 函数接收一个边的列表，构建邻接表表示的图，并计算每个顶点的入度。
- `topological_sort` 函数实现了拓扑排序算法，首先找到所有入度为零的节点并加入队列。
- 接着，算法从队列中取出顶点，将其加入排序列表，并递归地将该顶点的所有邻接点的入度减一。
- 如果一个邻接点的入度减为零，则将其加入队列。
- 算法持续执行直到队列为空或者所有顶点都被处理。
- 如果排序完成后的列表长度与图的顶点数量相同，说明成功完成排序；否则，图中存在环，拓扑排序失败。

## 3.2 基于邻接矩阵的实现方法

### 3.2.1 邻接矩阵的数据结构设计

邻接矩阵是另一种图的表示方法，通过二维数组存储图中顶点之间的连接关系。在邻接矩阵中，矩阵的行和列都对应图中的顶点，如果顶点i和顶点j之间有边，则矩阵的[i][j]位置上为1，否则为0。

邻接矩阵特别适合表示稠密图，也就是图中边的数量接近顶点数平方的图。在拓扑排序中，我们同样需要记录每个顶点的入度，可以通过计算邻接矩阵的每一行之和来得到。

### 3.2.2 具体实现代码解析

以下是基于邻接矩阵的拓扑排序算法的Python代码实现：