【Python实践】：拓扑排序算法的简单实现

# 1. Python拓扑排序概述

拓扑排序是图论中的一项基础算法，它能够将有向无环图（DAG）中的节点线性排序，以体现节点间的依赖关系。在计算机科学中，这种排序特别适用于解决依赖和优先级问题，例如在编译器设计、项目管理和数据库等领域中。Python语言因其简洁性和强大的库支持，在处理这类算法问题时尤为突出。本章将从概念上简要介绍拓扑排序，并概述在Python中实现这一算法的基本思路。尽管我们在后续章节中将详细探讨算法的理论基础和具体实现，本章的目的是为读者提供一个关于Python中拓扑排序概念的快速概览。

# 2. 拓扑排序理论基础

### 2.1 图的介绍和分类

#### 2.1.1 无向图和有向图的区别

在图论中，图是一种由顶点(节点)和连接顶点的边组成的抽象数据结构。图可以被进一步分类为无向图和有向图。无向图中的边没有方向，表示顶点之间相互连接，而有向图中的边是有方向的，表示信息、物体、或控制从一个顶点流向另一个顶点。

**无向图**中的边可以简单看作是两个城市之间的双向道路，既可以从城市A到城市B，也可以从城市B到城市A。而在**有向图**中，边则像一个单行道，必须按照箭头指示的方向行驶，不能逆向。

例如，在社交网络图中，无向图可能用来表示两个用户之间的关系是双向的，可以互为朋友；而在表示网页链接结构时，有向图用来描述一个页面可以链接到另一个页面，但反过来不一定是。

#### 2.1.2 图的表示方法（邻接矩阵、邻接表）

图的表示方法是算法实现前必须考虑的一个重要方面。常见的图表示方法主要有邻接矩阵和邻接表。

**邻接矩阵**是一种二维数组表示方法，其中行和列分别代表图中的顶点。如果顶点i和顶点j之间有连接，则矩阵中对应位置M[i][j]为1，否则为0。邻接矩阵的优点是简单直观，但其空间复杂度较高，对于稀疏图不适用。

例如，对于一个有4个顶点的无向图：
  A B C D
A 0 1 0 0
B 1 0 1 0
C 0 1 0 1
D 0 0 1 0

**邻接表**用链表来表示顶点间的连接关系，每个顶点都有一个与其相连的顶点列表。邻接表节省空间，适合表示稀疏图，但需要额外的数据结构。

例如，对于同样的图，邻接表表示如下：
A -> B -> C
B -> A -> C
C -> B -> D
D -> C

邻接表和邻接矩阵的选择取决于图的稠密程度、查询和更新的需求等因素。

### 2.2 拓扑排序的定义和重要性

#### 2.2.1 拓扑排序的定义

拓扑排序是一种对有向无环图（DAG）的顶点进行排序的方法，使得对于任意的边(u, v)，顶点u都在顶点v之前。这种排序不是唯一的，但可以为我们提供一个有关顶点依赖关系的顺序。

拓扑排序的一个关键特性是它能够帮助我们发现和处理有向图中的环结构。由于拓扑排序只能应用于有向无环图，因此，在尝试进行拓扑排序之前，需要确认图中不存在环。

#### 2.2.2 拓扑排序的应用场景

拓扑排序在多个领域中有广泛应用，如课程安排、任务调度、软件包管理、编译器中的依赖解析等。

在课程安排系统中，课程依赖可以由图表示，其中节点代表课程，有向边表示课程的先修关系。拓扑排序可以用来生成满足先决条件的课程学习顺序。

在软件包管理中，包之间的依赖关系也形成一个有向图，通过拓扑排序，可以确定安装或更新软件包的顺序，以满足依赖关系。

### 2.3 拓扑排序的算法原理

#### 2.3.1 拓扑排序的Kahn算法原理

Kahn算法是进行拓扑排序的一种经典算法，其基本思想是每次移除一个入度为0的顶点，并将其邻接顶点的入度减1，如此迭代直到图中没有入度为0的顶点，此时如果图中还有剩余顶点，则表示图中存在环。

算法步骤如下：
1. 计算每个顶点的入度（指向该顶点的边的数量）。
2. 将所有入度为0的顶点加入队列中。
3. 当队列非空时，执行以下操作：
a. 从队列中取出一个顶点u。
b. 对u的所有邻接顶点v，将v的入度减1，如果v的入度变为0，则将其加入队列。
4. 如果图中所有顶点都被访问过，则完成拓扑排序，否则图中存在环。

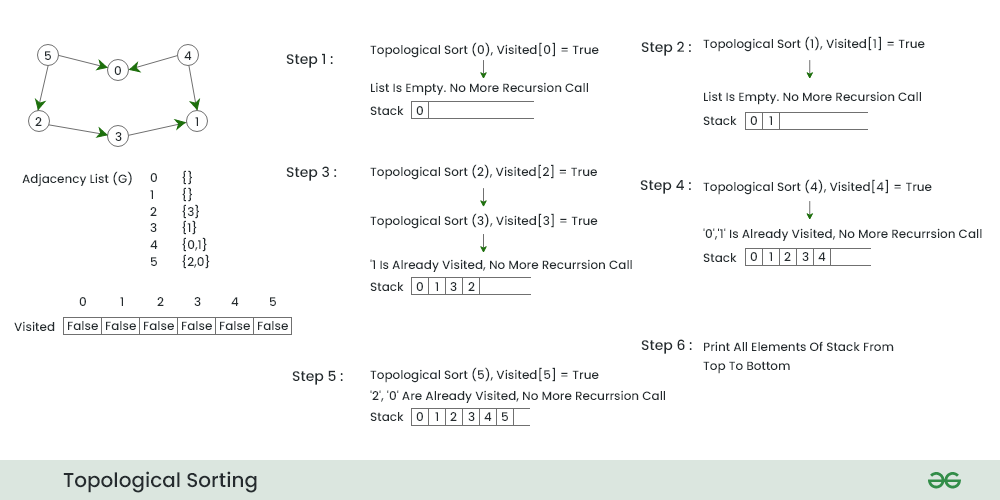
#### 2.3.2 拓扑排序的DFS算法原理

深度优先搜索（DFS）也可以用来进行拓扑排序。与Kahn算法不同的是，DFS算法从任意顶点开始，尽可能深地进行搜索，回溯时记录顶点的访问顺序，即为拓扑排序。

算法步骤如下：
1. 初始化一个空栈，用于存放拓扑排序结果。
2. 对所有未访问的顶点调用递归函数：
a. 对当前顶点标记为已访问。
b. 遍历当前顶点的所有邻接顶点，如果邻接顶点未被访问，则递归访问。
c. 当前顶点的所有邻接顶点都被访问过后，将其压入栈中。
3. 栈顶元素即为拓扑排序的开始，栈底元素为结束。

DFS算法在实现时需要注意避免对环结构中的顶点进行重复访问。在许多实现中，DFS用于检测图中的环并进行拓扑排序。

以上就是对拓扑排序理论基础的详细讲解，为接下来的Python实现部分打下坚实的理论基础。在下一章节中，我们将详细介绍如何使用Python语言实现拓扑排序，并结合实例演示其具体操作步骤。

# 3. Python实现拓扑排序

## 3.1 环境搭建与基础代码框架

### 3.1.1 搭建Python开发环境

在开始实现拓扑排序之前，确保您的开发环境已经搭建好Python的运行环境。推荐安装Python 3.x版本。您可以在官方文档找到详细安装指南。

此外，为了方便代码的编写和执行，您可以选择一些集成开发环境(IDE)，如PyCharm，或者使用文本编辑器配合命令行工具。

### 3.1.2 编写基础的数据结构代码

拓扑排序通常是在有向无环图(DAG)上进行的，所以我们首先需要定义图的数据结构。图可以通过邻接矩阵或邻接表表示。

class Graph:
    def __init__(self, vertices):
        self.graph = [[0] * vertices for _ in range(vertices)]
        self.V = vertices

    def add_edge(self, u, v):
        self.graph[u][v] = 1

    def print_graph(self):
        for i in range(self.V):
            for j in range(self.V):
                print(self.graph[i][j], end=" ")
            print()

# 示例用图的创建
g = Graph(6)
g.add_edge(5, 2)
g.add_edge(5, 0)
g.add_edge(4, 0)
g.add_edge(4, 1)
g.add_edge(2, 3)
g.add_edge(3, 1)

g.print_graph()

以上代码定义了一个有向图，并加入了几个边。这个基础图将用于后续的拓扑排序实现。

## 3.2 利用Kahn算法实现拓扑排序

### 3.2.1 Kahn算法的Python实现步骤

Kahn算法是进行拓扑排序的一种方法，它从没有入边（in-degree为0）的顶点开始，并逐步删除这些顶