【服务调度系统】：如何构建拓扑排序驱动的系统架构

# 1. 服务调度系统概述与核心概念

在现代IT行业中，服务调度系统已经成为构建高度可靠与动态扩展的分布式系统不可或缺的核心组件。该系统主要负责高效地管理、协调和执行任务，以确保服务的稳定性和性能。理解服务调度系统的基础概念，是深入探讨其设计、实现和优化的前提。

## 服务调度系统简介
服务调度系统是一种高度复杂的软件框架，它依据特定的调度策略和业务逻辑，合理分配计算资源，确保任务按照既定顺序和方式执行。这种系统通常涉及到任务队列管理、资源分配、负载均衡和故障恢复等多个方面。

## 核心组成要素
服务调度系统的基本组成包括任务调度器、资源管理器、执行器和调度策略。任务调度器负责处理任务的优先级、依赖关系和执行逻辑，资源管理器负责系统资源的分配和回收，执行器则是实际执行任务的组件。调度策略则是决定如何分配任务到执行器的决策机制。

## 服务调度的重要性
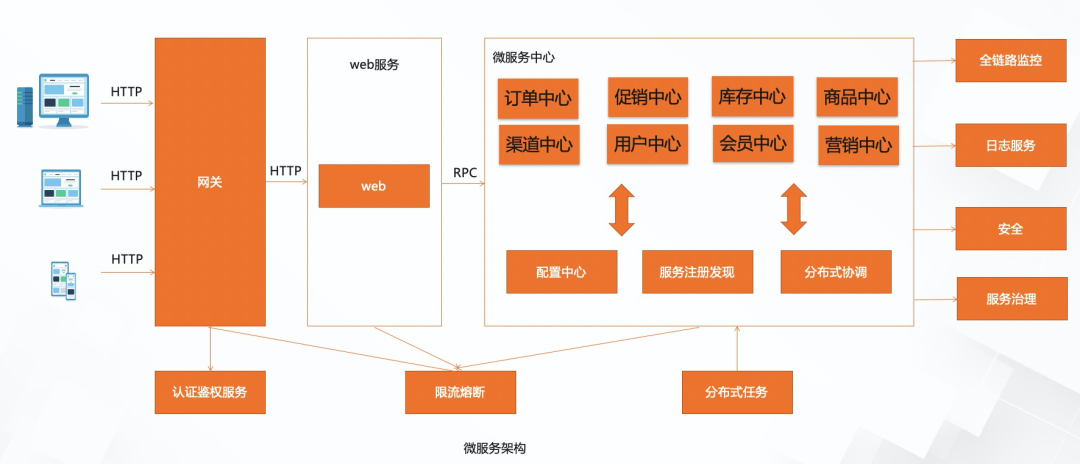
随着微服务架构和云计算的发展，服务调度在保证业务连续性、提高系统吞吐量、实现资源的高效利用等方面扮演着越来越重要的角色。它不仅能够优化任务执行效率，还能在面对系统故障时提供自动恢复的能力，是现代企业IT基础设施的重要组成部分。

# 2. 拓扑排序理论基础与实现

## 2.1 拓扑排序的基本原理

### 2.1.1 有向无环图与拓扑排序
在计算机科学和数学领域，有向无环图（Directed Acyclic Graph，简称DAG）是一种包含有向边且不包含环的图结构。在服务调度系统中，一个常见的应用场景是需要处理多个服务之间的依赖关系。服务之间的依赖关系可以自然地用有向无环图来表示，其中节点代表服务，边代表服务间的依赖关系。

拓扑排序是针对有向无环图的一种排序方式，它会返回一个线性序列，这个序列中的每个服务都排在它所依赖的服务之后。这种排序对于理解服务启动顺序至关重要。

### 2.1.2 拓扑排序算法解析
拓扑排序的算法实现通常涉及到以下几个步骤：

1. 首先，找到所有入度为0的节点，即没有依赖其他节点的节点。
2. 然后，将这些入度为0的节点加入到结果列表中，并从图中移除这些节点以及它们所指向的节点。
3. 更新图中剩余节点的入度值，重复步骤1和步骤2，直到图中没有节点或者剩余节点均无法从当前节点到达（即所有节点都被访问过）。
4. 如果有节点未能从图中移除，表明图中存在环，此时图不是DAG，无法进行拓扑排序。

接下来，将详细探讨如何实现拓扑排序算法，并应用到服务调度系统中。

## 2.2 拓扑排序的算法实践

### 2.2.1 实现步骤与代码示例
以Python语言为例，实现一个简单的拓扑排序算法。考虑到代码的可读性与扩展性，将使用字典来存储图数据。

def topological_sort(graph):
    # 1. 计算所有节点的入度
    indegree = {key: 0 for key in graph}
    for node in graph:
        for neighbor in graph[node]:
            indegree[neighbor] += 1
    # 2. 找出所有入度为0的节点，并构建入度为0的节点队列
    queue = [node for node in graph if indegree[node] == 0]
    # 3. 开始执行拓扑排序
    sorted_list = []
    while queue:
        node = queue.pop(0)
        sorted_list.append(node)
        for neighbor in graph[node]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                queue.append(neighbor)
    # 4. 检查是否所有的节点都被排序
    if len(sorted_list) == len(graph):
        return sorted_list
    else:
        raise Exception("图中存在环，无法进行拓扑排序")

该代码首先计算所有节点的入度值，然后创建一个队列来存储入度为0的节点。通过一个循环，不断从队列中取出节点，并将其加入到排序结果列表中。同时，更新相邻节点的入度值。如果所有节点都被访问过，则返回排序结果；否则，说明图中存在环。

### 2.2.2 算法的时间复杂度分析
上述拓扑排序算法的时间复杂度为O(V + E)，其中V是节点的数量，E是边的数量。这是因为算法需要遍历所有的节点和边来计算入度值，以及后续的排序过程中对节点的访问。因此，对于稀疏图来说，这是一个相当高效的算法。

## 2.3 拓扑排序在服务调度中的应用

### 2.3.1 服务依赖的拓扑表示
服务调度系统需要处理服务之间的依赖关系。通过拓扑排序，我们可以将服务依赖关系表示为一个有向无环图（DAG），并以拓扑顺序来确定服务启动的顺序。

### 2.3.2 拓扑排序与服务启动顺序
一旦服务依赖关系被转换为DAG，并且应用了拓扑排序，服务调度系统就可以根据排序结果来启动服务。通常情况下，服务依赖越多，它的启动顺序就越靠后。这样，服务调度系统可以确保在启动服务A之前，所有A依赖的服务都已经启动完毕。

下面是一个使用mermaid流程图来表示服务依赖和启动顺序的简单示例：

graph TD;
    S1-->|依赖|S2;
    S2-->|依赖|S3;
    S3-->|依赖|S4;
    S1[服务1];
    S2[服务2];
    S3[服务3];
    S4[服务4];

从上面的流程图中可以清晰地看出服务启动的依赖关系，因此拓扑排序在服务调度中的作用十分关键。

以上内容详细地解释了拓扑排序在理论与实践中的应用，从基本原理到具体算法实现，再到其在服务调度系统中的实际应用，通过代码和图表等形式，展示了其核心内容和实现细节。在下一章节中，我们将进一步深入探讨服务调度系统的设计与架构，展示如何将这些理论知识应用于构建稳定高效的服务调度系统。

# 3. 服务调度系统设计与架构

## 3.1 系统设计原则与框架选型

服务调度系统的设计旨在确保服务的高效、可靠和灵活的调度。这需要考虑一系列设计原则和选择合适的框架来支持这些原则。本节将探讨设计模式的应用和架构模式的选择，并通过