【时间复杂度杀手】：拓扑排序算法的优化秘诀

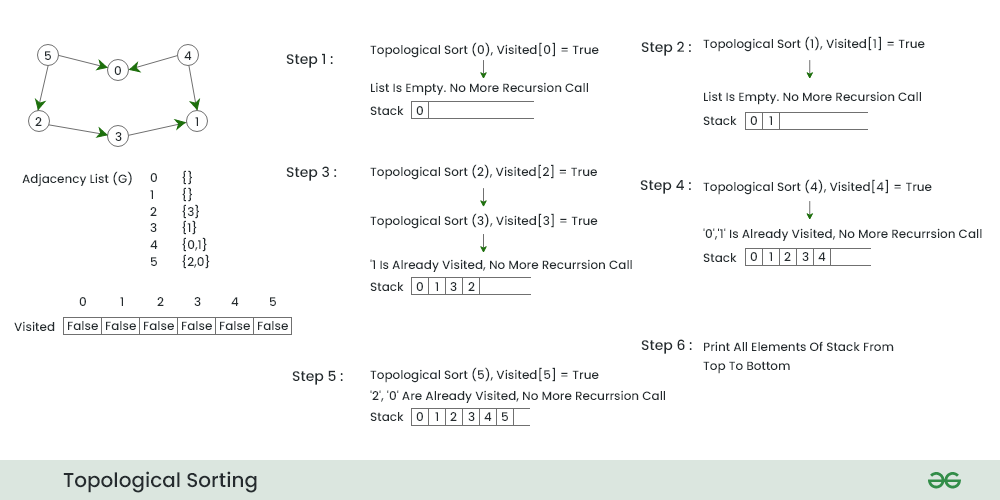
# 1. 拓扑排序算法简介

## 1.1 算法的基本概念

拓扑排序是计算机科学领域中对有向无环图（DAG）的一种排序方式。它是针对图的边进行排序，而不是顶点。其目的是，如果我们从图中的一个顶点开始，按照排序的结果遍历，每当我们到达一个顶点时，可以确保我们已经访问了该顶点的所有前驱顶点。在软件工程的构建系统、课程表设计、任务调度等多个领域都有广泛的应用。

## 1.2 算法的适用场景

拓扑排序算法适用于任何需要按照特定顺序处理元素的场景，其中元素之间存在依赖关系。例如，在软件开发过程中，编译和链接不同的库和模块时，可能需要按照依赖关系顺序进行。又如在进行课程表的编排时，需要确保课程按照先修课程的要求进行设置。

## 1.3 算法的基本步骤

执行拓扑排序的基本步骤如下：

1. 找到所有入度为0的顶点，并将它们放入队列中。
2. 当队列非空时，执行以下操作：
- 从队列中取出一个顶点，进行处理（例如打印）。
- 更新它的所有邻接顶点的入度（如果该顶点的邻接点入度减1后为0，则将其入队）。
3. 重复步骤2，直到队列为空。

这个过程可以使用队列数据结构高效实现，我们会通过代码示例在后续章节中深入探讨。拓扑排序算法保证了在一个DAG中，只有在所有的前驱节点被访问之后，节点才会被访问，这在处理具有依赖关系的数据或任务时非常有用。

# 2. 时间复杂度与拓扑排序

## 2.1 时间复杂度的基本概念

### 2.1.1 时间复杂度的定义

时间复杂度是衡量算法运行时间与输入大小之间关系的度量。它关注的是随着输入规模的增加，算法运行时间如何变化。我们使用大O符号来表示时间复杂度，如O(n)、O(n^2)等。它并不表示精确的时间长度，而是描述了算法效率的上界。一个O(n)的算法表示该算法的执行时间与输入大小n成线性关系。

### 2.1.2 常见的时间复杂度类

时间复杂度有很多种，它们代表了算法运行时间的不同增长速率。以下是几种常见的复杂度类别：

- O(1) - 常数时间复杂度：算法运行时间不依赖于输入大小。
- O(log n) - 对数时间复杂度：通常与二分查找相关。
- O(n) - 线性时间复杂度：算法执行时间与输入大小直接成正比。
- O(n log n) - 线性对数时间复杂度：常见于高效的排序算法，如快速排序。
- O(n^2) - 平方时间复杂度：常见于简单的排序和搜索算法，如冒泡排序。
- O(2^n) - 指数时间复杂度：与递归相关的算法。
- O(n!) - 阶乘时间复杂度：与穷举法相关。

## 2.2 拓扑排序算法的理论基础

### 2.2.1 有向无环图(DAG)与拓扑排序

拓扑排序是针对有向无环图（DAG）的一种排序算法，其目的是将图中的顶点线性排序，使得对于任意有向边(u, v)，顶点u都在顶点v之前。这种排序不是唯一的，它依赖于图的具体结构。拓扑排序的结果表明了任务的执行顺序，非常适合用于解决依赖关系问题。

### 2.2.2 拓扑排序的算法流程

拓扑排序的基本流程如下：

1. 找到所有入度为0的顶点，并将它们加入一个队列。
2. 当队列非空时，从队列中取出一个顶点，将其添加到排序结果中。
3. 对于该顶点的所有邻接顶点，将它们的入度减1（如果新的入度为0，则加入队列）。
4. 重复步骤2和3，直到队列为空。

## 2.3 拓扑排序算法的时间复杂度分析

### 2.3.1 标准拓扑排序的时间复杂度

标准拓扑排序算法的时间复杂度为O(V+E)，其中V是顶点的数量，E是边的数量。这是因为在执行拓扑排序时，每个顶点至多入队和出队一次，每条边至多被检查一次。因此，算法的总操作次数与顶点数和边数成线性关系。

### 2.3.2 时间复杂度对算法性能的影响

时间复杂度决定了算法在处理大数据集时的性能表现。对于拓扑排序来说，O(V+E)的时间复杂度意味着算法能够高效地处理大规模的DAG。然而，在图结构非常密集的情况下（即边的数量接近顶点数量平方），算法的性能会受到一定影响。在这种情况下，优化算法的具体实现就显得尤为重要。

# 3. 拓扑排序的常见实现方法

在数据结构与算法领域中，拓扑排序是一种针对有向无环图(DAG)的操作，用于确定图中节点的线性顺序，以反映它们之间的依赖关系。本章节将深入探讨拓扑排序的几种实现方式，包括使用队列和栈的基本实现，以及基于优先队列的优化实现。通过比较不同实现的原理、代码示例以及各自的优缺点，我们将对如何选择合适的实现方法有一个清晰的认识。

## 3.1 队列实现的拓扑排序

队列实现的拓扑排序是最直观的方法，其基本原理是使用一个队列来维护所有入度为零的节点，并通过不断地出队和更新节点的入度，来实现排序。

### 3.1.1 队列实现原理

队列实现的拓扑排序遵循以下步骤：

1. 找到所有入度为零的节点，将它们入队。
2. 当队列非空时，执行以下操作：
a. 从队列中取出一个节点。
b. 将该节点的邻接节点的入度减一。
c. 如果某个邻接节点的入度变为零，则将其入队。
3. 重复步骤2，直到队列为空。
4. 如果图中不存在入度为零的节点，但仍有节点未被访问，则说明图中存在环，无法进行拓扑排序。

### 3.1.2 队列实现的代码示例

以下是使用Python实现队列式拓扑排序的一个示例代码：

from collections import deque

def topological_sort(graph, num_vertices):
    in_degree = [0] * num_vertices
    queue = deque()
    sorted_order = []

    # Step 1: 计算所有节点的入度并找到所有入度为零的节点
    for i in range(num_vertices):
        for j in graph[i]:
            in_degree[j] += 1
    for i in range(num_vertices):
        if in_degree[i] == 0:
            queue.append(i)

    # Step 2: 执行队列操作
    while queue:
        node = queue.popleft()
        sorted_order.append(node)
        for adjacent in graph[node]:
            in_degree[adjacent] -= 1
            if in_degree[adjacent] == 0:
                queue.append(adjacent)

    # Step 3: 检查是否所有节点都被访问
    if len(sorted_order) != num_vertices:
        return None  # 图中存在环

    return sorted_order

# 示例使用
if __name__ == "__main__":
    num_vertices = 6
    graph = [[] for _ in range(num_vertices)]
    # 添加边信息构建DAG图
    graph[5].append(2)
    graph[5].append(0)
    graph[4].append(0)
    graph[4].append(1)
    graph[2].append(3)
    graph[3].append(1)

    sorted_order = topological_sort(graph, num_vertices)