混合滤波：多模型状态空间模型求解，3个应用场景

# 1. 混合滤波的基本原理**

混合滤波是一种融合多个模型或滤波器的技术，旨在提高估计精度和鲁棒性。其基本原理在于，不同的模型或滤波器可能在不同的条件或场景下表现出不同的优势，通过融合这些模型或滤波器的输出，可以获得更准确和稳健的估计结果。

混合滤波通常采用加权平均或概率密度融合等方法来融合不同模型或滤波器的输出。此外，混合滤波还涉及模型切换策略，例如概率切换或决策切换，以根据当前条件或场景选择最合适的模型或滤波器。

# 2. 多模型状态空间模型**

**2.1 模型融合方法**

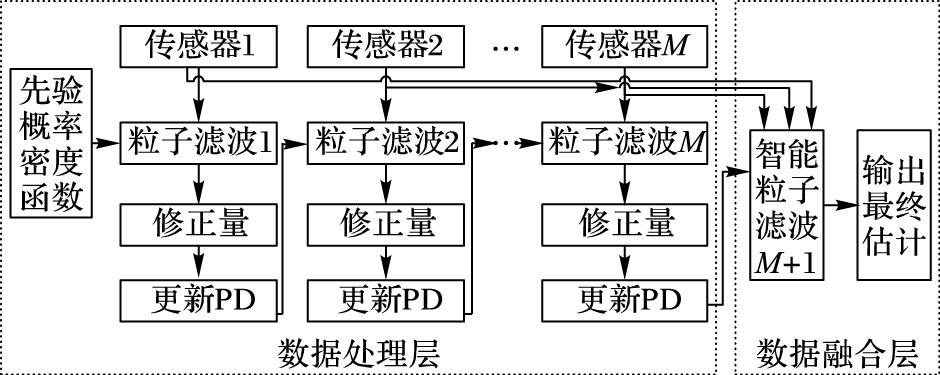
多模型状态空间模型融合了多个模型来描述一个动态系统，每个模型都捕捉系统的一个特定方面。融合方法将这些模型的输出结合起来，生成一个更准确和鲁棒的估计。

**2.1.1 加权平均融合**

加权平均融合是一种简单但有效的融合方法。它将每个模型的输出加权平均，权重由模型的置信度决定。置信度可以基于模型的过去性能或其他因素。

def weighted_average_fusion(models, weights):
    """加权平均融合
    Args:
        models: 模型列表
        weights: 权重列表
    Returns:
        融合后的输出
    """
    fused_output = 0
    for model, weight in zip(models, weights):
        fused_output += weight * model.output
    return fused_output

**2.1.2 概率密度融合**

概率密度融合是一种更复杂的融合方法，它考虑了每个模型输出的概率分布。它将这些分布融合成一个新的分布，该分布表示融合后的估计。

def probability_density_fusion(models):
    """概率密度融合
    Args:
        models: 模型列表
    Returns:
        融合后的概率分布
    """
    fused_distribution = None
    for model in models:
        if fused_distribution is None:
            fused_distribution = model.output.copy()
        else:
            fused_distribution += model.output
    return fused_distribution

**2.2 模型切换策略**

模型切换策略决定在不同时间步使用哪个模型。这可以通过概率或决策规则来实现。

**2.2.1 概率切换**

概率切换根据每个模型的置信度在模型之间切换。置信度可以基于模型的过去性能或其他因素。

def probability_switching(models, probabilities):
    """概率切换
    Args:
        models: 模型列表
        probabilities: 概率列表
    Returns:
        切换后的模型
    """
    chosen_model = None
    for model, probability in zip(models, probabilities):
        if random.random() < probability:
            chosen_model = model
    return chosen_model

**2.2.2 决策切换**

决策切换根据预定义的规则在模型之间切换。这些规则可以基于系统状态或其他因素。

def decision_switching(models, decision_rules):
    """决策切换
    Args:
        models: 模型列表
        decision_rules: 决策规则列表
    Returns:
        切换后的模型
    """
    chosen_model = None
    for model, decision_rule in zip(models, decision_rules):
        if decision_rule(system_state):
            chosen_model = model
    return chosen_model

# 3. 混合滤波的实践应用

### 3.1 目标跟踪

目标跟踪是混合滤波的一个重要应用领域。目标跟踪的目的是估计目标的状态（如位置、速度），即使目标受到噪声、遮挡和运动模糊等因素的影响。

#### 3.1.1 卡尔曼滤波

卡尔曼滤波是一种经典的线性滤波器，它可以估计目标的状态。卡尔曼滤波器通过预测和更新两个步骤来工作：

- **预测步骤：**预测目标的状态和协方差矩阵。
- **更新步骤：**使用测量值更新目标的状态和协方差矩阵。

**代码块：**

import numpy as np

class KalmanFilter:
    def __init__(self, A, B, H, Q, R):
        self.A = A  # 状态转移矩阵
        self.B = B  # 控制矩阵
        self.H = H  # 观测矩阵
        self.Q = Q  # 过程噪声协方差矩阵
        self.R = R  # 测量噪声协方差矩阵

    def predict(self, x, u):
        """预测状态和协方差矩阵。

        Args:
            x: 当前状态
            u: 控制输入
        """
        x = self.A @ x + self.B @ u
        P = self.A @ P @ self.A.T + self.Q

        return x, P

    def update(self, x, P, z):
        """更新状态和协方差矩阵。

        Args:
            x: 当前状态
            P: 当前协方差矩阵
            z: 测量值
        """
        K = P @ self.H.T @ np.linalg.inv(self.H @ P @ self.H.T + self.R)
        x = x + K @ (z - self.H @ x)
        P = (np.eye(len(x)) - K @ self.H) @ P

        return x, P

**逻辑分析：**

* `predict()` 函数使用状态转移矩阵 `A` 和控制输入 `u` 预测状态 `x` 和协方差矩阵 `P`。
* `update()` 函数使用观测矩阵 `H`、测量值 `z` 和卡尔曼增益 `K` 更新状态 `x` 和协方差矩阵 `P`。

#### 3.1.2 粒子滤波

粒子滤波是一种非参数滤波器，它可以估计目标的状态，即使状态空间是非线性的。粒子滤波器通过以下步骤工作：

- **初始化：**生成一组粒子，每个粒子代表目标状态的一个可能值。
- **预测：**使用状态转移模型预测每个粒子的状态。
- **权重更新：**根据测量值更新每个粒子的权重。
- **重采样：**重新生成一组粒子，其中权重较高的粒子更有可能被选择。

**代码块：**

import numpy as np
import random

class ParticleFilter:
    def __init__(self, n_particles, state_dim, transition_model, observation_model):
        self.n_particles = n_particles
        self.state_dim = state_dim
        self.transition_model = transition_model
        self.observation_model = observation_model

    def initialize(self):
        """初始化粒子。"""
        self.particles = np.random.rand(self.n_particles, self.state_dim)

    def predict(self):
        ""