平方根信息滤波：非线性状态空间模型求解，4个应用实例

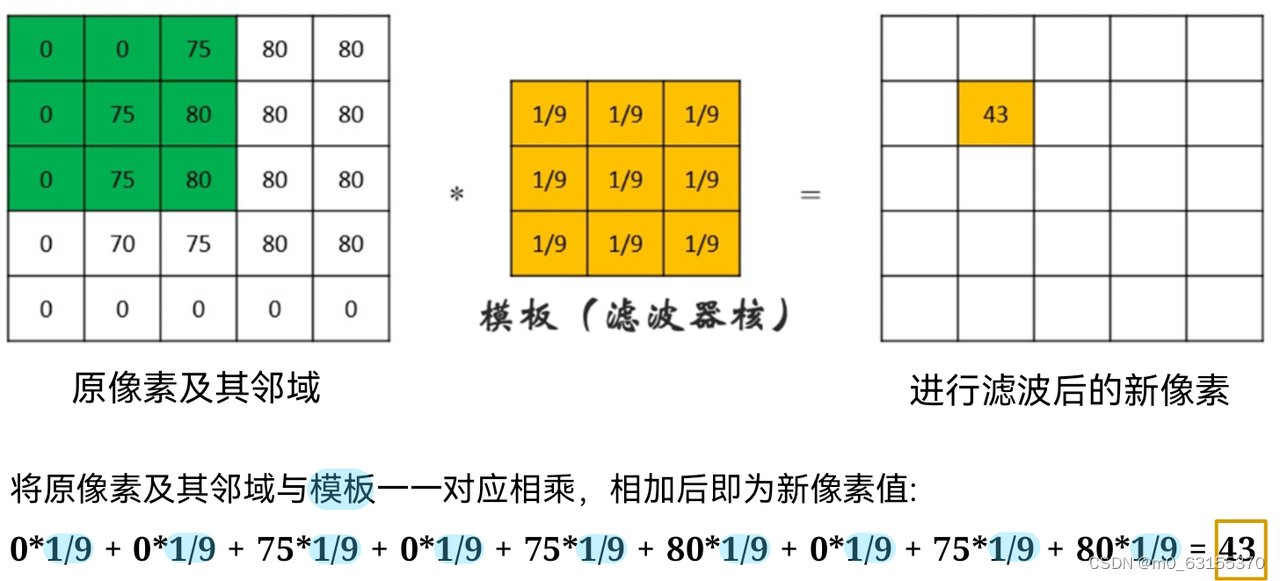
# 1. 平方根信息滤波简介

平方根信息滤波（SR-IF）是一种非线性状态估计算法，它在处理非线性状态空间模型时具有独特的优势。与卡尔曼滤波器不同，SR-IF通过对信息矩阵进行平方根分解来避免矩阵求逆运算，从而提高了计算效率。

SR-IF特别适用于处理高维、非线性的系统，例如机器人导航、目标跟踪和计算机视觉等领域。它能够有效地估计系统的状态和协方差，并对非线性测量和过程噪声具有鲁棒性。

# 2. 平方根信息滤波算法

### 2.1 理论基础

#### 2.1.1 非线性状态空间模型

平方根信息滤波算法适用于非线性状态空间模型，该模型由以下方程描述：

x[k] = f(x[k-1], u[k], w[k])
y[k] = h(x[k], v[k])

其中：

* `x[k]`：状态向量，表示系统在时刻 `k` 的状态
* `u[k]`：控制输入
* `w[k]`：过程噪声，假设为均值为 0，协方差矩阵为 `Q` 的高斯分布
* `y[k]`：观测向量，表示系统在时刻 `k` 的观测值
* `v[k]`：观测噪声，假设为均值为 0，协方差矩阵为 `R` 的高斯分布
* `f`：非线性状态转移函数
* `h`：非线性观测函数

#### 2.1.2 平方根信息滤波的推导

平方根信息滤波算法通过对协方差矩阵进行平方根分解来实现，从而避免了协方差矩阵的直接计算。其推导过程如下：

**预测步骤：**

P[k|k-1] = P[k-1|k-1] - P[k-1|k-1] F[k] P[k-1|k-1]

其中：

* `P[k|k-1]`：预测协方差矩阵
* `P[k-1|k-1]`：先验协方差矩阵
* `F[k]`：状态转移雅可比矩阵

**更新步骤：**

K[k] = P[k|k-1] H[k] (H[k] P[k|k-1] H[k] + R[k])^-1
x[k|k] = x[k|k-1] + K[k] (y[k] - h(x[k|k-1]))
P[k|k] = (I - K[k] H[k]) P[k|k-1]

其中：

* `K[k]`：卡尔曼增益
* `H[k]`：观测雅可比矩阵
* `R[k]`：观测噪声协方差矩阵
* `x[k|k]`：后验状态估计
* `P[k|k]`：后验协方差矩阵

### 2.2 实践实现

#### 2.2.1 算法流程

平方根信息滤波算法的流程图如下：

graph LR
subgraph 预测步骤
    A[预测]
    B[计算F]
    C[计算P]
end
subgraph 更新步骤
    D[计算H]
    E[计算K]
    F[更新x]
    G[更新P]
end
A --> B --> C
D --> E --> F --> G

#### 2.2.2 代码示例

以下代码展示了平方根信息滤波算法的 Python 实现：

import numpy as np

class SquareRootInformationFilter:
    def __init__(self, x0, P0, F, H, Q, R):
        self.x = x0
        self.P = P0
        self.F = F
        self.H = H
        self.Q = Q
        self.R = R