机器学习中的状态空间模型：4个应用场景，提升模型预测力

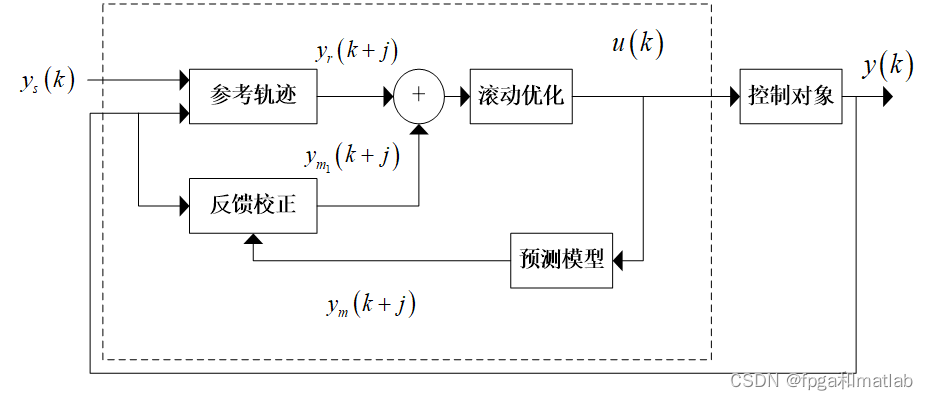
# 1. 状态空间模型概述

状态空间模型（SSM）是一种强大的统计建模框架，用于表示和预测动态系统。它将系统状态（不可直接观测）和观测值（可观测）联系起来，从而能够对系统行为进行推理和预测。

SSM由两个方程组成：状态方程描述系统状态随时间的变化，而观测方程描述观测值与系统状态之间的关系。通过使用这些方程，我们可以推断系统的隐藏状态，即使这些状态不可直接观测。

SSM广泛应用于各种领域，包括时间序列预测、动态系统估计、异常检测和优化控制。它们为理解和预测复杂系统提供了强大的工具，并在许多实际应用中取得了成功。

# 2. 状态空间模型的应用场景

状态空间模型在机器学习中具有广泛的应用场景，涵盖了预测、估计、检测和优化等多个领域。本章节将深入探讨状态空间模型在以下四个方面的应用：

### 2.1 预测时间序列数据

时间序列数据是按时间顺序排列的一系列观测值，通常具有趋势、季节性和随机性等特征。状态空间模型可以有效地捕捉这些特征，从而实现时间序列数据的预测。

**2.1.1 Kalman滤波**

Kalman滤波是一种线性状态空间模型，用于估计动态系统的状态。它通过递归更新状态和协方差矩阵，实现对时间序列数据的平滑估计。Kalman滤波在金融、工程和控制等领域得到了广泛应用。

**代码块：**

import numpy as np
from KalmanFilter import KalmanFilter

# 定义状态空间模型
A = np.array([[1, 1], [0, 1]])  # 状态转移矩阵
B = np.array([[0], [1]])  # 控制矩阵
C = np.array([[1, 0]])  # 观测矩阵
Q = np.array([[0.0001, 0], [0, 0.0001]])  # 状态噪声协方差矩阵
R = np.array([[0.01]])  # 观测噪声协方差矩阵

# 初始化Kalman滤波器
kf = KalmanFilter(A, B, C, Q, R)

# 观测数据
y = np.array([1, 2, 3, 4, 5])

# 预测和更新
for i in range(len(y)):
    kf.predict()
    kf.update(y[i])

# 获取估计状态
x_hat = kf.x

**逻辑分析：**

* 状态转移矩阵A表示状态在时间步长之间的变化。
* 控制矩阵B表示控制输入对状态的影响。
* 观测矩阵C表示状态与观测之间的关系。
* 状态噪声协方差矩阵Q表示状态转移过程中的不确定性。
* 观测噪声协方差矩阵R表示观测过程中的不确定性。
* predict()方法更新状态和协方差矩阵的先验估计。
* update()方法使用观测数据更新状态和协方差矩阵的后验估计。
* x_hat是估计的状态，它表示系统在当前时间步长下的最佳估计。

**2.1.2 粒子滤波**

粒子滤波是一种非线性状态空间模型，用于估计非线性动态系统的状态。它通过维护一组加权粒子来近似状态的后验分布。粒子滤波在目标跟踪、机器人导航和语音识别等领域得到了广泛应用。

**代码块：**

import nump