网络安全中的自组织映射（SOM）：识别威胁的隐形卫士

# 1. 网络安全威胁概览

网络安全威胁无处不在，对个人、组织和国家构成严重威胁。这些威胁不断演变，从传统的恶意软件到先进的网络攻击。了解这些威胁至关重要，以便制定有效的防御策略。

常见的网络安全威胁包括：

- **恶意软件：**病毒、蠕虫、木马和其他恶意软件可以破坏系统、窃取数据或执行其他恶意操作。
- **网络钓鱼：**网络犯罪分子伪装成合法实体发送电子邮件或消息，诱骗受害者泄露个人信息或访问恶意网站。
- **网络攻击：**黑客利用网络漏洞未经授权访问系统、窃取数据或破坏服务。
- **数据泄露：**未经授权访问敏感数据，例如财务信息、医疗记录或个人身份信息。
- **勒索软件：**恶意软件加密受害者的文件并要求支付赎金以解锁它们。

# 2. 自组织映射（SOM）理论基础**

## 2.1 SOM算法原理

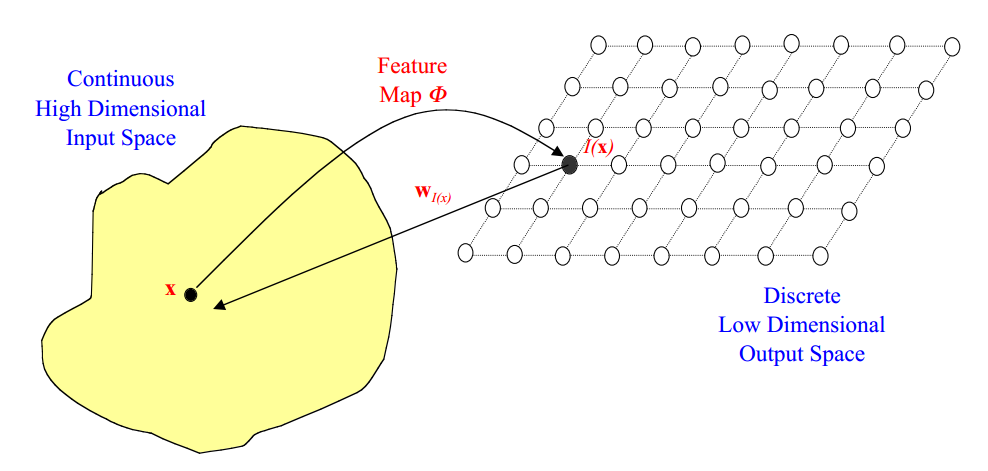
自组织映射（SOM）是一种无监督学习算法，旨在将高维数据映射到低维空间，同时保留输入数据的拓扑结构。SOM算法的核心思想是通过竞争学习机制和拓扑结构的更新来实现数据映射。

### 2.1.1 竞争学习机制

竞争学习机制是SOM算法的关键部分。在训练过程中，每个神经元与输入数据样本竞争，以确定哪个神经元与该样本最相似。相似度通常使用欧几里得距离或其他距离度量来计算。

获胜神经元及其邻域内的神经元将更新其权重，向输入样本移动。这种更新过程通过以下公式实现：

w_ij(t+1) = w_ij(t) + α(t) * (x_i(t) - w_ij(t))

其中：

* `w_ij(t)`：神经元`i`在时间`t`的权重
* `x_i(t)`：输入数据样本`i`在时间`t`的值
* `α(t)`：学习率，随着训练的进行而减小

### 2.1.2 拓扑结构和邻域函数

SOM算法使用一个二维拓扑结构，通常是一个网格或六边形网格。每个神经元都位于拓扑结构中的特定位置，并且与相邻的神经元相连。

邻域函数用于定义神经元的邻域，即受获胜神经元权重更新影响的神经元。邻域函数通常使用高斯函数或其他衰减函数，随着与获胜神经元的距离增加而减小。

## 2.2 SOM的优势和局限性

**优势：**

* **数据可视化：**SOM可以将高维数据映射到低维空间，从而实现数据的可视化。
* **拓扑保留：**SOM保留了输入数据的拓扑结构，使得相似的样本在映射后的空间中也相邻。
* **无监督学习：**SOM不需要标记数据进行训练，使其适用于各种网络安全应用。

**局限性：**

* **训练时间长：**SOM训练过程可能需要大量时间，尤其是对于大型数据集。
* **参数敏感：**SOM算法对参数（如学习率和邻域半径）很敏感，需要仔细调整以获得最佳性能。
* **维度限制：**SOM通常只能将数据映射到二维空间，这可能会限制其在某些应用中的使用。

# 3. SOM在网络安全中的应用

自组织映射（SOM）在网络安全领域具有广泛的应用，包括异常检测、攻击分类和威胁情报分析。

### 3.1 异常检测

异常检测是识别网络中偏离正常行为模式的活动。SOM通过将网络流量数据映射到低维空间，可以有效地检测异常。

**3.1.1 训练SOM模型**

SOM模型的训练过程如下：

1. **数据预处理：**对网络流量数据进行预处理，包括特征提取、归一化和降维。
2. **初始化：**随机初始化SOM网格的权重向量。
3. **竞争学习：**对于每个输入数据，找到最相似的权重向量并将其标记为获胜神经元。
4. **权重更新：**调整获胜神经元及其相邻神经元的权重，使其更接近输入数据。
5. **迭代：**重复步骤3和4，直到模型收敛或达到最大迭代次数。

**3.1.2 异常检测算法**

训练好的SOM模型可以用于检测异常：

1. **输入新数据：**将新网络流量数据输入SOM模型。
2. **计算距离：**计算新数据与每个权重向量的距离。
3. **识别异常：**具有最大距离的权重向量对应的区域被标记为异常。

### 3.2