金融领域的自组织映射（SOM）：揭示市场趋势的利器

# 1. 自组织映射（SOM）概述

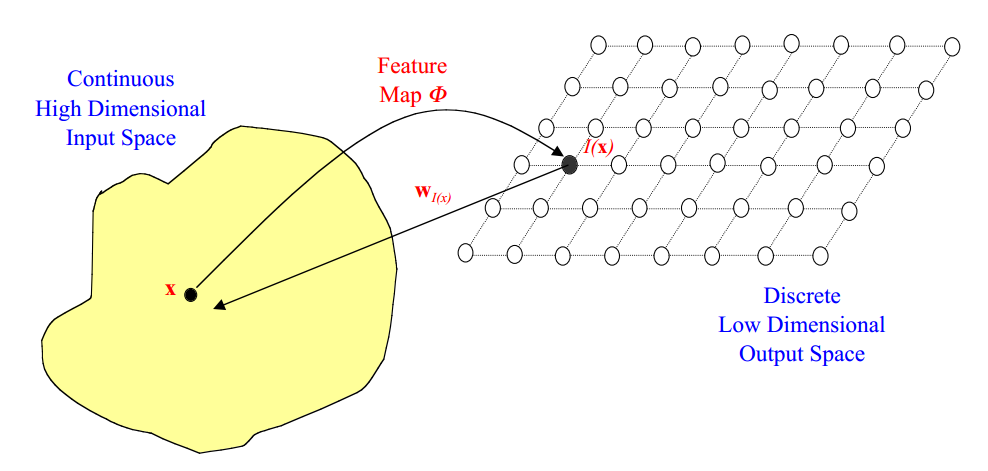
自组织映射（SOM）是一种无监督机器学习算法，能够将高维数据映射到低维空间中，同时保留输入数据的拓扑结构。它是一种神经网络，由一个由神经元组成的网格组成，每个神经元都与输入数据中的一个特征相关联。SOM通过竞争学习算法进行训练，其中神经元竞争以表示输入数据中的特定模式。训练后，SOM可以用于可视化和分析高维数据，识别模式和趋势，并进行预测。

# 2. SOM在金融领域的理论基础

### 2.1 SOM算法原理

自组织映射（SOM）是一种无监督机器学习算法，它将高维数据映射到低维空间（通常是二维或三维），同时保留输入数据的拓扑结构。SOM算法的主要步骤如下：

1. **初始化：**随机初始化一个与输出空间维度相同的权重矩阵。
2. **竞争：**对于每个输入数据，计算其与所有权重向量的距离，并选择距离最小的权重向量。
3. **合作：**对获胜权重向量及其邻近的权重向量进行更新，使其更接近输入数据。
4. **重复：**重复步骤2和3，直到达到预定的迭代次数或满足收敛条件。

### 2.2 SOM在金融领域的适用性

SOM算法在金融领域具有广泛的适用性，因为它能够处理高维、非线性和动态数据。具体而言，SOM在金融领域的适用性体现在以下几个方面：

- **数据降维：**SOM可以将高维金融数据（如股票价格、外汇汇率等）降维到低维空间，便于可视化和分析。
- **模式识别：**SOM可以识别金融数据中的模式和趋势，例如市场趋势、风险模式和投资机会。
- **非线性关系建模：**SOM可以捕捉金融数据中的非线性关系，这对于预测和风险管理至关重要。
- **动态数据处理：**SOM可以处理随着时间变化的金融数据，使其能够适应不断变化的市场环境。

**代码块：**

import numpy as np
import matplotlib.pyplot as plt

# 初始化权重矩阵
weights = np.random.rand(100, 2)

# 训练SOM
for i in range(1000):
    # 获取输入数据
    data = np.random.rand(100, 2)

    # 竞争
    distances = np.linalg.norm(data - weights, axis=1)
    winner = np.argmin(distances)

    # 合作
    radius = np.exp(-i / 1000)
    for j in range(100):
        distance = np.linalg.norm(j - winner)
        if distance < radius:
            weights[j] += radius * (data[i] - weights[j])

# 可视化SOM
plt.scatter(data[:, 0], data[:, 1])
plt.scatter(weights[:, 0], weights[:, 1], c='red')
plt.show()