图像处理中的自组织映射（SOM）：解锁图像分析新境界

# 1. 自组织映射（SOM）简介

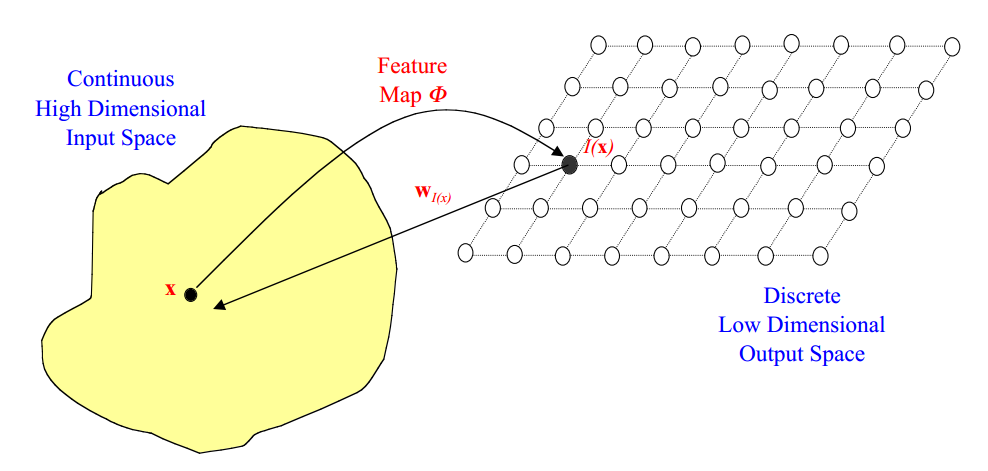
自组织映射（SOM）是一种非监督式神经网络算法，它能够将高维数据映射到低维空间中，同时保留输入数据的拓扑结构。SOM在图像处理、聚类和降维等领域有着广泛的应用。

SOM的结构类似于一个二维网格，每个神经元都具有一个权重向量。在训练过程中，SOM将输入数据映射到网格中，使得相似的输入数据被映射到相邻的神经元上。这种映射关系反映了输入数据的拓扑结构，从而可以用于图像聚类、降维和识别等任务。

# 2. SOM理论基础

### 2.1 SOM的神经网络模型

#### 2.1.1 SOM的结构和算法

自组织映射（SOM）是一种无监督神经网络，它通过自组织学习的过程将高维输入数据映射到低维输出空间中。SOM的结构类似于一个网格，其中每个节点（神经元）都与一个权重向量相关联。

SOM的算法如下：

1. **初始化：**随机初始化每个节点的权重向量。
2. **输入：**将输入数据呈现给SOM。
3. **最佳匹配单元（BMU）查找：**计算每个节点的权重向量与输入数据之间的距离，并找到距离最小的节点，称为最佳匹配单元（BMU）。
4. **权重更新：**更新BMU及其相邻节点的权重向量，使其更接近输入数据。
5. **重复：**重复步骤2-4，直到满足终止条件（例如，达到最大迭代次数或误差低于阈值）。

#### 2.1.2 SOM的学习过程

SOM的学习过程是一个自组织的过程，其中神经元通过竞争和合作来调整自己的权重向量。

* **竞争：**BMU及其相邻节点在更新权重向量时会竞争，以更好地表示输入数据。
* **合作：**BMU的相邻节点也会更新其权重向量，但幅度较小，这有助于形成拓扑结构，其中相邻节点表示相似的输入数据。

### 2.2 SOM的数学原理

#### 2.2.1 SOM的距离度量

SOM使用欧几里得距离或余弦相似度等距离度量来计算节点的权重向量与输入数据之间的距离。

#### 2.2.2 SOM的权重更新公式

BMU及其相邻节点的权重更新公式如下：

w_i(t+1) = w_i(t) + α(t) * (x(t) - w_i(t))

其中：

* `w_i(t)` 是第`i`个节点在时间`t`的权重向量。
* `x(t)` 是输入数据。
* `α(t)` 是学习率，随着时间的推移而减小。

这个公式表明，BMU的权重向量会向输入数据移动，而相邻节点的权重向量会向BMU移动，形成一个拓扑结构。

# 3. SOM图像处理实践

### 3.1 SOM图像聚类

#### 3.1.1 SOM对图像数据的聚类

SOM图像聚类是一种基于SOM神经网络的图像处理技术，它可以将图像数据中的相似像素点聚类到一起，从而揭示图像中的内在结构和模式。

#### 3.1.2 SOM聚类结果的可视化

SOM聚类结果可以通过可视化方式呈现，例如：

* **U矩阵：**U矩阵是一个二维矩阵，其中每个元素表示一个SOM单元与相邻单元的距离。低值表示相邻单元相似，高值表示相邻单元不同。
* **特征映射：**特征映射是一个二维网格，其中每个单元表示一个SOM单元的权重向量。相邻单元的权重向量相似，形成不同的特征区域。

### 3.2 SOM图像降维

#### 3.2.1 SOM对图像数据的降维

SOM图像降维是一种利用SOM神经网络将高维图像数据降维到低维空间的技术。它可以保留图像数据的关键特征，同时减少数据量。

#### 3.2.2 SOM降维结果的应用

SOM降维结果可用于：

* **图像压缩：**通过降低图像数据的维数来实现图像压缩。
* **图像分类：**将降维后的图像数据输入分类器进行分类。
* **图像检索：**利用降维后的图像数据进行相似图像检索。

### 3.3 SOM图像处理实践代码示例

#### 3.3.1 SOM图像聚类代码

import numpy as np
import matplotlib.pyplot as plt
from minisom import MiniSom

# 加载图像数据
image = plt.imread('image.png')
image_data = image.reshape(image.shape[0] * image.shape[1], 3)

# 创建SOM网络
som = MiniSom(image.shape[0], image.shape[1], 3, sigma=1.0, learning_rate=0.5)

# 训练SOM网络
som.train(image_data, 1000)

# 可视化聚类结果
plt.imshow(som.distance_map().T, interpolation='nearest')
plt.colorbar()
plt.show()

#### 3.3.2 SOM图像降维代码

import numpy as np
from sklearn.decomposition import PCA

# 加载图像数据
image = plt.imread('image.png')
image_data = image.reshape(image.shape[0] * image.shape[1], 3)

# 使用SOM降维
som = MiniSom(10, 10, 3, sigma=1.0, learning_rate=0.5)
som.train(image_data, 1000)

# 使用PCA降维
pca = PCA(n_components=2)
pca_data = pca.fit_transform(image_data)

# 可视化降维结果
plt.scatter(pca_data[:, 0], pca_data[:, 1])
plt.show()

# 4. SOM图像处理进阶应用

### 4.1 SOM图像分割

#### 4.1.1 SOM在图像分割中的应用

SOM图像分割是一种基于自组织映射的神经网络技术，用于将图像分割成不同的区域或对象。它利用SOM网络的非监督学习能力，将图像中的像素映射到低维空间中，从而揭示图像中的潜在结构。

#### 4.1.2 SOM图像分割算法的实现

SOM图像分割算法的实现步骤如下：

1. **数据预处理：**将图像转换为灰度图像，并归一化像素值。
2. **SOM网络初始化：**创建具有特定拓扑结构（通常为矩形或六边形网格）的SOM网络。
3. **学习过程：**对图像中的每个像素进行迭代，将其分配给最相似的SOM神经元。
4. **权重更新：**更新与分配像素相关的SOM神经元的权重，使其更接近该像素。
5. **拓扑映射：**将SOM神经元映射到二维空间，以可视化图像中的潜在结构。
6. **分割：**使用聚类算法或阈值分割技术将SOM神经元分组为不同的区域。

### 4.2 SOM图像识别

#### 4.2.1 SOM在图像识别中的应用

SOM图像识别是一种利用SOM网络将图像分类为不同类别的技术。它通过将图像中的特征映射到低维空间中，从而提取图像的显著特征。

#### 4.2.2 SOM图像识别算法的实现

SOM图像识别算法的实现步骤如下：

1. **特征提取：**从图像中提取特征，例如颜色直方图、纹理特征或边缘检测结果。
2. **SOM网络初始化：**创建具有特定拓扑结构的SOM网络。
3. **学习过程：**对提取的特征进行迭代，将其分配给最相似的SOM神经元。
4. **权重更新：**更新与分配特征相关的SOM神经元的权重，使其更接近该特征。
5. **拓扑映射：**将SOM神经元映射到二维空间，以可视化图像的特征分布。
6. **分类：**使用聚类算法或最近邻分类器将SOM神经元分组为不同的类别。

### 代码示例：SOM图像分割

import numpy as np
import matplotlib.pyplot as plt
from minisom import MiniSom

# 加载图像并转换为灰度
image = plt.imread('image.jpg')
gray_image = np.mean(image, axis=2)

# 归一化像素值
gray_image = gray_image / 255.0

# 创建SOM网络
som = MiniSom(x=10, y=10, input_len=gray_image.shape[0] * gray_image.shape[1])

# 初始化SOM网络
som.random_weights_init(gray_image)

# 训练SOM网络
som.train_random(gray_image, 1000, verbose=True)

# 映射SOM神经元
som_map = som.distance_map().T

# 可视化SOM映射
plt.imshow(som_map, interpolation='nearest')
plt.show()

# 分割图像
segmented_image = np.zeros_like(gray_image)
for i in range(gray_image.shape[0]):
    for j in range(gray_image.shape[1]):
        segmented_image[i, j] = som.winner(gray_image[i, j])[0]

# 可视化分割结果
plt.imshow(segmented_image, interpolation='nearest')
plt.show()

**代码逻辑分析：**

* 该代码使用`minisom`库实现了SOM图像分割。
* `MiniSom`类用于创建和训练SOM网络。
* `random_weights_init`方法用于随机初始化SOM网络的权重。
* `train_random`方法用于训练SOM网络，使用随机像素顺序。
* `distance_map`方法返回SOM神经元之间的距离映射。
* `winner`方法返回与给定输入像素最相似的SOM神经元。
* 分割图像的循环将每个像素分配给最相似的SOM神经元，从而形成分割结果。

# 5.1 SOM在图像处理中的未来发展

### 5.1.1 SOM算法的改进和优化

随着计算机技术的不断发展，SOM算法也在不断地改进和优化。主要集中在以下几个方面：

- **学习率的优化：**学习率是SOM算法中一个重要的参数，它控制着权重的更新速度。传统的SOM算法使用固定学习率，但这种方法并不能很好地适应不同的数据集。因此，自适应学习率算法被提出，它可以根据数据集的特性动态调整学习率。
- **邻域函数的改进：**邻域函数定义了权重更新的范围。传统的SOM算法使用高斯邻域函数，但这种函数在边缘区域会出现权重更新不充分的问题。因此，提出了各种改进的邻域函数，如双曲余弦邻域函数和分段线性邻域函数，以解决边缘区域的权重更新问题。
- **权重初始化策略的优化：**权重初始化策略影响着SOM算法的收敛速度和最终的聚类结果。传统的SOM算法使用随机权重初始化，但这种方法可能会导致收敛速度慢和聚类结果不稳定。因此，提出了各种改进的权重初始化策略，如基于数据分布的权重初始化和基于K-means算法的权重初始化，以提高SOM算法的收敛速度和聚类结果的稳定性。

### 5.1.2 SOM在其他图像处理领域的应用

除了在图像聚类、降维、分割和识别等领域，SOM算法还在其他图像处理领域有着广泛的应用前景。

- **图像超分辨率：**SOM算法可以用于图像超分辨率，即从低分辨率图像中恢复高分辨率图像。通过将低分辨率图像映射到SOM网格，并使用网格中的权重对低分辨率图像进行插值，可以得到高分辨率图像。
- **图像去噪：**SOM算法可以用于图像去噪，即从噪声图像中恢复干净图像。通过将噪声图像映射到SOM网格，并使用网格中的权重对噪声图像进行滤波，可以得到干净图像。
- **图像增强：**SOM算法可以用于图像增强，即改善图像的视觉效果。通过将图像映射到SOM网格，并使用网格中的权重对图像进行调整，可以得到增强后的图像。