生物信息学中的自组织映射（SOM）：探索基因和疾病的奥秘

# 1. 自组织映射（SOM）简介

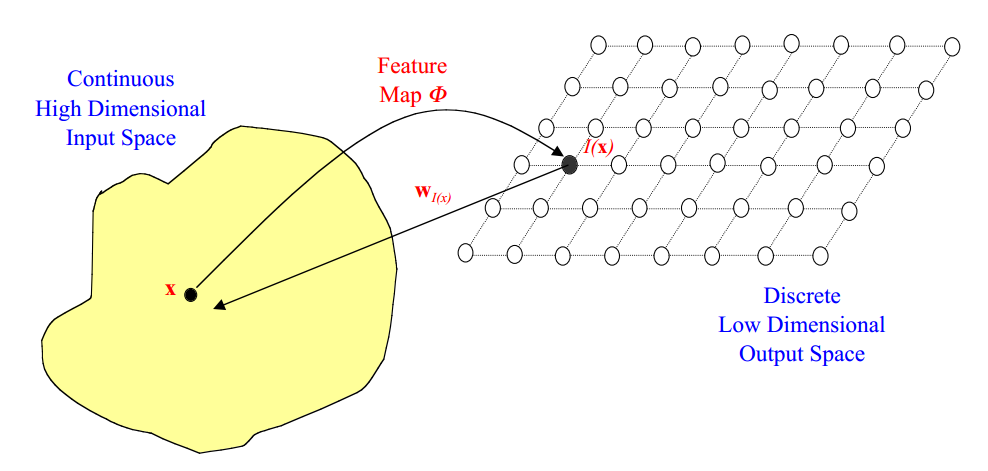
自组织映射（SOM）是一种非监督学习算法，它可以将高维数据映射到低维空间中，同时保持输入数据的拓扑结构。SOM的灵感来自于人类大脑中神经元的自组织特性，它通过竞争性学习和拓扑保持两个机制来实现自组织。

SOM算法首先将输入数据随机初始化为一组权重向量，这些权重向量位于低维空间中。然后，算法迭代地将输入数据与权重向量进行比较，并选择与输入数据最相似的权重向量。选定的权重向量及其邻域中的权重向量将向输入数据更新，从而使它们更接近输入数据。通过这种方式，SOM算法可以将高维输入数据映射到低维空间中，同时保持输入数据的拓扑结构。

# 2. SOM在生物信息学中的理论基础

### 2.1 SOM的算法原理

#### 2.1.1 竞争性学习

SOM算法的核心思想是竞争性学习，即在训练过程中，神经元之间会竞争成为输入数据的最佳匹配。具体而言，算法会为每个神经元分配一个权重向量，该向量与输入数据具有相同的维度。在训练过程中，算法会将输入数据与每个神经元的权重向量进行比较，并选择最相似的神经元作为获胜神经元。

#### 2.1.2 拓扑保持

拓扑保持是SOM算法的另一个关键特征，它确保了获胜神经元在输出空间中的位置与输入数据在输入空间中的位置保持拓扑关系。为了实现拓扑保持，算法会使用邻域函数，该函数定义了获胜神经元周围神经元的激活程度。邻域函数通常是高斯函数或墨西哥帽函数，其值随着与获胜神经元的距离而减小。

### 2.2 SOM的数学模型

#### 2.2.1 权重向量的更新规则

SOM算法的权重向量的更新规则如下：

w_i(t+1) = w_i(t) + α(t) * (x(t) - w_i(t)) * h_ij(t)

其中：

* `w_i(t)`是神经元`i`在时间`t`的权重向量
* `x(t)`是输入数据
* `α(t)`是学习率，随着训练的进行而减小
* `h_ij(t)`是神经元`i`和获胜神经元`j`之间的邻域函数

#### 2.2.2 邻域函数

邻域函数定义了获胜神经元周围神经元的激活程度。常用的邻域函数有：

* 高斯函数：`h_ij(t) = exp(-||r_i - r_j||^2 / (2σ^2(t)))`
* 墨西哥帽函数：`h_ij(t) = exp(-||r_i - r_j||^2 / (2σ^2(t))) - exp(-||r_i - r_j||^2 / (2σ^2(t)))`

其中：

* `r_i`和`r_j`分别是神经元`i`和`j`的位置
* `σ(t)`是邻域函数的宽度，随着训练的进行而减小

# 3. SOM在生物信息学中的实践应用

### 3.1 基因表达谱数据的聚类

#### 3.1.1 SOM用于基因表达谱数据的降维

基因表达谱数据通常包含大量基因的表达水平信息，维度很高。为了便于分析，需要对数据进行降维。SOM是一种非线性降维算法，可以将高维数据映射到低维空间中，同时保持数据的拓扑结构。

**代码块：**