降维中的自组织映射（SOM）：复杂数据的简化之道

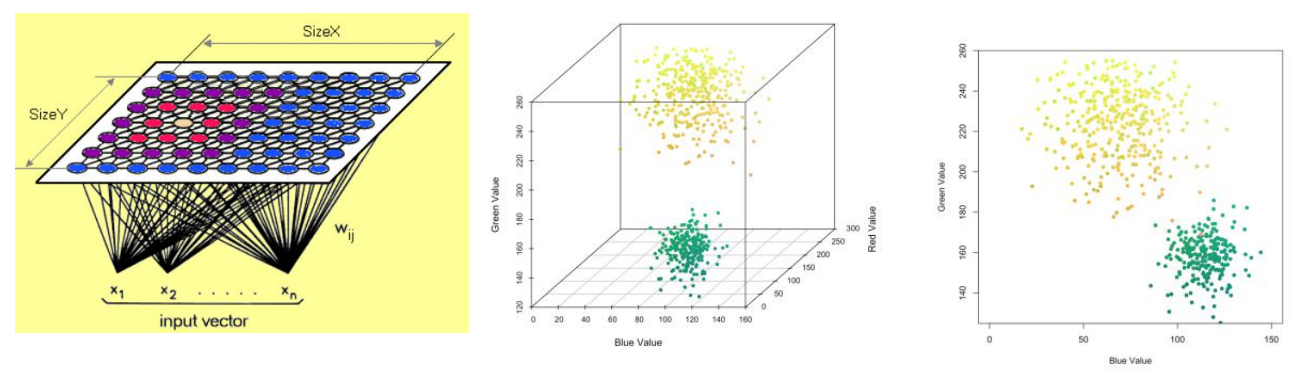
# 1. 自组织映射（SOM）简介**

自组织映射（SOM），又称科洪能图（Kohonen Map），是一种无监督机器学习算法，用于将高维数据映射到低维空间，从而实现数据的可视化、降维和聚类。

SOM算法的核心思想是竞争学习和拓扑结构保持。通过竞争学习，SOM将输入数据分配到最相似的输出节点（神经元）上。拓扑结构保持确保了相邻输入数据在输出空间中也保持相邻关系，从而保留了数据的拓扑结构。

SOM的优势在于其能够将复杂的高维数据映射到低维空间，同时保持数据的拓扑关系。这使得SOM在数据可视化、聚类分析和降维方面具有广泛的应用，例如图像处理、自然语言处理和时间序列分析。

# 2. SOM的理论基础

### 2.1 SOM的算法原理

自组织映射（SOM）是一种无监督学习算法，它通过将高维数据映射到低维空间（通常是二维或三维）来实现降维。SOM算法的核心思想是竞争学习和拓扑结构保持。

#### 2.1.1 竞争学习

竞争学习是一种神经网络学习规则，它通过竞争机制来确定每个神经元对输入模式的响应。在SOM中，每个神经元都与一个权重向量相关联，该权重向量表示神经元在输入空间中的位置。当一个输入模式被呈现给SOM时，与输入模式最相似的权重向量的神经元将成为获胜神经元。

#### 2.1.2 拓扑结构保持

拓扑结构保持是指SOM中的神经元在输入空间中的位置与它们在低维输出空间中的位置之间存在拓扑关系。这意味着相邻的神经元在输入空间中也应该是相邻的。SOM算法通过使用邻域函数来实现拓扑结构保持。邻域函数定义了获胜神经元周围神经元的影响范围。

### 2.2 SOM的数学模型

SOM的数学模型可以表示为：

# 权重更新规则
w_ij(t+1) = w_ij(t) + α(t) * h_ij(t) * (x_i(t) - w_ij(t))

# 距离度量
d_ij = ||x_i - w_ij||^2

# 邻域函数
h_ij(t) = exp(-d_ij / (2 * σ^2(t)))

其中：

* `w_ij` 是神经元 `j` 在输入空间中第 `i` 个维度上的权重
* `x_i` 是输入模式的第 `i` 个维度
* `α(t)` 是学习率
* `h_ij(t)` 是邻域函数
* `σ(t)` 是邻域函数的标准差

**距离度量**：`d_ij` 使用欧几里德距离来度量输入模式 `x_i` 和神经元 `j` 之间的距离。

**邻域函数**：`h_ij(t)` 是一个高斯函数，它定义了获胜神经元周围神经元的影响范围。随着时间推移，邻域函数的标准差 `σ(t)` 会逐渐减小，从而减少邻域的影响范围。

**权重更新规则**：权重更新规则使用竞争学习和拓扑结构保持的原则来更新神经元的权重。获胜神经元及其邻域中的神经元将向输入模式移动，而其他神经元的权重将保持不变。

# 3.1 数据可视化

自组织映射（SOM）在数据可视化方面有着广泛的应用，它可以将高维数据投影到低维空间中，从而方便人们直观地理解数据的分布和结构。

#### 3.1.1 U-Matrix

U-Matrix（统一距离矩阵）是一种可视化SOM拓扑结构的方法。它将SOM中的每个神经元与相邻神经元之间的距离以矩阵的形式表示出来，其中距离越小，神经元之间的连接越紧密。

import numpy as np
import matplotlib.pyplot as plt

# 创建一个SOM
som = SOM(10, 10)

# 训练SOM
som.train(data)

# 计算U-Matrix
u_matrix = som.get_u_matrix()

# 可视化U-Matrix
plt.imshow(u_matrix, cmap='hot')
plt.colorbar()
plt.show()

**逻辑分析：**

* `get_u_matrix()`方法计算了SOM中每个神经元与相邻神经元之间的距离。
* `imshow()`函数将U-