数据挖掘中的自组织映射（SOM）：挖掘数据背后的宝藏

# 1. 自组织映射（SOM）简介**

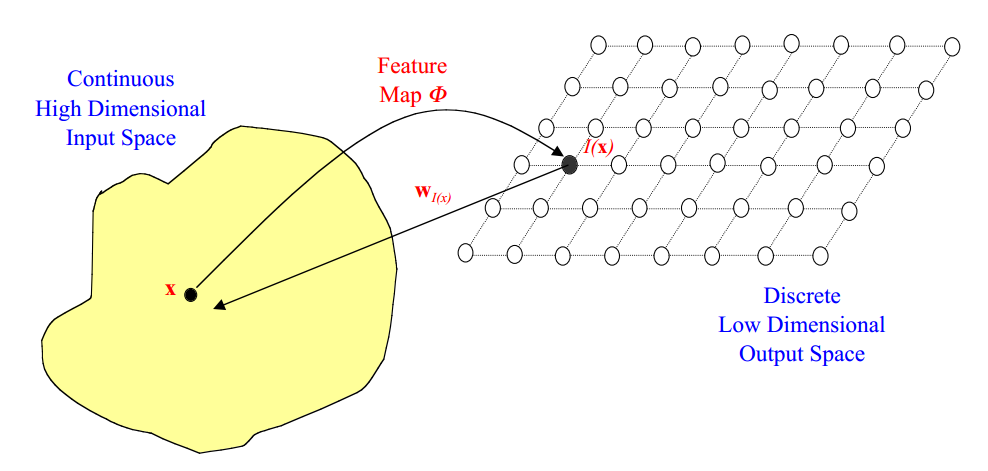
自组织映射（SOM）是一种无监督神经网络算法，它能够将高维数据映射到低维空间，同时保留输入数据的拓扑结构。SOM的独特之处在于其自组织特性，它可以自动发现数据中的模式和关系，而无需人工干预。

SOM算法最初由芬兰神经科学家Teuvo Kohonen于1982年提出。它是一种非线性投影算法，能够将高维输入数据映射到低维输出空间，通常为二维或三维。SOM网络由一个神经元阵列组成，每个神经元都与输入数据中的一个特征向量相关联。

# 2. SOM算法原理**

**2.1 SOM神经网络结构**

自组织映射（SOM）神经网络是一种非监督学习算法，其结构类似于生物神经网络。SOM网络由一个二维网格状的节点组成，每个节点都与一个权重向量相关联。权重向量的大小与输入数据的维度相同。

**2.2 SOM学习算法**

SOM学习算法是一个迭代过程，包括以下三个主要步骤：

**2.2.1 初始化**

1. 随机初始化每个节点的权重向量。
2. 设置学习率α和邻域半径σ。

**2.2.2 竞争学习**

1. 从训练数据中随机选择一个输入向量x。
2. 对于网络中的每个节点i，计算节点权重向量wi与输入向量x之间的欧氏距离。
3. 找到与x距离最小的节点，称为获胜节点。

**2.2.3 权重更新**

1. 更新获胜节点及其邻域内节点的权重向量：

w_i(t+1) = w_i(t) + α(t) * (x(t) - w_i(t))

其中：

* t表示当前迭代次数
* α(t)是学习率，随时间衰减
* σ(t)是邻域半径，随时间衰减

2. 邻域内的节点权重更新幅度随着与获胜节点的距离而减小。

**代码块：**

import numpy as np

class SOM:
    def __init__(self, input_dim, map_size, learning_rate=0.1, radius=1):
        self.input_dim = input_dim
        self.map_size = map_size
        self.weights = np.random.rand(map_size[0], map_size[1], input_dim)
        self.learning_rate = learning_rate
        self.radius = radius

    def train(self, data, epochs=100):
        for epoch in range(epochs):
            for x in data:
                # 竞争学习
                winner = np.argmin(np.linalg.norm(self.weights - x, axis=2))
                winner_row, winner_col = winner // self.map_size[1], winner % self.map_size[1]

                # 权重更新
                for i in range(self.map_size[0]):
                    for j in range(self.map_size[1]):
                        distance = np.linalg.norm([i - winner_row, j - winner_col])
                        if distance <= self.radius:
                            self.weights[i, j] += self.learning_rate * (x - self.weights[i, j])

                # 学习率和邻域半径衰减
                self.learning_rate *= 0.9
                self.radius *= 0.9

**逻辑分析：**

* `__init__`方法初始化SOM网络，包括权重、学习率和邻域半径。
* `train`方法对数据进行训练，包括竞争学习和权重更新。
* 竞争学习通过计算输入向量与每个节点权重向