Python回溯算法入门：解决难题的分步策略

# 1. Python回溯算法简介

回溯算法是一种通过探索所有可能情况来找到所有解的算法，它在求解组合问题时表现出色，如排列、组合以及图论中的各种路径问题。Python由于其简洁的语法和强大的标准库支持，成为实现回溯算法的理想选择。本章将简单介绍回溯算法及其在Python中的应用，为后续章节的深入讨论和实战应用打下基础。

在开始之前，了解回溯算法的简单应用将帮助我们更好地理解它的工作原理。下面通过一个简单的例子来说明回溯算法的流程：

# Python示例：八皇后问题的简单回溯解法
def is_safe(board, row, col):
    # 检查当前列是否安全
    for i in range(row):
        if board[i] == col or \
           board[i] - i == col - row or \
           board[i] + i == col + row:
            return False
    return True

def solve_n_queens(board, row):
    if row >= len(board):
        return True
    for col in range(len(board)):
        if is_safe(board, row, col):
            board[row] = col
            if solve_n_queens(board, row + 1):
                return True
            board[row] = -1
    return False

def print_solution(board):
    print(["." * i + "Q" + "." * (len(board) - i - 1) for i in board])

# 用-1表示空列
board = [-1] * 8
if solve_n_queens(board, 0):
    print_solution(board)

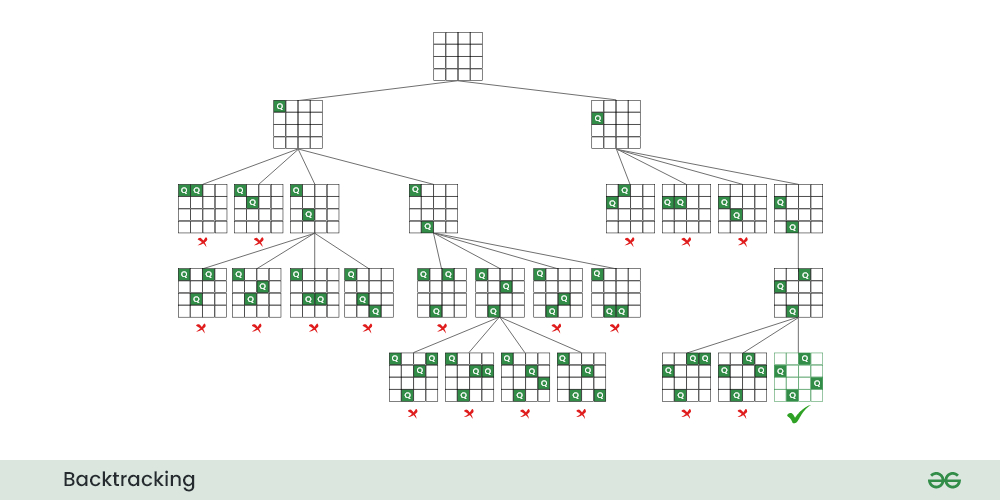
上述代码展示了如何使用回溯算法解决经典的八皇后问题。八皇后问题要求在8x8的棋盘上放置8个皇后，使得它们不能相互攻击，即任意两个皇后都不能处于同一行、同一列或同一对角线上。代码中定义了递归函数`solve_n_queens`来尝试每一种可能的放置方法，并在找到解决方案时返回True，从而触发回溯。通过这个例子，我们可以看到回溯算法在解决组合问题时的基本逻辑：尝试每一种可能，并在不满足条件时返回前一步进行新的尝试。

# 2. 回溯算法理论基础

## 2.1 回溯算法概念与特点

### 2.1.1 算法定义

回溯算法是一类重要的算法思想，主要用于解决多阶段决策问题，其核心是尝试-回溯的过程。在每一个决策点上，算法尝试每一种可能的决策，并递归地进入下一决策过程。如果当前决策导致问题无解，则算法会回退到上一个决策点，尝试另一种可能的决策。这种策略可以系统地搜索出所有可能的候选解，并从中筛选出满足条件的解。

### 2.1.2 算法特性

回溯算法具有以下特点：

- **全局性**：算法尝试所有可能的解决方案，以找到满足约束条件的最优解或可行解。
- **递归性**：算法通常以递归的形式实现，通过递归调用自身来实现决策的深入和回溯。
- **试探性**：算法在决策过程中进行试探，一旦发现当前路径不可能产生有效解，则回退到上一步。
- **剪枝性**：通过剪枝操作，算法能有效避免搜索不必要的分支，从而提高效率。

## 2.2 回溯算法的数学模型

### 2.2.1 状态空间树

状态空间树是回溯算法中用于描述问题搜索空间的一种树状结构。每个节点代表问题的一个状态，节点之间的连线代表可能的决策动作。在搜索过程中，算法从根节点开始，沿着树的深度方向探索，直至找到目标状态或所有状态探索完毕。

### 2.2.2 剪枝策略

剪枝是回溯算法中提高搜索效率的关键技术。它通过对状态空间树的某些节点或分支进行分析和判断，确定哪些分支不可能产生解或不是最优解，从而提前终止这部分搜索，避免无谓的计算。

#### 举例说明剪枝策略

考虑一个简单的组合问题，目标是从1到10中选择数字的组合，使得和为特定值。使用剪枝策略可以避免无效搜索：

def is_useful(combination, target):
    # 如果当前组合的和已经超过目标值，剪枝
    return sum(combination) <= target

# 使用回溯搜索
def search_combinations(numbers, target, start, combination):
    if is_useful(combination, target):
        # 剪枝
        return
    # 其他逻辑...

在这段代码中，`is_useful`函数作为剪枝函数，它能提前判断当前组合是否有可能达到目标和，如果不可能，则直接回溯，不继续搜索。

## 2.3 回溯算法的框架结构

### 2.3.1 递归函数的构建

回溯算法通常使用递归函数来实现。递归函数在每个决策点调用自身，并传递不同的参数来代表不同的决策状态。递归函数的基本结构包括：

- 递归终止条件：当达到某个决策点时，检查是否满足约束条件，如果满足则返回成功，否则回溯。
- 递归逻辑：在递归函数内部，通常需要进行状态更新，并遍历所有可能的决策，对于每一个决策调用递归函数自身。

### 2.3.2 全局与局部变量的管理

在实现回溯算法时，需要合理管理全局变量和局部变量。全局变量通常用于存储全局状态，比如当前解、最优解等；局部变量用于表示当前递归层次的状态。正确使用和更新这些变量对于确保算法正确性和效率至关重要。

# 全局变量，用于存储当前解和最优解
current_solution = []
best_solution = []

# 递归函数中使用局部变量来存储当前决策状态
def backtrack(level, options):
    if level == len(options):
        # 到达递归终点，检查当前解是否为最优解
        if is_better(current_solution, best_solution):
            best_solution = current_solution.copy()
        return
    for option in options[level]:
        # 做出决策
        current_solution.append(option)
        # 递归调用
        backtrack(level + 1, options)
        # 回溯，撤销决策
        current_solution.pop()

在上述代码中，`current_solution` 和 `best_solution` 作为全局变量，分别存储当前解和最优解。每次递归调用时，`level` 和 `options` 作为局部变量传递当前决策的层级和可用选项。回溯发生在每次递归返回时，需要撤销当前决策，以便探索其他可能的路径。

下一章节将介绍如何使用Python实现回溯算法及其优化，让我们进入更实际的应用场景中。

# 3. Python实现回溯算法

在掌握回溯算法的基础理论之后，我们即将进入实战演练阶段，使用Python语言来实现回溯算法。Python以其简洁的语法和强大的库支持，成为实现算法，尤其是高级算法的热门选择。在本章中，我们将探索Python在回溯算法实现中的应用，包括基础语法